
Интуиция, лежащая в основе мульти-токного прогноза: теория информации и точки выбора
11 июня 2025 г.Таблица ссылок
Аннотация и 1. Введение
2. Метод
3. Эксперименты по реальным данным
3.1. Шкала преимуществ с размером модели и 3,2. Более быстрый вывод
3.3. Изучение глобальных моделей с помощью мульти-байтового прогноза и 3.4. Поиск оптимальногоне
3.5. Обучение для нескольких эпох и 3.6. Создание нескольких предикторов
3.7 Многократный прогноз на естественном языке
4. Абляции на синтетических данных и 4.1. Индукционная способность
4.2. Алгоритмические рассуждения
5. Почему это работает? Некоторые спекуляции и 5.1. Lookahead Укрепляет очки выбора
5.2. Информация теоретичный аргумент
6. Связанная работа
7. Заключение, Заявление о воздействии, воздействие на окружающую среду, подтверждения и ссылки
A. Дополнительные результаты по самопрокативному декодированию
Б. Альтернативные архитектуры
C. Скорость тренировок
D. МАГАЗИН
E. Дополнительные результаты по поведению масштабирования модели
F. Подробности о CodeContests Manetuning
G. Дополнительные результаты по сравнению с естественным языком
H. Дополнительные результаты по абстрактному текстовому суммированию
I. Дополнительные результаты по математическим рассуждениям на естественном языке
J. Дополнительные результаты по индукционному обучению
K. Дополнительные результаты по алгоритмическим рассуждениям
L. Дополнительные интуиции по многоцелевым прогнозам
М. Обучение гиперпараметры
L. Дополнительные интуиции по многоцелевым прогнозам
L.1. Сравнение с запланированной выборкой
В разделе 5.2 мы утверждали, что многократный прогноз снижает несоответствие распределения между обучением, основанным на учителях, и ауторегрессивной оценкой языковых моделей. Запланированная выборка (Bengio et al., 2015) представляет собой метод обучения учебным планам, который также направлен на то, чтобы преодолеть этот разрыв в задачах прогнозирования последовательностей путем постепенной замены все больше и большего количества входных токенов на созданные модели.
Несмотря на эффективность в таких областях, как прогнозирование временных рядов, запланированная выборка, по нашему мнению, неприменима к языковому моделированию из -за дискретного характера текста. Замена входных последовательностей истины путем чередования основных истинных токенов часто приводит к неграмотному, фактически неправильному или иному бессвязному тексту, которого следует избегать любой ценой. Более того, в отличие от предсказания с несколькими точками, техника, первоначально разработанная для рецидивирующих нейронных сетей, не может быть легко адаптирована для параллельных тренировочных настройки, таких как модели трансформатора.
L.2. Информация теоретичный аргумент
Мы рассказываем о теоретичных терминах информации, появляющихся в разложении в разделе 5.2 и получаем относительную версию, которая аналогично позволяет разложить потери предсказания с несколькими точками. Как и в разделе 5.2, обозначите x следующим токеном и Y вторым, нуженным, и опустите кондиционирование в предыдущем контексте C для простоты обозначения. В разделе 5.2 мы разложились H (x) + H (y)-количество интереса для 2-то что-то-ток-моделей прогнозирования-как следует:
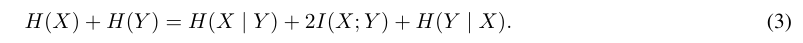
Давайте объясним каждый из терминов. Условия энтропии обозначают неопределенность, содержащуюся в случайных переменных и Y. [2] [2] [2]. Условная энтропия h (x | y) является более теоретической сущностью, не моделируемой причинными моделями. Он описывает неопределенность в отношении x, учитывая префикс C и суффикс Y, и, следовательно, отражает локальные вариации x, которые не влияют на продолжение текста Y. Взаимная информация I (x; Y), с другой стороны, описывает информацию о Y, содержащуюся в x (и наоборот) и, следовательно, захватывает вариации x, которая ограничивает продолжение текста.
Тем не менее, аргумент, приведенный в разделе 5.2, зависит от предположения о том, что потери с несколькими точками подчиняются аналогичному разложению, что и сумма самих энтропий с истинной территорией. Давайте сделаем это строгим. ОбозначайтеP (x, y)совместное распределениеХиУ, кP (x)(коротко дляpx (x))предельное распределение X иP (y) один из Y. Обозначает плотность прогнозов моделиQ (x, y), Q (x)иQ (Y)соответственно, условные распределенияP (x | y)и Kullback-Leibler Divergence отQ.кпкD (с ∥ Q)и перекрестная энтропия от Q к P от H (P, Q).
Определение L.1.Условная перекрестная энтропияH (px | y, qx | y)изХобусловлено y отQ.кпопределяется как ожидание в рамках y перекрестной энтропии между распределениямипкиQXобусловлено Y, в формулах:
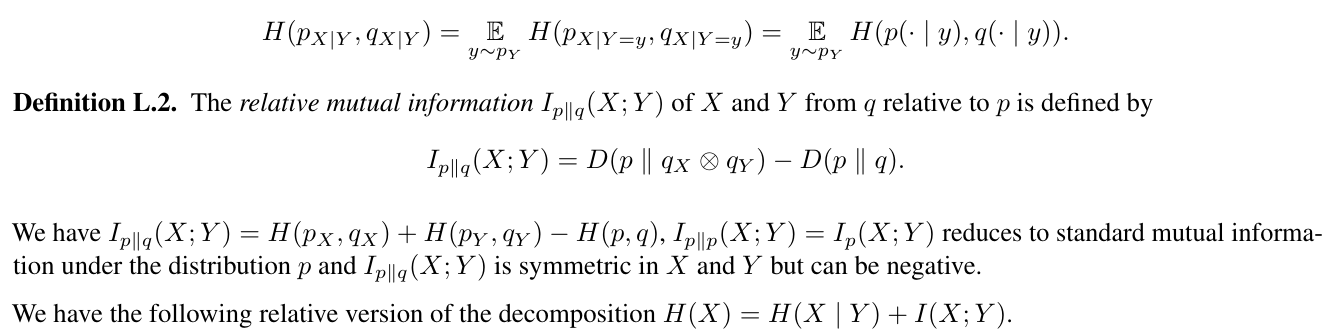
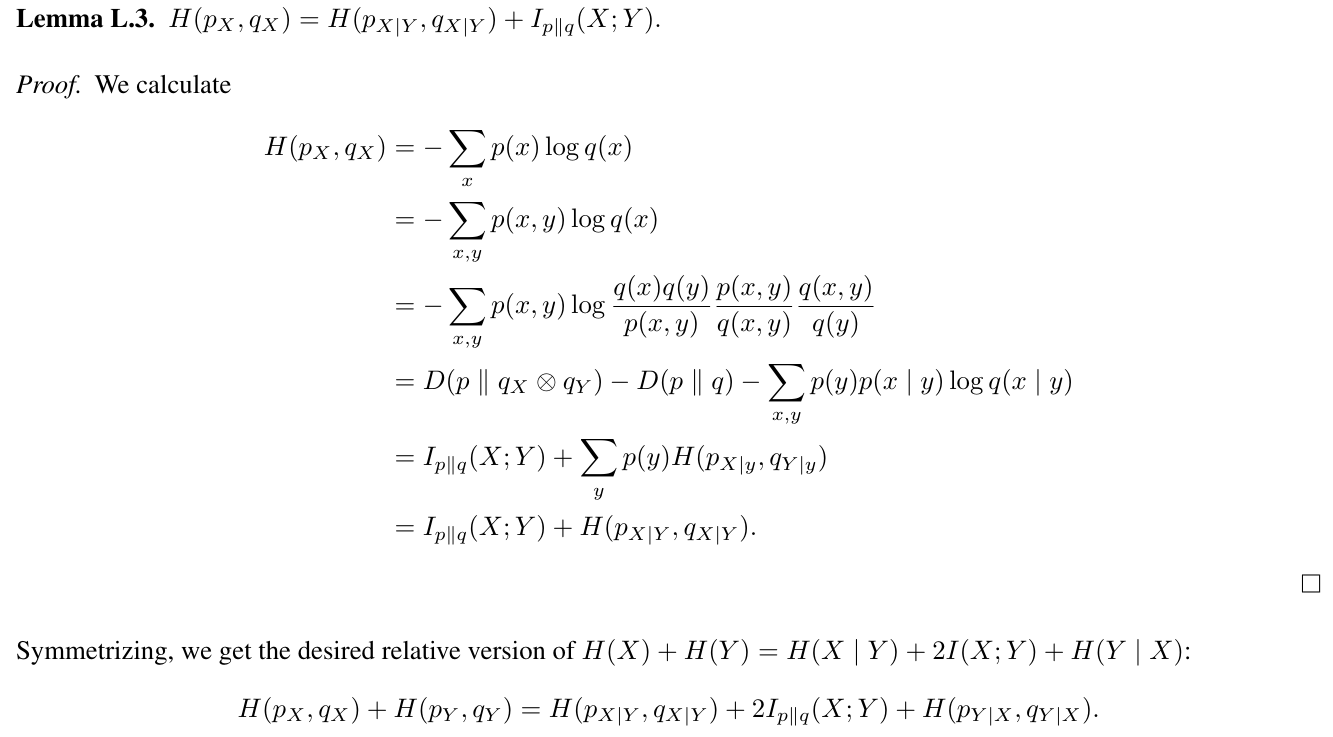
Установка P для эмпирического распределения учебных данных, левая сторона описывает потери перекрестной энтропии, используемые для обучения 2-то-ток-моделей прогнозирования. Правая сторона придает разложение в локальный термин перекрестной энтропии, термин взаимной информации с весом два и сдвинутый термин следующего точки. Мы интерпретируем это следующим образом: добавив термин H (PY, QY) в потерю, 2-Token Prediction стимулирует модели для предварительного выпуска, которые станут полезными для прогнозирования Y на следующем этапе и увеличивает вес относительного взаимной информации в потере. Что на самом деле означает относительная взаимная информация? Интерпретируя дивергенцию kullback-leibler d (p ∥ q) как среднее количество битов, необходимых в дополнение к отправке данных из P с кодом, оптимизированным для Q вместо P, мы видим, что минимизация
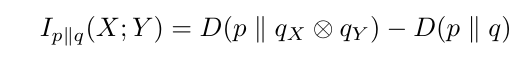
означает минимизация среднего количества дополнительных бит, необходимых для отправки данных из P с кодом, оптимизированным для Q, который рассматривает X и Y как независимые по сравнению с тем, что нет. Если это число невелико, Q удалось использовать взаимную информацию X и Y под p.
L.3. Lookahead Укрепляет очки выбора
Обучение с мульти-головным прогнозом увеличивает важность выбора точек в потере по сравнению с несущественными решениями. Чтобы сделать этот аргумент, мы представляем упрощенную модель языкового моделирования. Рассмотрим задачу последовательного решения и модель M, которая обучена учителям, основанным на оптимальных траекториях. Мы различаем точки выбора - трансляции, которые приводят к различным результатам - и несущественные решения, которые этого не делают (рис. S17 (a) и (b)).
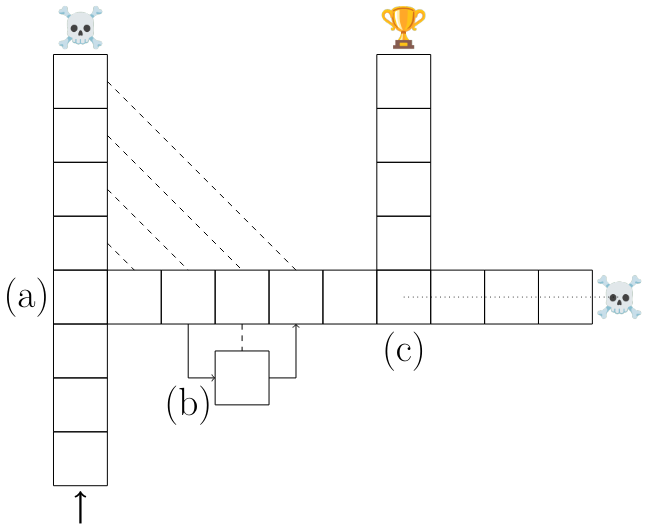

Как утверждалось в разделе 5.1, мы считаем, что эта модель отражает важные особенности обучения и вывода с языковыми моделями: точки выбора являются семантически важными поворотными точками в сгенерированных текстах, такие как окончательный ответ на вопрос или конкретная строка кода, в то время как несущественные решения могут быть выбором среди синонимов или переменных имен в коде.

L.4. Заказы факторизации
Хотя продвижение вперед во времени, безусловно, является наиболее естественным выбором порядка факторизации, существуют случаи, когда он является неоптимальным. Например, в языках инфлексии, согласие между связанными частями предложения является частым шаблоном с одним словом, направляющим грамматические формы других. Рассмотрим немецкий предложение
Wie Konnten Auch Worte Meiner Durstenden Seele Genügen? [3]
Фридрих Хёлдерлин, фрагмент фон -гиперион (1793)
В тех случаях, когда «Genügen» требует объекта Dative Case, а затем «Seele» требует, чтобы притяжательное местоимение «Mein» было в женской единственной дативной форме «Myiner» и причастие «durstend», чтобы быть в женской единственной дательской форме в слабом склоне «Дерстенден», потому что он следует за «Myiner». Другими словами, порядок факторизации
Wie Konnten Auch Worte → Genügen → Seele → Meiner → Durstenden?
Возможно, это легче для построения вышеуказанного предложения. Таким образом, люди, а также языковые модели должны выполнять эту факторизацию (которая отклоняется от причинного порядка, в котором происходят прогнозы!) В рамках их скрытых активаций, и 4-торальная потеря прогнозирования облегчает это, поскольку явно поощряет модели иметь всю информацию о последующих 4 токенах в своих скрытых представлениях.
Эта статья естьДоступно на ArxivПод CC по лицензии 4.0.
[2] В частности, они не относятся кмодельпрогнозы.
[3] грубо:Как слова могут быть достаточно для моей жаждущей души?
Авторы:
(1) Фабиан Глокл, ярмарка в Meta, Cermics Ecole des Ponts Paristech и внес свой вклад;
(2) Badr Youbi Idrissifair в Meta, Lisn Université Paris-Saclay и внес свой вклад;
(3) Baptiste Rozière, ярмарка в Meta;
(4) Дэвид Лопес-Паз, ярмарка в Мете и его последний автор;
(5) Габриэль Синнев, ярмарка в Meta и последний автор.
Оригинал

