
Как обойти ошибку целочисленного деления в смарт-контрактах
20 февраля 2023 г.Мы все слышали о числах с плавающей запятой в школе. В отличие от целых чисел без десятичной точки.
Не нужно быть гением математики, чтобы знать, что число пять является целым числом, а 5,43 — числом с плавающей запятой. Ясно, что мы все знакомы с десятичной точкой, которая является четкой точкой различия между ними.
Конечно, неудивительно, что числа с плавающей запятой используются в языках программирования и даже классифицируются как отдельный примитивный тип данных из-за того, насколько они необходимы для повседневных вычислений.
Использование чисел с плавающей запятой в языках программирования
Когда вы начнете изучать Python или Java, вы будете использовать тип данных float. В частности, когда вы сами выполняете операцию деления между двумя числами с плавающей запятой.
В Python, даже если вам не нужно объявлять число с плавающей запятой, деление двух таких чисел может привести к числу одного и того же типа данных, как показано ниже:

Мы можем получить тот же результат и в Java, даже если нам придется явно объявить примитивный тип данных «плавающий» для всех используемых переменных.

Как можно заметить, такого рода вычисления необходимы для ряда приложений, и именно поэтому операции с числами с плавающей запятой доступны как функция в обоих этих языках программирования.
С другой стороны, если вы изучали Solidity, вы должны были заметить, что он не включает тип данных числа с плавающей запятой.
Как Solidity выполняет транзакции без использования чисел с плавающей запятой
Вместо этого, если вы написали какой-либо код в Solidity, вы должны использовать числа либо со знаком, либо без знака целочисленного типа.
Итак, если вы хотите выполнить те же вычисления — пять разделить на два — как показано в предыдущем разделе, вот как это будет выглядеть в рамках смарт-контракта:

Однако результат, который вы получите, будет другим, так как Solidity не поддерживает тип данных float. По крайней мере, пока.
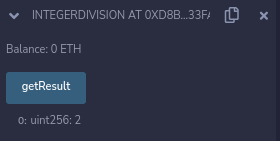
В частности, Solidity округлит результат до нуля. Что в данном случае, как показано выше, приведет к значению два. Думайте об этом как об операции по модулю над обоими числами.
Хотя в обычных обстоятельствах это не должно иметь большого значения, бывают случаи, когда результат может привести к ошибке в вычислениях. Вот почему рекомендуется по возможности избегать или откладывать операцию деления.
Ваш первый взгляд на ошибку целочисленного деления
Даже если школьное правило BODMAS требует, чтобы все учащиеся-математики выполняли вычисления деления перед умножением, это не рекомендуется, если вам нужно выполнить целочисленное деление в Solidity.
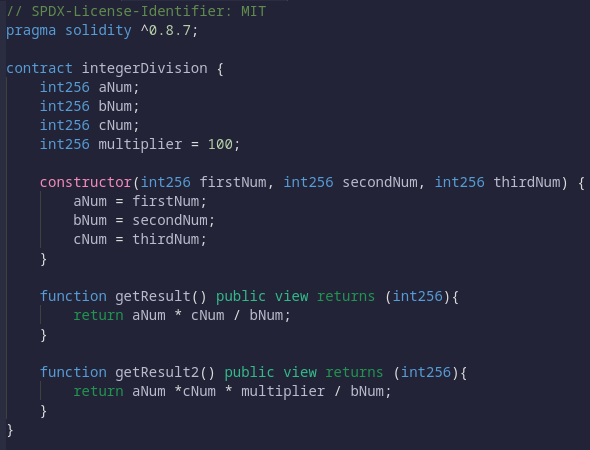
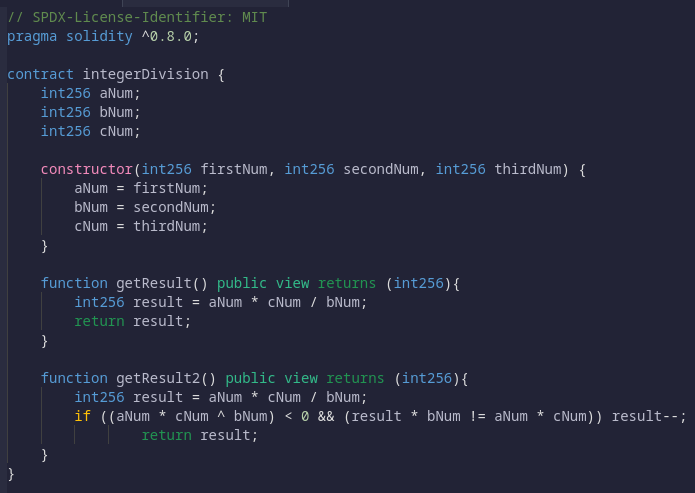
Давайте выясним, почему на этом простом примере выполняется умножение и деление трех чисел:
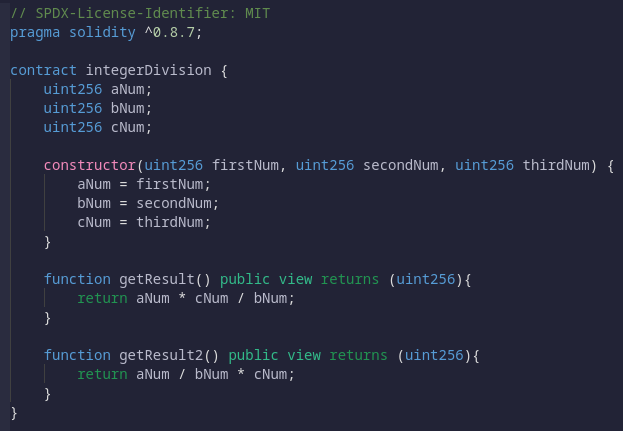
Если вы введете числа один, три и пять при развертывании смарт-контракта, вы должны получить одинаковое значение для функций getResult и getResult2, верно?
Если вы используете простой калькулятор, вы должны получить значение с плавающей запятой 1,666, что соответствует единице в Solidity, благодаря отсутствию значений с плавающей запятой.
К сожалению, этого не происходит, когда вы проверяете результаты функций getResult и getResult2, как показано ниже:
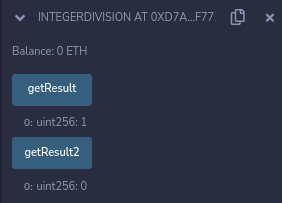
Если мы сначала выполним деление, мы получим окончательный результат, равный нулю. В отличие от ожидаемого значения единицы, когда вы откладываете эту операцию до конца в функции getResult.
Как вы можете заметить, даже если мы вычислили это значение, предвидя отсутствие значений с плавающей запятой, все равно возникает ошибка, которая может привести к потере точности. Что, в свою очередь, может привести к экономическим потерям, которые можно легко обойти.
Итак, как нам предотвратить ошибку целочисленного деления? Что еще более важно, как мы можем повысить точность наших вычислений? Давайте узнаем три наиболее распространенных способа сделать это.
3 способа предотвратить ошибку целочисленного деления
Учитывая, что существует несколько подходов к обходу этой ошибки, давайте начнем с самого простого исправления и рассмотрим еще несколько, прежде чем на этом закончить.
Способ 1. Используйте множитель
Теперь, наряду с размещением операции деления на последнем месте, одним из способов гарантировать, что вы не получите ошибок или неточных значений, является использование множителя. В приведенном ниже примере мы будем использовать множитель 100 вместе с теми же тремя числами, которые использовались ранее.
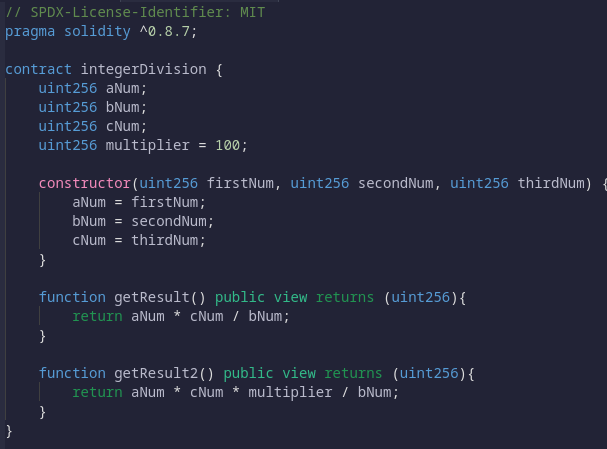
Теперь, когда вы развернете контракт со следующим кодом и вызовете обе функции, вы получите следующий результат:
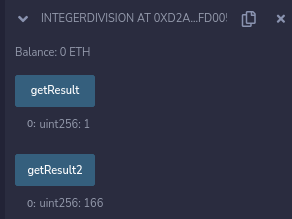
Поскольку желаемый результат — 1,666 или 166/100, мы видим, что значение getResult2 обеспечивает необходимую точность, когда множитель работает в сочетании с тремя числами. Конечно, если вы не используете множитель, как в функции getResult, вы получите 1.
Где 0,666 усекается от результата, как и ожидается по умолчанию при использовании Solidity. Итак, чтобы получить это значение, все, что вам нужно сделать, это разделить результат на множитель.
Как вы, возможно, знаете, Solidity приближается к нулю, когда дело доходит до округления как в случае целых чисел со знаком, так и в случае целых чисел без знака, поэтому это исправление работает и в случае целых чисел со знаком, как только вы развернете и запустите приведенный ниже код с аргументами минус один. , три и пять:
Что касается значений, сгенерированных функциями для целых чисел со знаком, то вот они:
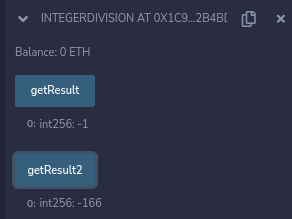
Ясно, что мы можем поддерживать точность и для целых чисел со знаком, используя множитель. Хотя существует точный способ округления целых чисел со знаком, который мы рассмотрим далее.
Способ № 2. Используйте деление пола для целых чисел со знаком
Теперь, если посмотреть на числовую строку ниже, результат выполнения целочисленного деления между двумя целыми числами без знака округляется ближе к нулю. Как и в случае получения 1,666, Solidity округляет его до 1, что является меньшим числом.
Однако, когда речь идет о целых числах со знаком, результат -1,6666 будет округлен до -1, который является большим из двух чисел. Таким образом, здесь должно применяться деление по полу, а не деление с округлением до нуля, которое реализовано в Solidity по умолчанию. Ради точности, конечно.
Если бы был доступен тип данных с плавающей запятой, было бы вычислено значение -1,666. В то время как Solidity округляет это значение до -1, применение деления пола к целым числам со знаком уменьшит его до -2.
Когда вы вызываете функции getResult и getResult2, мы получаем значение, как показано ниже, для аргументов минус один, три & пять:
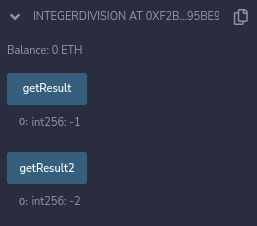
Как вы можете заметить, getResult вычисляет значение, используя метод округления до нуля, в то время как getResult2 округляет его до наименьшего целого числа в силу деления пола.
Способ 3. Используйте библиотеку ABDKMath64x64
Теперь, в качестве последнего метода, мы будем использовать библиотеку ABDKMath64x64, которая преобразует результат операций деления в числа с фиксированной точкой.
Опять же, говорят, что использование этой библиотеки повышает точность по сравнению с методом округления до нуля, который доступен по умолчанию в Solidity. Чтобы понять вывод, давайте сравним результаты добавления с функцией div, как показано ниже:
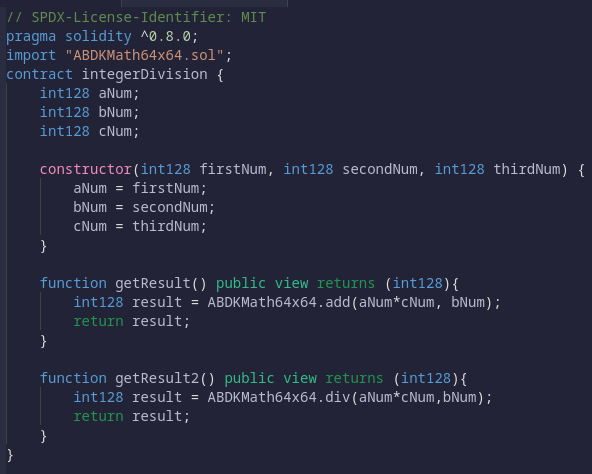
Когда вы добавляете аргументы 1, 1 и 1 при развертывании смарт-контракта, вы получаете значения, как показано ниже:
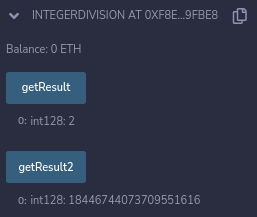
Неудивительно, что функция add возвращает целочисленное значение, равное двум, с тремя аргументами в сумме. Что касается функции div, возвращается значение int 128, представляющее 64,64-битное число с фиксированной запятой со знаком, с которым можно выполнять обычные операции с числами.
Другие библиотеки целочисленного деления, которые стоит рассмотреть
Конечно, библиотека ABDKMath64x64 — не единственная, которую можно использовать для повышения точности, помимо предотвращения ошибки целочисленного деления.
Есть несколько других примеров, например Fixidity, DSMath и библиотеки BANKEX, использующие разные числовые форматы. Форматы чисел, которые отличаются от 64,64-битного числового формата с фиксированной запятой, используемого в приведенном выше примере. Таким образом, хотя эти библиотеки могут показаться полезными для изучения, помните, что их числовые форматы не будут работать ни с какими другими доступными библиотеками.
Оригинал

