Как фокусировка разрешает застрявшие термины в основной оценке
8 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
3.2 Сосредоточение внимания на оценке в сердечнике
Давайте теперь вернемся к проблеме в ядре и найдем решение для застрявшего термина 𝜇𝛼. + (𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽), ⌜5⌝; 𝛼). Мы знаем, что должны оценить 𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽) Далее, а затем как -то подключите промежуточный результат в отверстие [·] в производителе 𝜇𝛼. + ([·], ⌜5⌝; 𝛼). Если мы дадим промежуточный результат название 𝑥 и поиграем с разрезами, 𝜇-связками и привязками, мы можем обнаружить, что мы можем рекомбинировать все эти части следующим образом:
𝜇𝛼.⟨𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽) | 𝜇𝑥. ˜ + (𝑥, ⌜5⌝; 𝛼)⟩
Его термин выглядит немного загадочно, но преобразование примерно соответствует тому, что происходит, когда мы переводим термин «Пусть 𝑥 = 2» 4 в 𝑥 + 5 вместо (2 ∗ 4) + 5 в ядро. То есть мы подняли субкомпутацию на внешнюю часть термина, который мы оцениваем. Этот вид трансформации называется фокусировкой [Andreoli 1992; Curien и Munch-Maccagnoni 2010] и мы используем ее для решения проблемы с застрявшими терминами в ядре. Мы видим, что это сработало в нашем примере, потому что термин теперь полностью оценивается в ее нормальную форму.
Пример3.1. Производитель 𝜇𝛼.⟨𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽) | 𝜇𝑥. ˜ + (𝑥, ⌜5⌝; 𝛼)⟩ уменьшается следующим образом:
⟨𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽) | 𝜇𝑥. ˜ + (𝑥, ⌜5⌝; ⋆)⟩ ⊲ ∗ (⌜2⌝, ⌜4⌝; 𝜇𝑥. ˜ + (𝑥, ⌜5⌝; ⋆))
⊲ ⟨⌜8⌝ | 𝜇𝑥. ˜ + (𝑥, ⌜5⌝; ⋆)⟩
⊲ +(⌜8⌝, ⌜5⌝; ⋆) ⊲ ⟨⌜13⌝ | ⋆⟩
Как только мы убедились в сосредоточенности, у нас есть еще один выбор: хотим ли мы использовать этот трюк во время оценки заявления или в качестве шага предварительной обработки, прежде чем мы начнем с оценки? Эти две альтернативы называются динамической и статической фокусировкой.
Динамическая фокусировкаС динамическим фокусировкой [Wadler 2003] мы добавляем дополнительные правила оценки, обычно называемые 𝜍-rules, для поднятия субкомпьюций на внешнюю часть утверждения, которое мы оцениваем.
Статическое фокусированиеДля статической фокусировки [Curien and Herbelin 2000] мы выполняем преобразование кода, прежде чем начнем его оценивать. Это приводит к целенаправленной нормальной форме, которая является подмножества синтаксисаОсновнойчто мы описали до сих пор.
Динамическая фокусировка отлично подходит для рассуждения о значении программ, но статическая фокусировка более эффективна, если мы заинтересованы в компиляции и заведении программ. По этой причине мы рассматриваем только статическое фокусировку в следующем.

Полные правила статической фокусировки представлены в определении 3.2. Большинство из этих правил связаны только с тем, чтобы выполнить фокусировку преобразования во всех подкрасках, но некоторые из предложений, где происходит что -то интересное, являются положениями для бинарных операторов:
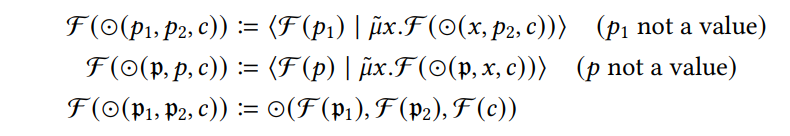
Первые два положения ищут аргументы бинарного оператора ⊙, которые не являются значениями, и используют трюк, описанный выше, чтобы поднять их снаружи. Фокусировка вызывает рекурсивно до тех пор, пока бинарный оператор не применяется только к значениям, и третий пункт не вступит в игру. Этот третий пункт затем применяет фокусирующее преобразование ко всем аргументам бинарного оператора. Положения для конструкторов, деструкторов, IFZ и вызовов к определениям верхнего уровня работают точно так же, как и для бинарных операторов. Следует отметить, что, сосредоточив внимание на аргументах деструкторов, мы гарантируем, что правило оценки для типов кодат может стрелять. Если бы мы не требовали, чтобы аргументы производителя были значениями в этом правиле (но только то, что деструктор является ковалевой), мы могли бы легко ввести сфокусированный термин снова, заменив не значение для переменной.
Трансформация фокусировки, описанная в определении 3.2, не является идеальной, поскольку она создает много административных RedExes. В качестве примера рассмотрим, как сфокусируется утверждение, определяющее Mult ’из примера 2.7:
F (⟨𝑙 | case {nil ⇒ ⟨1 | 𝛽⟩, минусы (𝑥, 𝑥𝑠) ⇒ ifz (𝑥, ⟨0 | 𝛼⟩, ∗ (𝑥, 𝜇𝛾 .mult ’(𝑥𝑠; 𝛼, 𝛾); 𝛽))}⟩)
= ⟨𝑙 | case {nil ⇒ ⟨1 | 𝛽⟩, минусы (𝑥, 𝑥𝑠) ⇒ ifz (𝑥, ⟨0 | 𝛼⟩, ⟨𝜇𝛾 .mult ’(𝑥𝑠; 𝛼, 𝛾) | 𝜇𝑧. ˜ ∗ (𝑥, 𝑧; 𝛽)⟩)}⟩
Фокусировка ввела административный Redex ⟨𝜇𝛾 .mult ’(𝑥𝑠; 𝛼, 𝛾) | 𝜇𝑧. ˜ ∗ (𝑥, 𝑧; 𝛽)⟩ во втором утверждении IFZ. После уменьшения этого Redex до Mult ’(𝑥𝑠; 𝛼, 𝜇𝑧. В реализации мы решаем эту проблему, статически уменьшая административные Redexes на шаге упрощения, но также возможно придумать более сложное определение фокусировки, которое не создает их в первую очередь. Такое оптимизированное фокусирующее преобразование, однако, гораздо менее прозрачна, чем то, что мы описали.
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал

