Насколько централизована децентрализация – работа и методология, связанные с этим

:::информация Этот документ доступен на arxiv по лицензии CC 4.0.

Авторы:

(1) Бартош Кусмир, IOTA Foundation 10405 Берлин, Германия & Кафедра теоретической физики, Вроцлавский университет науки и технологий, Польша bartosz.kusmierz@pwr.edu.pl;

(2) Роман Оверко, Фонд IOTA 10405 Берлин, Германия roman.overko@iota.org.

:::

Таблица ссылок

Аннотация и введение

Связанные работы и методология

Результаты

Краткое содержание и ссылки

II. СВЯЗАННАЯ РАБОТА И МЕТОДОЛОГИЯ

Одна из первых работ, анализирующих Биткойн с использованием характеристик сети с течением времени (а также статистики благосостояния и временных закономерностей транзакций), представлена ​​в [6]. Авторы показали, что богатство крупнейших держателей биткойнов растет быстрее, чем богатство счетов с низким балансом — это явление хорошо известно как преференциальная привязанность, и оно играет существенную роль в формировании распределения богатства. Кроме того, коэффициенты Джини были также рассчитаны для измерения неравенства в богатстве. Анализ сети Биткойн с точки зрения майнинговых пулов можно найти в [20], в которой авторы изучали, как характеристики майнинговых пулов, такие как вычислительная мощность, скорость хеширования, доход от майнинга, стратегии сбора транзакций и размер блока, влияют на безопасность. сети, задержки транзакций и комиссии. Результаты измерений показали, что более 50% блоков были созданы пятью ведущими майнинговыми пулами, что может вызвать проблемы безопасности и централизации сети Биткойн.

Результаты аналогичных нашей работе исследований представлены в [11]. В частности, авторы представили свой анализ с использованием трех различных показателей (коэффициент Джини, энтропия Шеннона и коэффициент Накамото) и их эволюцию с течением времени. Было обнаружено, что степень децентрализации в Биткойне выше и более волатильна, тогда как степень децентрализации в Эфириуме меньше и более стабильна. Дженсен и др. [4] проанализировали децентрализацию распределения токенов управления в четырех приложениях децентрализованного финансирования (DeFi) на блокчейне Ethereum с использованием коэффициентов Джини и Накамото. Их результаты показали, что распределение токенов для всех четырех приложений DeFi характеризуется высокими коэффициентами Джини. Подобные методы использовались в [10], где сравнивались криптовалюты на основе PoW и PoS. Авторы проанализировали децентрализацию Биткойна и Steem, используя энтропию Шеннона. Однако их анализ ограничивался только двумя криптовалютами и не учитывал временные изменения в распределении.

Авторы [22] построили модель роста рыночной капитализации криптовалют, используя закон Гибрата. Они также отметили, что криптомонеты (которые работают в собственной независимой сети DLT) и криптотокены (которые работают поверх другой монетной платформы) следуют закону Ципфа в отношении своей капитализации. Хотя параметр закона Ципфа количественно различен для монет и жетонов.

Большая часть исследований в такой литературе посвящена анализу свойств сетей криптовалют с точки зрения графа, где каждая транзакция представлена ​​ссылкой в ​​графе адресов [2], [9]–[11], [ 15], [16], [19]. Например, Ленберг [9] стремился определить, соответствуют ли отношения между пользователями сетей токенов ERC20 и их оценки закону Меткалфа. Было обнаружено, что только два токена из 50 подчиняются закону Меткалфа, а остальные подчиняются линейному или сублинейному закону.

А. Сбор данных и криптовалютные кошельки

Многие сети блокчейнов не хранят балансы, связанные с адресами; однако балансы могут быть рассчитаны на основе суммы отправленных и полученных активов (т. е. монет или токенов) для каждого адреса. В этой работе мы используем общедоступные наборы данных блокчейна, доступные в Google BigQuery[1]. Начиная с генезис-блока конкретного блокчейна, мы собирали исторические данные о транзакциях/переводах до 16 января 2022 года включительно. В случае некоторых токенов ERC20 первые несколько недель данных были пропущены перед анализом из-за недостаточного количества транзакций. Этот ранний период мог быть посвящен тестированию или маркетингу. Включение этих данных может привести к появлению артефактов[2]

Важно отметить, что данные, представленные в этой статье, отражают не богатство отдельных владельцев криптовалюты, а скорее распределение богатства между криптовалютными кошельками. Криптовалютные кошельки не уникальны для пользователя, и один пользователь может иметь несколько таких кошельков. Истинную личность владельцев адресов установить сложно, и это может быть проблематично даже для организаций, имеющих доступ к данным криптовалютных бирж. Зная об этих ограничениях, мы считаем, что распределение богатства в самых богатых криптовалютных кошельках по-прежнему интересно, поскольку основой систем идентификации в системах PoS и DAO являются кошельки (см. раздел II-B).

Б. Размер выборки N

В этой статье мы анализируем свойства эмпирической функции распределения для N самых богатых счетов. Такие эмпирические распределения являются дискретными, а значение i-й записи представляет собой отношение баланса i-го самого богатого счета к сумме N остатков на самых богатых счетах. Мы ориентируемся на относительно небольшой размер выборки N (30–100). Эти цифры могут показаться произвольными и небольшими, особенно перед лицом тысяч и десятков тысяч пользователей криптовалюты. Однако этот интервал интересен для приложений в DPoS DLT, основанных на механизмах консенсуса Byzantine Fault Tolerance (BFT) [1], [12], [17].

В наиболее стандартных версиях механизмов консенсуса BFT количество участников консенсуса фиксировано, а их личности известны. Такие системы разрешены и не подходят для прямого использования в полностью закрытых ТРР. Однако в ряде блокчейнов DPoS используется интересная модификация конструкции BFT. Эти проекты используют промежуточный этап между открытыми и закрытыми сетями. Любому пользователю разрешено создать узел и собирать токены, но только самые надежные узлы с наибольшей долей напрямую способствуют консенсусу. Иллюстрация процедуры достижения консенсуса на основе закрытого комитета фиксированного размера в открытых и закрытых системах изображена на рис. 1.

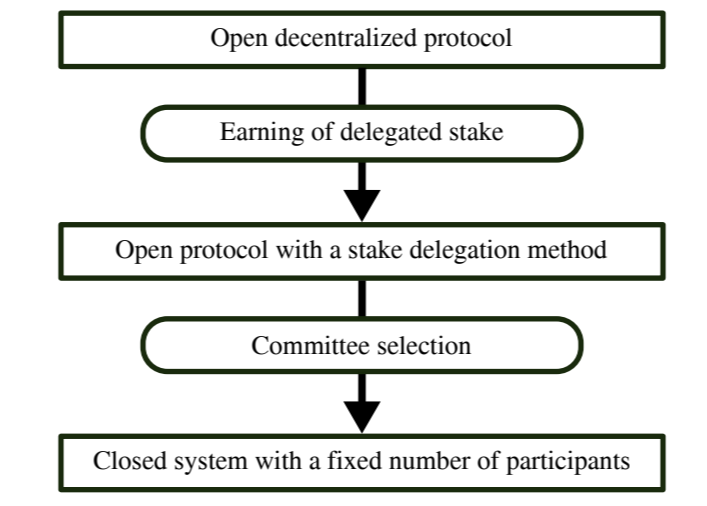
Примером протокола DPoS является EOS[3], в котором блоки создаются комитетом из 21 валидатора, которые коллективно подписывают новые блоки, используя асинхронную версию механизма консенсуса BFT [8]. Члены комитета выбираются и периодически меняются в зависимости от суммы доли, делегированной им другими пользователями сети. Другие примеры включают Lisk[4] , который использует 101 узел, и Интернет-компьютер (ICP)[5] со 101 узлом в нейронной нервной системе (основной блокчейн ICP). Теоретически размер комитета по производству блоков может быть неограниченным. Однако на практике процедура подписания новых блоков ограничена пропускной способностью — количество сообщений, которыми обмениваются члены комитета, растет пропорционально квадрату его размера. В большинстве практических случаев комитет по производству блоков состоит из от 10 до 50 членов. Некоторые из протоколов мультиблокчейна могут позволить себе использовать до 100 узлов в некоторых частях своего протокола; однако в этих случаях страдает время изготовления блока. Эти ограничения объясняют наш интерес к относительно небольшому интервалу размера выборки N, а именно 30–100, который можно использовать для моделирования распределения токенов среди валидаторов блоков или улучшения процесса отбора комитетов.

С. Закон Ципфа

Распределение Ципфа — это дискретное распределение, обычно встречающееся в физике и социальных науках. Эмпирически подтверждено, что закон Ципфа описывает множество эффектов в количественной лингвистике [23], изучении населения страны и города [3], ссылок на веб-сайты и других эффектов. Возможно, наиболее актуальными для этой статьи являются применения закона Ципфа при моделировании благосостояния общества [5] и распределение держателей токенов в различных криптовалютах [6], [7], [10].

Д. Показатели централизации

В этой статье мы обсуждаем множественные метрики централизации, такие как Джини и коэффициент Накамото. Мы хотим еще раз подчеркнуть, что размер анализируемой выборки N относительно невелик и может существенно влиять на значения этих показателей из-за коэффициента нормализации H(s, N) в уравнении. (1).

В общем случае значения энтропии неограниченны. Однако когда количество доступных состояний N фиксировано, энтропия принимает значения из интервала [0, log(N)]. Максимальная централизация соответствует энтропии, равной нулю, а децентрализация растет с ростом энтропии.

2) Коэффициент Джини. Коэффициент Джини G — это показатель неравенства, широко используемый в экономике и социальной статистике:

это минимальное количество участников, контролирующих более половины сетевых ресурсов. Первоначально он был введен для оценки возможности атаки 51% на сеть Биткойн.

[1] https://bigquery.cloud.google.com/dataset/bigquery-public-data

[2] Например, в течение первых нескольких недель после создания смарт-контракта Tether (USDT) передачи токенов не было.

[3] https://eos.io/

[4] https://lisk.com/

[5] https://dfinity.org/