Hinge Loss — функция оценки устойчивых потерь для моделей классификации SVM в AI и ML

5 января 2023 г.

Машинное обучение — это не что иное, как проблема оптимизации. Исследователи используют алгебраический акме под названием «Потери», чтобы оптимизировать пространство машинного обучения, определяемое конкретным вариантом использования. «Потери» можно рассматривать как расстояние между истинными значениями проблемы и значениями, предсказанными моделью. Чем больше потери, тем больше ошибок вы допустили в данных. Большинство показателей оценки производительности, таких как точность, достоверность, отзыв, оценка f1 и т. д., являются косвенным производным от функций потерь. Исследователи реализовали множество функций потерь, например:

* Для задач регрессии — среднеквадратическая ошибка, среднее значение абсолютной ошибки, потеря Хьюбера, логарифмическая потеря, квантильная потеря и т. д. * Для задач бинарной классификации — потери двоичной перекрестной энтропии, потери шарнира и т. д. * Для задачи множественной классификации – многоклассовая перекрестная потеря энтропии, KL-дивергенция

В этой статье я познакомлю вас со сложной метрикой потерь под названием «Потери шарнира», которая обсуждается в некоторых из наиболее рекомендуемых учебников по прогнозному моделированию. Я надеюсь, что объяснение будет понятным как визуально, так и математически, чтобы помочь начинающим энтузиастам в области машинного обучения.

Концепция потери петли

Потери шарнира — это функция, широко используемая в алгоритмах метода опорных векторов для измерения расстояния точек данных от границы решения. Это помогает приблизить вероятность неправильных прогнозов и оценить производительность модели.

Некоторые из других широко используемых функций потерь в алгоритмах классификации:

• Примеси Джини
• Логарифмическая потеря
• Ошибка неправильной классификации и т. д.

Метод опорных векторов – это контролируемый алгоритм машинного обучения, который широко используется для прогнозирования категории помеченных точек данных.

Например-

• Предсказание того, мужчина это или женщина.
• Предсказание, является ли фрукт яблоком или апельсином.
• Прогнозирование того, сдаст или не сдаст студент экзамены и т. д.

SVM использует воображаемую плоскость, которая может перемещаться по нескольким измерениям для целей прогнозирования. Эти воображаемые плоскости, которые могут перемещаться в нескольких измерениях, называются гиперплоскостями. Очень сложно представить более высокие измерения с помощью человеческого мозга, поскольку наш мозг естественным образом способен визуализировать только до трех измерений.

Давайте рассмотрим простой пример, чтобы понять этот сценарий.

У нас есть задача классификации, чтобы предсказать, сдаст или не сдаст студент экзамен. У нас есть следующие функции в качестве независимых переменных-

• Отметки на внутренних экзаменах
• Отметки в проектах
• Процент посещаемости

Итак, эти 3 независимые переменные становятся 3-мя измерениями такого пространства-

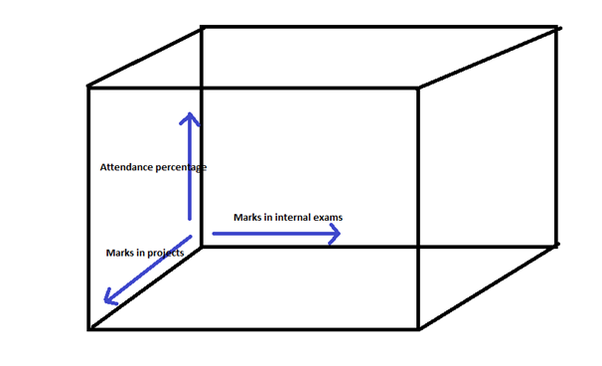
Предположим, что наши точки данных выглядят так, где-

• Зеленым цветом отмечены учащиеся, сдавшие экзамен.
• Красным цветом отмечены учащиеся, не сдавшие экзамен.

Теперь SVM создаст гиперплоскость, которая проходит через эти 3 измерения, чтобы различать неудачников и сдавших экзамен

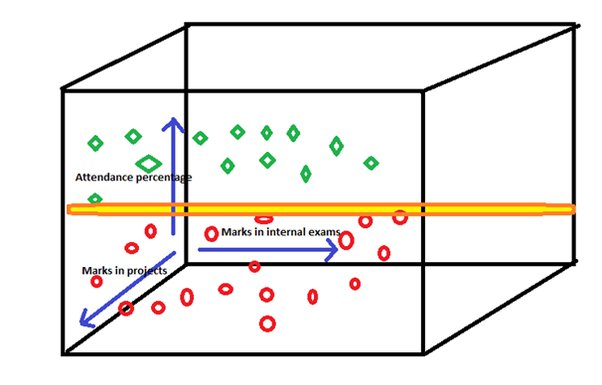
Итак, технически теперь модель понимает, что все точки данных, попадающие на одну сторону гиперплоскости, принадлежат сдавшим экзамены студентам, и наоборот. Эта гиперплоскость называется границей решения или гиперплоскостью максимального запаса. Расстояние от точки данных до границы решения показывает надежность прогноза.

На следующем изображении показана лучшая визуализация-

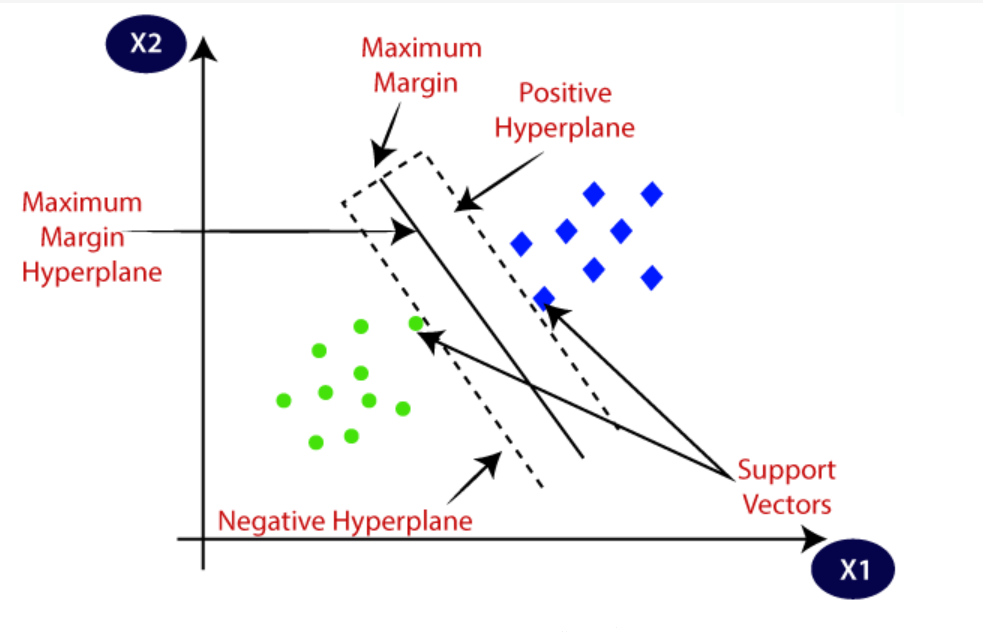
Логично,

• Если расстояние между границей решения и точкой данных относительно велико, это означает, что модель в некоторой степени уверена в своем прогнозе.
• Если расстояние между границей решения и точкой данных относительно невелико, это означает, что модель менее уверена в своем прогнозе.

Следующее изображение даст вам лучшее представление -

n Здесь

Значение границы решения равно нулю.

• "+" указывает на предсказание положительного класса.
• "-" Указывает на предсказание отрицательного класса.
• yf(x) – функция потерь шарнира.

Есть 2 основных сценария, в которых исследователи используют потерю шарнира в SVM-

Сценарий 1 (данные для обучения): оптимальное построение модели в многомерном пространстве, что снижает вероятность ошибочной классификации и расширяет возможности принятия решений.

Это также помогает построить наиболее подходящую границу решения, выбирая ту границу решения, которая имеет минимальную потерю шарнира из множества вариантов с помощью метода проб и ошибок или настройки гиперпараметров (этот подход аналогичен процессу поиска наилучшего соответствует линии линейной регрессии в процессе обучения).

Сценарий 2 (при тестировании данных): для оценки производительности модели SVM.

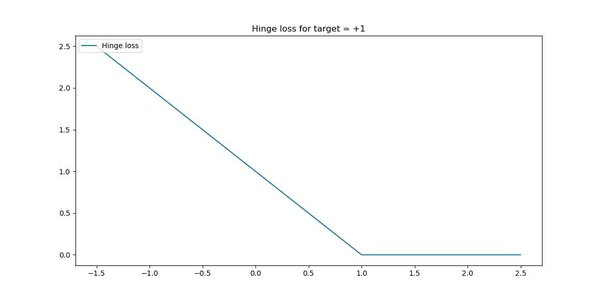
Давайте разберемся с расчетом потери шарнира в SVM по отношению к сценарию 1. На изображении ниже показано визуальное представление функции потери шарнира.

* По оси X показано расстояние от границы решения до точки данных. * По оси Y показан размер потерь или штраф, который вычисляет функция потерь шарнира для определенной точки данных.

Пунктирная линия представляет число 1 на оси X. Если модель правильно предсказывает точку данных и ее расстояние от границы решения больше 1, то потери минимальны (почти нулевые).

Если точка данных находится точно на границе решения, то потеря шарнира будет иметь значение 1 (очевидно, что расстояние между границей решения и точкой данных будет равно нулю).

Если точка данных неверно предсказана (классифицирована) моделью, есть 2 возможности:

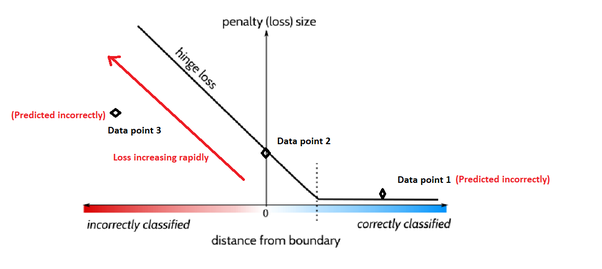
Возможность 1. Расстояние между точкой данных и границей решения находится в положительном направлении (точка данных 1 на изображении выше).

Возможность 2. Расстояние между точкой данных и границей решения находится в отрицательном направлении (точка данных 3 на изображении выше).

В варианте 1 потеря шарнира не будет быстро увеличиваться, т. е. значение потери будет ниже.

Например,

Предположим, что значение границы решения равно 0, а значение прогнозируемой точки данных равно +2,5 (но фактическое значение должно быть ниже 0, поскольку это неверный прогноз). Здесь разница между прогнозируемым значением и границей решения составляет +2,5. Следовательно, потери на петлях будут низкими (это обозначено точкой данных 1 на изображении выше).

В варианте 2 потери шарнира будут быстро увеличиваться, т. е. значение потерь будет высоким.

Например,

Предположим, что значение границы решения равно 0, а значение прогнозируемой точки данных равно -1,5 (но фактическое значение должно быть выше 0, поскольку это неверный прогноз). Здесь разница между прогнозируемым значением и границей решения составляет -1,5. Следовательно, потери шарнира будут высокими (это показано как точка данных 3 на изображении выше).

Давайте посчитаем потери шарнира для этих двух возможностей-

Как мы обсуждали ранее,

• Значение потери шарнира равно 1, когда значение прогнозируемой точки данных равно 0.
• Согласно варианту 1, если значение прогнозируемой точки данных равно +2,5, то потери шарнира этого прогноза равны нулю.
• Согласно варианту 2, если значение прогнозируемой точки данных равно -1,5, то потеря шарнира этого прогноза составляет 2,5.

Аналогично для модели можно рассчитать потери шарнира для каждой точки данных. Когда модель SVM строится в многомерной плоскости, мы всегда должны стараться максимально минимизировать потери шарнира, чтобы повысить прогностическую способность модели.

Пример в реальном времени с образцом набора данных

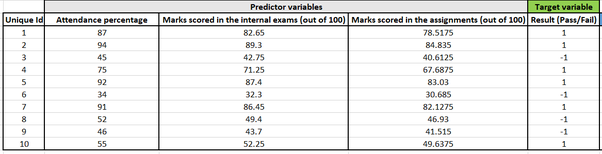
Представьте, что у нас есть задача бинарной классификации, чтобы предсказать, сдаст или не сдаст экзамен учащийся на основе следующих переменных-предикторов:

* Процент посещаемости * Баллы на внутренних экзаменах * Баллы за задания

Мы обучили нашу модель с 1000 записями, и теперь у нас есть следующая таблица в качестве тестовых данных:

н

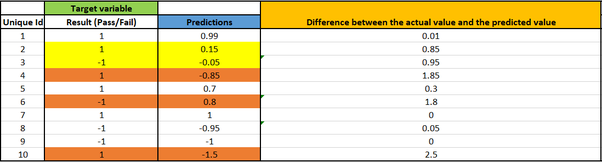
Мы оцениваем модель, используя следующие тестовые данные, и делаем прогнозы. Наши прогнозы таковы:

Прогнозируемое значение будет числом от -1 до 1 с погрешностью 0,2. Если значение меньше или равно нулю, то прогнозируемый класс будет считаться -1, а если значение больше нуля, то прогнозируемый класс будет считаться +1.

Поскольку маржа равна 0,2, а граница решения равна 0. Потери шарнира рассчитываются для –

• Все неверные прогнозы
• Все верные прогнозы в диапазоне [-0,2, +0,2]

Потери шарнира следующие:

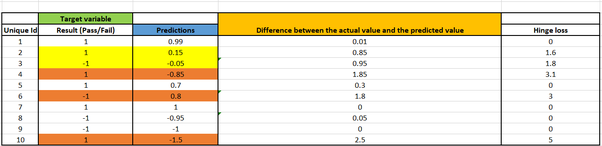
* Точки данных с уникальным идентификатором 1, 5, 7, 8 и 9 прогнозируются правильно. Следовательно, для этих случаев нет потерь шарнира. * Точки данных с уникальными идентификаторами 4, 6 и 10 прогнозируются неправильно. Следовательно, потери шарнира рассчитываются для этих точек данных. * Точки данных с уникальными идентификаторами 2 и 3 прогнозируются правильно, но их значение находится в допустимом диапазоне. Следовательно, потери шарнира рассчитываются для этих точек данных. * Полная потеря шарнира модели представляет собой среднее значение всех этих значений = (1,6 + 1,8 + 3,1 + 3 + 5) / 10 = 1,45

Ссылки

• Потеря шарнира — Википедия
• Росаско, Л.; Де Вито, Э.Д.; Капонетто, А .; Пиана, М.; Верри, А. (2004). "Все ли функции потерь одинаковы?" (PDF)? Нейронные вычисления. 16 (5): 1063–1076. CiteSeerX 10.1.1.109.6786. doi:10.1162/089976604773135104. PMID 15070510.
• Дуан, К.Б.; Кирти, СС (2005). "Какой мультиклассовый метод SVM является лучшим? Эмпирическое исследование" (PDF). Несколько систем классификации. LNCS. Том. 3541. стр. 278–285. CiteSeerX 10.1.1.110.6789. doi:10.1007/11494683_28. ISBN 978-3-540-26306-7.
• Ренни, Джейсон Д. М.; Сребро, Натан (2005). Функции потерь для уровней предпочтения: регрессия с дискретными упорядоченными метками (PDF). проц. IJCAI Междисциплинарный семинар по достижениям в обработке предпочтений.

---

Оригинал