Искаженные схемы: базовая схема и приложения

Особая благодарность Данкраду Файсту за отзыв

[Искаженные схемы] (https://en.wikipedia.org/wiki/Garbled_circuit) — довольно старый и удивительно простой криптографический примитив; вполне возможно, что они представляют собой простейшую форму универсальных «многосторонних вычислений» (MPC).

Вот обычная настройка для схемы:

• Предположим, что есть две стороны, Алиса и Боб, которые хотят вычислить некоторую функцию f(alice_inputs, bob_inputs), которая принимает входные данные от обеих сторон. Алиса и Боб оба хотят узнать результат вычисления f, но Алиса не хочет, чтобы Боб узнал ее входные данные, а Боб не хочет, чтобы Алиса узнала его входные данные. В идеале они оба ничего не узнают, кроме вывода f.

• Алиса выполняет специальную процедуру («искажение») для шифрования схемы (имеется в виду набор логических элементов И, ИЛИ...), которая оценивает функцию f. Она передает входные данные, также зашифрованные способом, совместимым с зашифрованной схемой, Бобу.

• Боб использует технику, называемую «забывчивая передача 1 из 2», чтобы узнать зашифрованную форму своих собственных входных данных, не сообщая Алисе, какие входные данные он получил.

• Боб запускает зашифрованную схему на зашифрованных данных, получает ответ и передает его Алисе.

Дополнительные криптографические оболочки могут использоваться для защиты схемы от Алисы и Боба, отправляющих неверную информацию и дающих друг другу неправильный ответ; мы не будем вдаваться в них для простоты, хотя достаточно сказать, что «обернуть ZK-SNARK вокруг всего» — это одно (довольно тяжелое и неоптимальное!) решение, которое отлично работает.

Так как же работает базовая схема? Начнем со схемы:

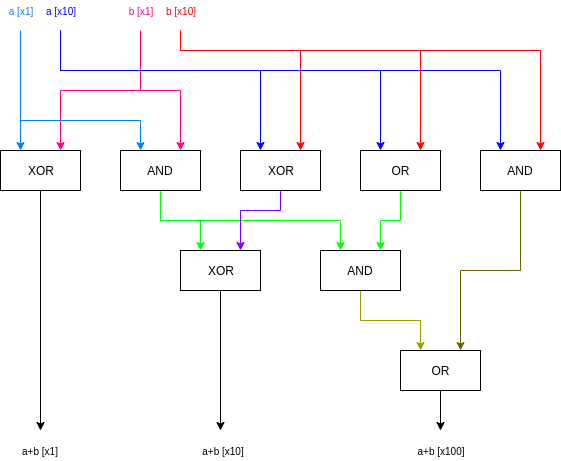
Это один из простейших примеров не совсем тривиальной схемы, которая действительно что-то делает: это двухбитный сумматор. Он принимает на вход два двоичных числа, каждое из которых состоит из двух битов, и выводит трехбитное двоичное число, представляющее собой сумму.

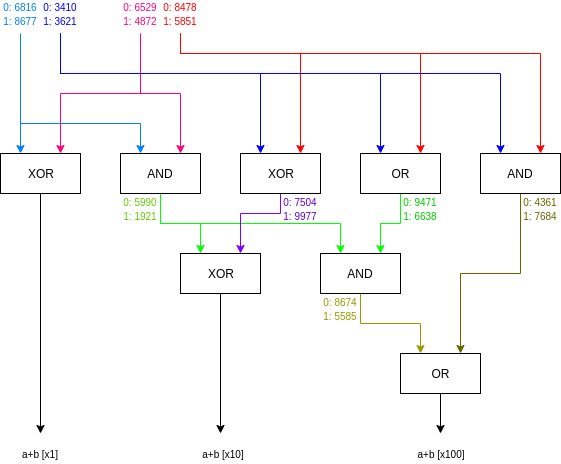
Теперь давайте зашифруем цепь. Во-первых, для каждого входа мы случайным образом генерируем две «метки» (например, 256-битные числа): одну для представления этого входа как 0, а другую для представления этого входа как 1. Затем мы также делаем то же самое для каждого промежуточного провода, не включая выходные провода. Обратите внимание, что эти данные не являются частью «искажений», которые Алиса посылает Бобу; пока это только настройка.

Теперь для каждого вентиля в схеме делаем следующее. Для каждой комбинации входных данных мы включаем в «искажение», которое Алиса предоставляет Бобу, метку вывода (или, если метка вывода является «конечным» выводом, непосредственно вывод), зашифрованную с помощью ключа, сгенерированного путем хэширования входные метки, которые ведут к этому выходу вместе. Для простоты наш алгоритм шифрования может быть просто «enc(out, in1, in2) = out + hash(k, in1, in2)», где «k» — это индекс логического элемента (это первый вентиль в цепи, второй, третий?). Если вы знаете метки обоих входов и у вас есть искажения, то вы можете узнать метку соответствующего вывода, потому что вы можете просто вычислить соответствующий хэш и вычесть его.

Вот искажение первого вентиля XOR:

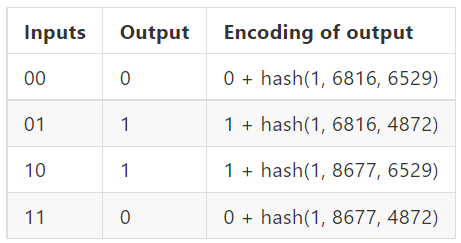Обратите внимание, что мы включаем (зашифрованные формы) 0 и 1 напрямую, потому что выходные данные этого элемента XOR являются прямыми окончательными выходными данными программы. . Теперь давайте посмотрим на крайний левый логический элемент И:

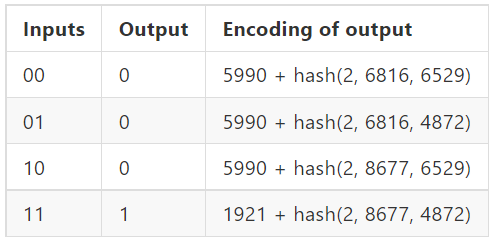Здесь выходы вентиля просто используются как входы для других вентилей, поэтому мы используем метки вместо битов, чтобы скрыть эти промежуточные биты от оценщик.

«Искажение», которое Алиса предоставила бы Бобу, — это просто все в третьем столбце для каждого вентиля, с переупорядоченными строками каждого вентиля (чтобы избежать выявления того, соответствует ли данная строка 0 или 1 в любом проводе). Чтобы помочь Бобу узнать, какое значение расшифровывать для каждого вентиля, мы будем использовать определенный порядок: для каждого вентиля первая строка становится строкой, в которой обе входные метки четные, во второй строке вторая метка нечетная, в третьей строке первая метка нечетная, а в четвертой строке обе метки нечетные (мы намеренно выбрали метки раньше, чтобы у каждого элемента была четная метка для одного выхода и нечетная для другого). Таким же образом мы искажаем все остальные ворота в схеме.

Всего Алиса посылает Бобу четыре \~256-битных числа для каждого вентиля в схеме. Оказывается, четыре — это далеко не оптимально; см. [здесь] (http://web.mit.edu/sonka89/www/papers/2017ygc.pdf) для некоторых оптимизаций того, как уменьшить это до трех или даже двух чисел для вентиля И и нуля (!!) для ворота XOR. Обратите внимание, что эти оптимизации основаны на некоторых изменениях, например. используя XOR вместо сложения и вычитания, хотя это все равно следует делать в целях безопасности.

Когда Боб получает схему, он запрашивает у Алисы метки, соответствующие ее вводу, и использует протокол, называемый «забывчивой передачей 1 из 2», чтобы запросить у Алисы метки, соответствующие его собственному вводу, не раскрывая Алисе, что его ввод является. Затем он проходит через вентили в цепи один за другим, обнажая выходные провода каждого промежуточного вентиля.

Предположим, что вход Алисы — это два левых провода, и она дает (0, 1), а ввод Боба — это два правых провода, и он дает (1, 1). Вот снова схема с метками:

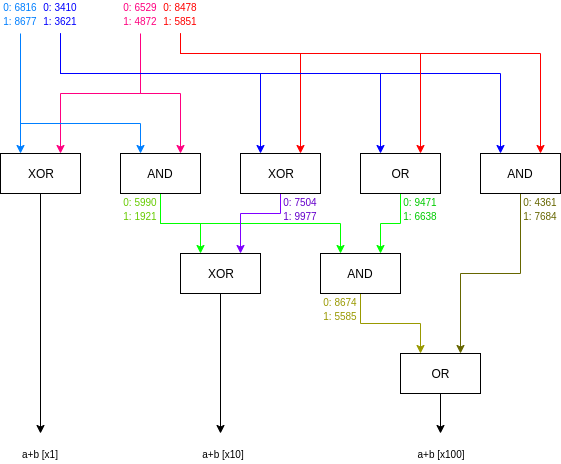
• В начале Боб знает метки 6816, 3621, 4872, 5851

• Боб оценивает первые ворота. Он знает 6816 и 4872, поэтому он может извлечь выходное значение, соответствующее (1, 6816, 4872) (см. таблицу выше), и извлекает первый выходной бит, 1

• Боб оценивает вторые ворота. Он знает 6816 и 4872, поэтому он может извлечь выходное значение, соответствующее (2, 6816, 4872) (см. таблицу выше), и извлекает метку 5990.

• Боб оценивает третий вентиль (XOR). Он знает 3621 и 5851, а выучивает 7504.

• Боб оценивает четвертые ворота (ИЛИ). Он знает 3621 и 5851, а выучил 6638.

• Боб оценивает пятые ворота (И). Он знает 3621 и 5851, а выучивает 7684.

• Боб оценивает шестой вентиль (исключающее ИЛИ). Он знает 5990 и 7504 и узнает второй выходной бит, 0.

• Боб оценивает седьмые ворота (И). Он знает 5990 и 6638, а выучил 8674.

• Боб оценивает восьмые ворота (ИЛИ). Он знает 8674 и 7684 и выучивает третий выходной бит, 1.

Итак, Боб узнает вывод: 101. И в двоичном виде 10 + 11 фактически равно 101 (входные и выходные биты даны в порядке от наименьшего к наибольшему в схеме, поэтому вход Алисы 10 представлен как (0, 1) в схеме), так и заработало!

1 из 2 Забывчивая передача

Теперь давайте поговорим подробнее об забывчивом переносе 1 из 2 — методе, который Боб использовал для получения от Алисы меток, соответствующих его собственному вводу. Проблема вот в чем. Сосредоточившись на первом входном бите Боба (алгоритм для второго входного бита такой же), Алиса имеет метку, соответствующую 0 (6529), и метку, соответствующую 1 (4872). У Боба есть желаемый входной бит: 1. Боб хочет узнать правильную метку (4872), не давая Алисе знать, что его входной бит равен 1. Тривиальное решение (Алиса просто посылает Бобу и 6529, и 4872) не работает, потому что только Алиса хочет отказаться от одной из двух входных меток; если Боб получит обе входные метки, это может привести к утечке данных, от которых Алиса не хочет отказываться.

Вот [довольно простой протокол] (https://crypto.stanford.edu/pbc/notes/crypto/ot.html) с использованием эллиптических кривых:

1. Алиса создает случайную точку эллиптической кривой «H».

1. Боб генерирует две точки, «P1» и «P2», с условием, что сумма «P1 + P2» равна «H». Боб выбирает P1 или P2 как G * k (т. е. точку, для которой он знает соответствующий закрытый ключ). Обратите внимание, что требование, что P1 + P2 = H, гарантирует, что Боб не сможет сгенерировать P1 и P2, для которых он знает соответствующий закрытый ключ. Это потому, что если "P1 = G * k1" и "P2 = G * k2", где Боб знает и "k1", и "k2", то "H = G * (k1 + k2)", а это означает, что Боб может извлеките дискретный логарифм (или «соответствующий закрытый ключ») для H, что будет означать, что вся криптография на эллиптических кривых взломана.

1. Алиса подтверждает «P1 + P2 = H» и шифрует «v1» под «P1» и «v2» под «P2», используя некоторую стандартную схему шифрования с открытым ключом (например, [Эль-Гамаль] (https://en .wikipedia.org/wiki/ElGamal_encryption)). Боб может расшифровать только одно из двух значений, потому что он знает закрытый ключ, соответствующий не более чем одному из (P1, P2), а Алиса не знает, какому из них.

Это решает проблему; Боб узнает одну из двух меток проводов (либо 6529, либо 4872), в зависимости от того, какой у него входной бит, и Алиса не знает, какую метку выучил Боб.

Приложения

Искаженные схемы потенциально полезны для гораздо большего, чем просто вычисление 2 из 2. Например, вы можете использовать их для многосторонних вычислений произвольной сложности с произвольным количеством участников, предоставляющих входные данные, которые могут выполняться в постоянном количестве раундов взаимодействия. Генерация искаженной схемы полностью распараллеливается; вам не нужно заканчивать искажать одни ворота, прежде чем вы сможете начать искажать ворота, которые от них зависят. Следовательно, вы можете просто провести большое многостороннее вычисление, в котором многие участники вычисляют искажение всех элементов схемы и публикуют метки, соответствующие их входам. Сами метки являются случайными и поэтому ничего не говорят о входных данных, но затем любой может выполнить опубликованную искаженную схему и узнать вывод «в открытом виде». См. [здесь] (https://eprint.iacr.org/2017/189.pdf) недавний пример протокола MPC, который использует искажение в качестве ингредиента.

Многосторонние вычисления — не единственный контекст, в котором полезен этот метод разделения вычислений на параллелизуемую часть, которая работает с секретными данными, за которой следует последовательная часть, которая может выполняться в открытом виде, и искаженные схемы — не единственный метод для выполнение этого. В целом литература по [рандомизированным кодировкам] (https://eprint.iacr.org/2017/385.pdf) включает множество более сложных методов. Эта ветвь математики также полезна в таких технологиях, как функциональное шифрование и обфускация.

Эта статья изначально была опубликована как «[Краткое руководство по искаженным схемам] (https://vitalik.ca/general/2020/03/21/garbled.html)».