ПОТОК ПАРА ЧЕРЕЗ ТРУБЫ И ОТВЕРСТИЯ

Steam, его создание и использование от Babcock & Компания Wilcox входит в серию книг HackerNoon. Вы можете перейти к любой главе этой книги здесь. ПОТОК ПАРА ЧЕРЕЗ ТРУБЫ И ОТВЕРСТИЯ

ПОТОК ПАРА ЧЕРЕЗ ТРУБЫ И ОТВЕРСТИЯ

Были выдвинуты различные формулы для потока пара по трубам, все они основаны на теореме Бернулли о потоке воды по круглым трубам с соответствующими модификациями, внесенными для изменения констант между паром и водой. Потери энергии из-за трения в трубе определяются Анвином (на основе Вейсбаха) как

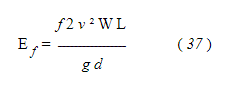
где E — потеря энергии в футо-фунтах из-за трения W единиц веса пара, проходящего со скоростью v футов в секунду через трубу диаметром d футов и длиной L футов; g представляет ускорение свободного падения (32.2), а f - коэффициент трения.

Были даны многочисленные значения коэффициента трения f , который, как показывает эксперимент, очевидно, зависит как от диаметра трубы, так и от скорости проходящего пара. Достоверных данных о скорости этого изменения скорости нет, и, как и во всех экспериментах, эффект изменения скорости оказался меньшим, чем неизбежные ошибки наблюдения; предполагается, что коэффициент изменяется только в зависимости от размера трубы.

Анвин установил зависимость для этого коэффициента для пара со скоростью 100 футов в секунду

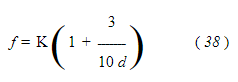
где K — константа, определенная экспериментально, а d — внутренний диаметр трубы в футах.

Если h представляет собой потерю головы в ногах, то

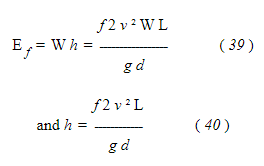
Если D представляет собой плотность пара или вес на кубический фут, а p — потерю давления из-за трения в фунтах на квадратный дюйм, то

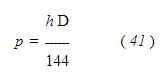
и из уравнений (38), (40) и (41),

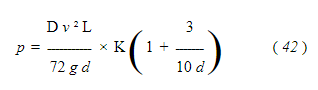
Чтобы преобразовать термин скорости и привести его к обычно используемым единицам измерения, пусть d 1 — диаметр трубы в дюймах = 12 d, а w — расход в фунтах в минуту; тогда

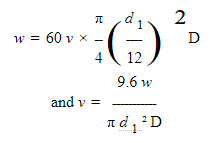
Подставив это значение и значение d в формулу ( 42 )

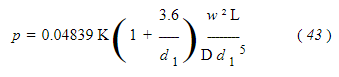
Некоторые экспериментальные определения значения K:

К = 0,005 для воды (Унвин). K = 0,005 для воздуха (поджог). K = 0,0028 для воздуха (эксперименты в туннеле Сен-Готард). K = 0,0026 для пара (Плотник из Орискани). K = 0,0027 для пара (Г. Х. Бэбкок).

Значение 0,0027, по-видимому, является наиболее правильным, и подстановка в формулу (43) дает:

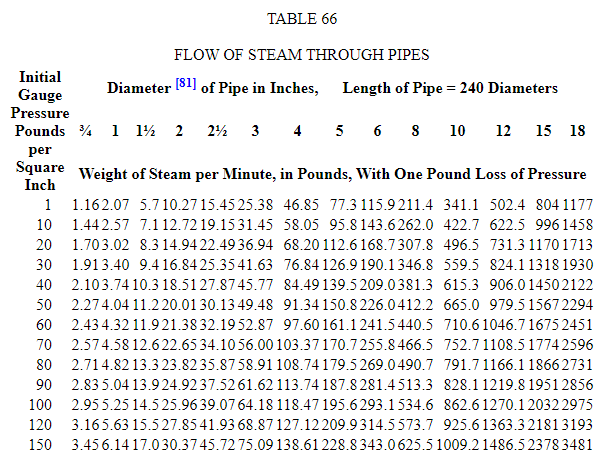
Эта формула является наиболее общепринятой для течения пара в трубах. Таблица 66 рассчитана по этой формуле и дает количество пара, проходящего в минуту. который будет течь по прямым гладким трубам длиной 240 диаметров при различных начальных давлениях с разницей в один фунт между начальным и конечным давлениями.

Чтобы применить эту таблицу для других длин труб и потерь давления, отличных от предполагаемых , пусть L = длина и d диаметр трубы, оба в дюймах; l — потеря в фунтах; Q — вес в условиях, принятых в таблице, и Q 1, вес измененных условий.

Для любой длины трубы, если вес проходящего пара такой же, как указан в таблице , потеря составит,

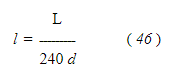
Если длина канала такая же, как предполагалось в таблице, но потери другое, то количество пара, проходящего в минуту, будет,

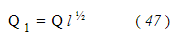
При любой предполагаемой длине трубы и потере давления вес будет равен

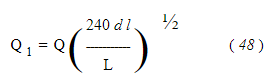
Чтобы получить падение давления для длин, отличных от 1000 футов, умножьте на длину в футах ÷ 1000.

Пример: Найдите вес пара при первоначальном манометрическом давлении 100 фунтов, который пройдет через 6-дюймовую трубу длиной 720 футов с перепадом давления 4 фунта. В условиях, предполагаемых в таблице, в минуту будет течь 293,1 фунта; следовательно, Q = 293,1 и

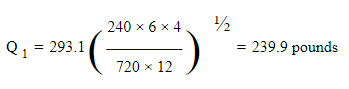
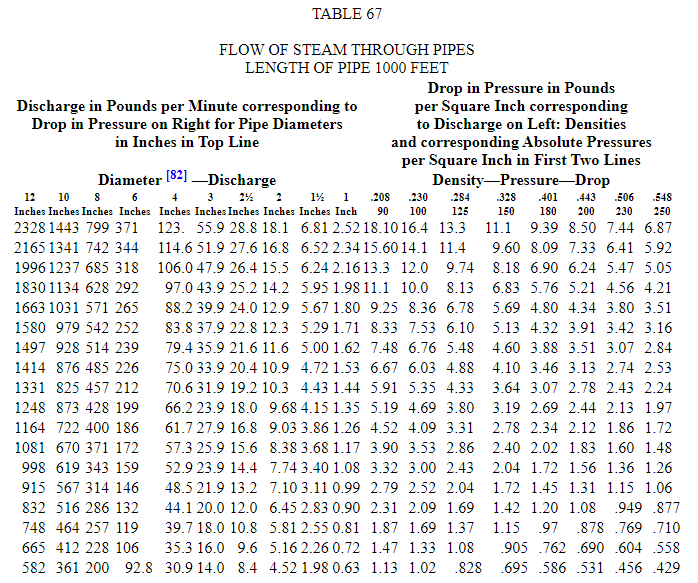
Таблица 67 часто оказывается полезной при решении проблем, связанных с потоком пар. Эта таблица была рассчитана г-ном Э. К. Сиклзом для трубы длиной 1000 футов от формула ( 45 ), за исключением того, что из при использовании значения константы K = 0,0026 вместо 0,0027 константа в формуле становится 87,45 вместо 87.

При использовании этой таблицы необходимо учитывать давления и плотности, как указано в верхняя часть правой части представляет собой среднее значение начального и конечного давления и плотности. Его использование заключается в следующем: предположим допустимое падение давления на трубе заданной длины. От значения, найденного в правом столбце под столбцом среднего давления, определенного начальным и конечным давлением, перейдите к левой части таблицу по той же строке, пока не будет найдено количество, соответствующее требуемому потоку. Размер трубы в головной части этой колонны такой, чтобы переносить необходимое количество пара при предполагаемом перепаде давления.

Таблицу можно использовать и наоборот, для определения падения давления в трубе заданного диаметра, поставляющего определенное количество пара путем перехода от известной цифры слева к колонне справа, возглавляемой давлением, которое является средним значением начального и конечного давлений, соответствующих найденному перепаду и фактическому присутствующему начальному давлению.< /п>

Для заданного расхода пара и диаметра трубы падение давления пропорционально длине, и если требуются объемы сброса для труб другой длины, кроме 1000 футов, их можно найти пропорционально.

Колено, запорные клапаны и вход в трубы с квадратным концом обеспечивают сопротивление прохождению пара. Сопротивление такой конструкции принято измерять диаметром трубы. Было разработано множество формул для расчета длины трубы диаметром, эквивалентным фитингам или клапанам, оказывающим сопротивление. Однако эти формулы сильно различаются, и для обычных целей они будут достаточно точными, чтобы учесть сопротивление на входе трубы длиной, равной 60-кратному диаметру; для прямоугольного колена длина равна 40 диаметрам, а для проходного клапана длина равна 60 диаметрам.

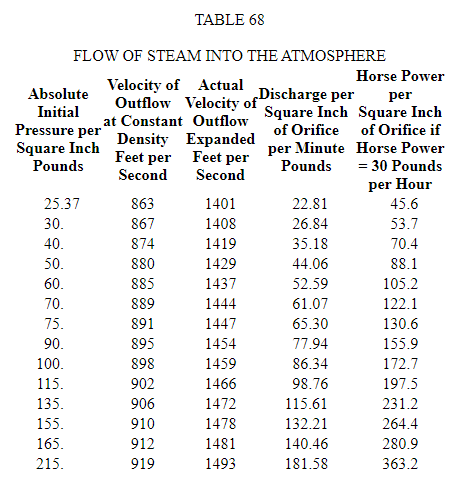
Поток пара от более высокого давления к более низкому увеличивается по мере того, как разница давлений увеличивается до точки, где внешнее давление становится 58 процентов от абсолютного начального давления. Ниже этой точки поток не увеличивается и не уменьшается из-за уменьшения внешнего давления, даже до достижения идеального вакуума. Самое низкое давление, для которого справедливо это утверждение, когда пар выбрасывается в атмосферу, составляет 25,37 фунтов. При любом давлении ниже этой цифры атмосферное давление, равное 14,7 фунтам, превышает 58 процентов первоначального давления. Таблица 68, составленная Д.К. Кларком, показывает скорость оттока при постоянной плотности: фактическая скорость истечения увеличилась (атмосферное давление принято равным 14,7 фунтам абсолютного давления, а коэффициент расширения в сопле равен 1,624), и соответствующий расход на квадратный дюйм отверстия в минуту.

Непер вывел приблизительную формулу истечения пара в атмосферу, которая близко соответствует только что приведенным цифрам. Эта формула:

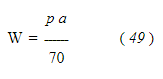
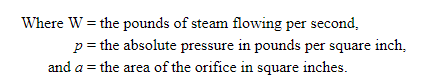
В некоторых опытах профессора Ч. Х. Пибоди при течении пара по трубам длиной от ¼ дюйма до 1½ дюйма и диаметром ¼ дюйма с закругленными входами наибольшее отличие от формулы Нейпира составило 3,2% превышения экспериментального значения над расчетным. результаты.

Для пара, проходящего через отверстие от более высокого давления к более низкому, где более низкое давление превышает 58 процентов от более высокого, расход в минуту можно рассчитать по формуле:

О книжной серии HackerNoon: мы предлагаем вам наиболее важные технические, научные и познавательные книги, являющиеся общественным достоянием.

Эта книга является общественным достоянием. Бэбкок и amp; Компания Уилкокс (2007). Steam, его создание и использование. Урбана, Иллинойс: Проект Гутенберг. Получено https://www.gutenberg.org/cache/epub/22657/pg22657-images.html.

Эта электронная книга предназначена для использования кем угодно и где угодно, бесплатно и практически без каких-либо ограничений. Вы можете скопировать ее, отдать или повторно использовать в соответствии с условиями лицензии Project Gutenberg, включенной в данную электронную книгу или на сайте www.gutenberg.org< /a>, расположенный по адресу https://www.gutenberg.org/policy/license.html.. эм>