
Изучение аргументов поиска
23 декабря 2022 г.TL;DR
Как упоминалось в предыдущей статье Здравствуйте, OlaVM!, цель OlaVM – построить высокопроизводительную ZKVM, и в этой статье речь пойдет об одном из инструментов, делающих OlaVM высокопроизводительным, а именно о Lookup Arguments. Аргументы поиска играют важную роль в уменьшении размера схемы, тем самым повышая эффективность нулевого разглашения, и он широко используется при проектировании схем ZKVM. В этой статье вы узнаете больше о следующем:
- Какую роль играют аргументы поиска в ZKVM? Принципы
- протокола поиска
- протокол поиска аргументов принцип Halo 2
- Связь между двумя алгоритмами поиска аргументов
Роли ZKVM
ZKVM использует нулевое разглашение для ограничения всех процессов выполнения виртуальной машины, а процесс выполнения виртуальной машины обычно можно разделить на выполнение инструкций, доступ к памяти и выполнение встроенных функций. Несколько непрактично выполнять ограничения на эти операции в одной трассе. Во-первых, в трассировке строка представляет тип операции, и один тип операции соответствует нескольким ограничениям, а разные ограничения соответствуют разному количеству столбцов, что приводит к разной ширине. Если одна из строк слишком широка из-за одного ограничения, соответствующего слишком большому количеству столбцов, это влияет на ширину всей трассы, которая становится слишком большой. Использование ресурсов при таком дизайне является расточительным, когда строки, соответствующие остальным ограничениям, не требуют большого количества столбцов. Затем, если в одной трассе слишком много разных типов операций, будет введено больше селекторов, что увеличит не только количество полиномов, но и порядок ограничения. Наконец, из-за ограничения порядка группы количество строк самой трассы не может превышать порядок группы, поэтому количество строк трассы, занимаемых определенным типом операции, должно быть сведено к минимуму.
Итак, для простоты нам нужно:
- Разделите различные типы операций на несколько вложенных трассировок и проверьте их по отдельности, при этом согласованность данных между основной трассировкой и вложенными трассировками должна обеспечиваться аргументом поиска.
2. Для некоторых неблагоприятных для ZK вычислений мы можем уменьшить размер трассировки с помощью методов Lookup Argument, таких как побитовые операции. n Конечно, есть и другие технические средства для уменьшения размера трассировки, и они будут объяснены далее в этой статье.
Поиск между таблицами трассировки
Все процессы выполнения ВМ будут формировать полную трассировку, называемую «основной трассировкой». «Полный» означает, что он содержит все состояния выполнения ВМ, но не вспомогательные состояния, такие как некоторая расширенная информация, удобная для проверки ЗК. Как упоминалось ранее, включение этой вспомогательной информации в основную трассу сделает основную трассу сложной и трудной для ограничения. Поэтому для удобства ограничений обычно устанавливаются некоторые подтрассы, а затем для этих подтрасс соответственно накладываются ограничения, а основные трассы в основном используются для выполнения корректных программных ограничений и контекстных ограничений.

Создавая различные вложенные трассировки, мы разделяем различные операции, выполняемые виртуальной машиной, и гарантируем, что данные во вложенной трассировке получены из основной трассировки с помощью методов аргумента поиска. Для подтверждения достоверности данных во вспомогательной трассировке необходимо создать различные трассировки в соответствии с конкретным типом операции, а затем использовать соответствующие ограничения для подтверждения достоверности этих трассировок. В частности, для недружественных к zk операций, таких как Bitwise и rangecheck.
Поиск недружественных ZK операций
Как упоминалось ранее, доказательства каждой подтрассы независимы, поэтому получение наименьшей возможной трассы повысит эффективность доказывающего. Взяв в качестве примера побитовые операции, побитовые операции включают AND, XOR и NOT. Если вы просто хотите реализовать ограничения побитовых операций через схемы, вам может потребоваться разбить каждую OP на несколько двоичных ветвей, и если эти OP имеют ширину 32 бита, они будут разделены на 32 ветви. Затем вам нужно ограничить это:
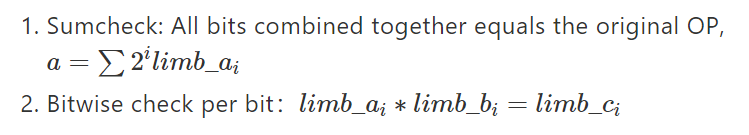
Всего 2+323=99 ячеек трассировки, а число ограничений равно 3 * проверка суммы +33 побитовое значение = 35.
Если в настоящее время существуют таблицы истинности для вычислений AND, XOR и NOT, вы можете определить три таблицы, содержащие данные для побитовых вычислений, которые относятся к операции с заданной битовой шириной, например 8-битной. Для 32-битных операций вам нужно только разбить их на четыре 8-битных ветви, и тогда побитовое отношение между этими ветвями OP не нужно реализовывать с соответствующими ограничениями, нужно только выполнить Lookup на фиксированной таблице. В настоящее время используется 3+4*3=15 ячеек трассировки с 3 суммами ограничений и одним аргументом поиска (поддерживается пакетный поиск).
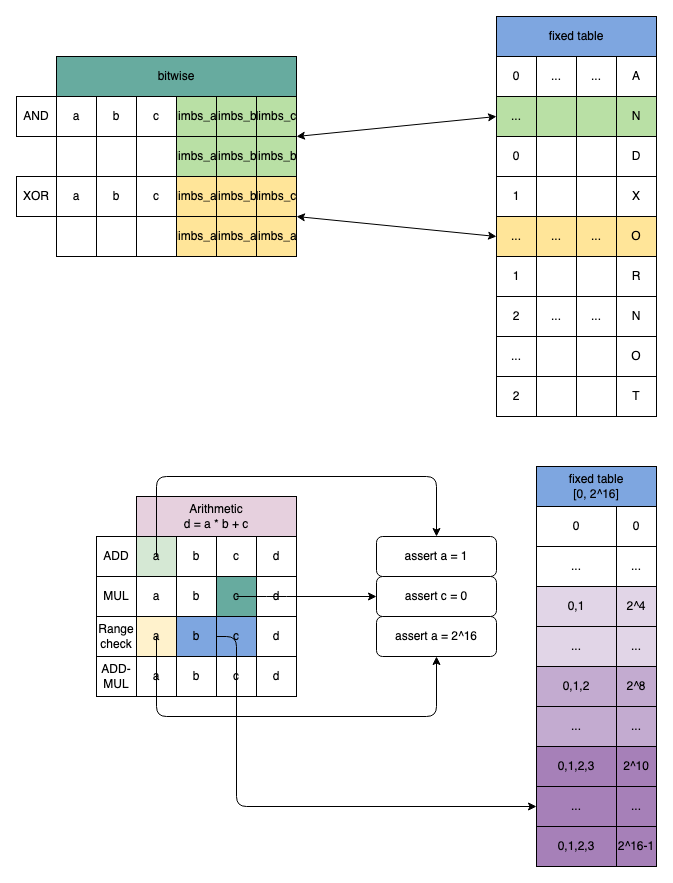
Использование аргументов поиска дает огромный толчок не только для проверки побитовых операций, но и для операций проверки диапазона. Для 32-битной OP вам нужно всего лишь разделить ее на две 16-битные ветви. Здесь есть два хороших дизайна. Во-первых, это позволяет проверке диапазона занимать меньше ячеек трассировки, а во-вторых, наше специальное ограничение ADD-MUL можно повторно использовать для ограничения суммы проверки диапазона. Для различных типов вычислений возможность повторного использования одного и того же ограничения очень помогает повысить общую эффективность. Как показано на рисунке выше, настраиваемый вентиль ASS-MUL может поддерживать повторное использование ограничений пяти типов вычислений: ADD, MUL, ADD-MUL, EQ и RANGECHECK.
Протокол поиска
Plookup — это протокол, используемый для проверки того, что многочлен
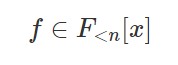
порядка меньше n значение мультипликативной группы H порядка n содержится в d-мерной таблице F^d. Типичным сценарием является проверка диапазона в zk-snark, проверяющая, что значения всех полиномов над H находятся на [0, m].
Описание символа

Предварительная обработка

Процесс протокола


Понимание протокола
- Определите два полинома F и G:
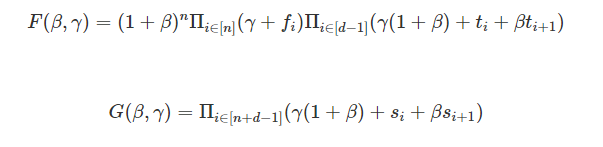
где F ≡ G, d = n + 1, тогда и только тогда, когда:
- f ⊂ т
- s — порядок (f, t) относительно t .
Это переводит доказательство f ⊂ t в доказательство F ≡ G, которое должно доказать, что s является перестановкой (f , т).
Докажите, что a、b является необходимым условием для того, чтобы F ≡ G было истинным:
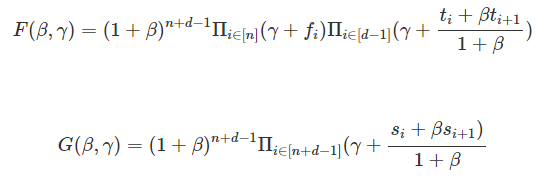

- Что такое Z от PP при расчете

- Что проверяет V:
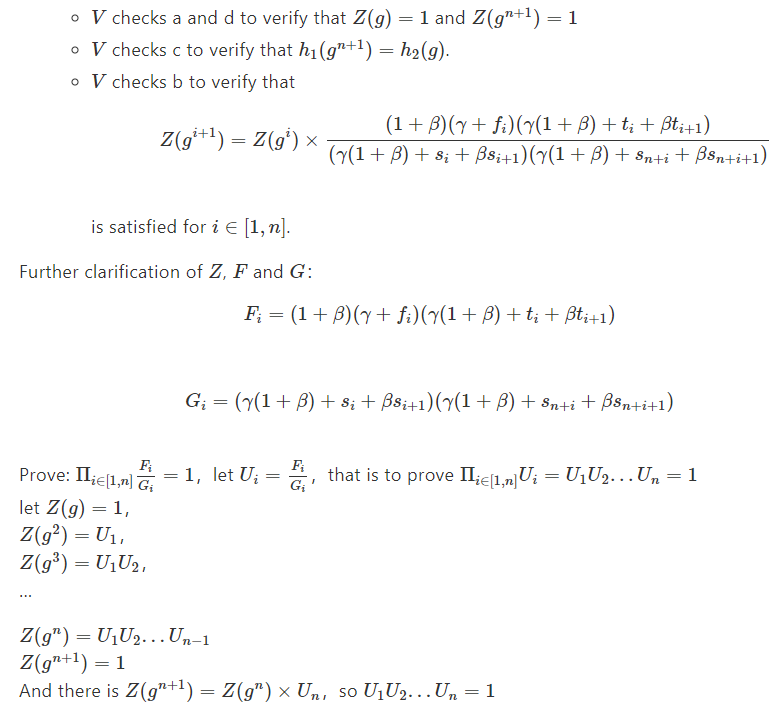
Протокол поиска Halo2
Введение
Функция протокола поиска Halo2 состоит в том, чтобы, учитывая два столбца данных A и S с длиной 2^k, доказать, что каждая ячейка в A находится в S, и некоторые ячейки в S не могут быть в A, и
- S может быть фиксированным или переменным.
- Случай, когда S является переменной, заключается в включении столбцов в трассировку, а значения не являются фиксированными.
- A и S могут содержать повторяющиеся данные, и если размер A и S не достигает 2^k, их нужно дополнить до 2^k.
- Заполните A некоторыми данными из S.
- Заполните S последними данными.
Процесс протокола
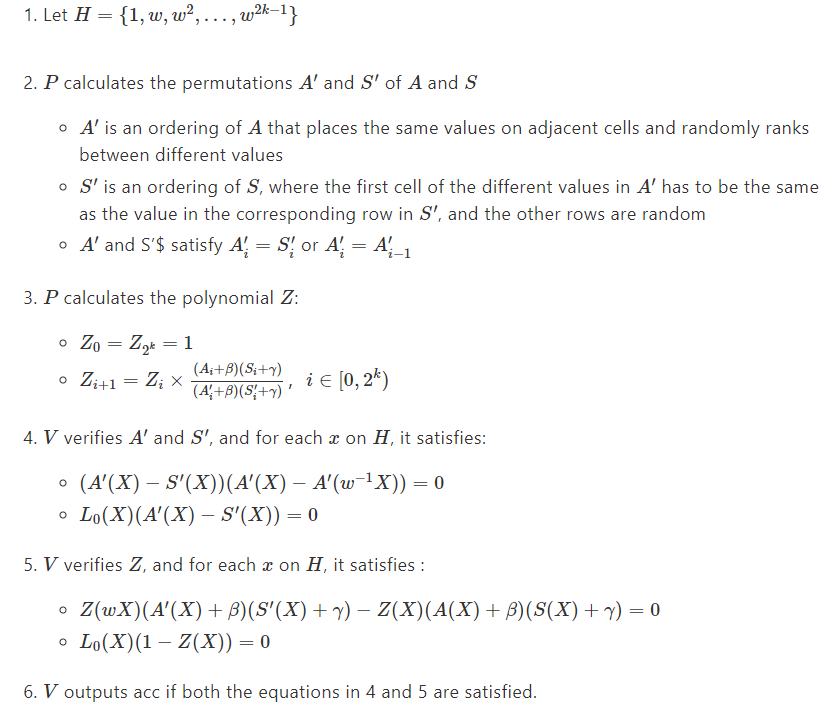
Протокол проверяет только расширенную связь между A и S. Как гарантируется, что расширение действительно для S?
Предположим, что A = {1,2} и S = {3,4}, оба из которых не удовлетворяют аргументу подмножества, расширяются до A = {1,2,3,4} и S = {1,2, 3,4}, что может быть оправдано аргументом подмножества.
Это необоснованно, но как доказать, что это действительно так?
Поддержите ZK

Расширить - 1: Поиск вектора

Расширить – 2: несколько таблиц

Сравнение Plookup и Lookup

Также опубликовано здесь.
Оригинал

