Изучение обхода графа: от поиска в ширину до алгоритма Дейкстры
15 марта 2023 г.Если вы знаете об алгоритме поиска в ширину, и даже если не знаете, вы сможете легко понять алгоритм Дейкстры, который мы рассматриваем в этой статье.
Поиск диаграммы в ширину
Первый алгоритм, который я хотел бы описать, — это поиск в ширину график.
Что это?
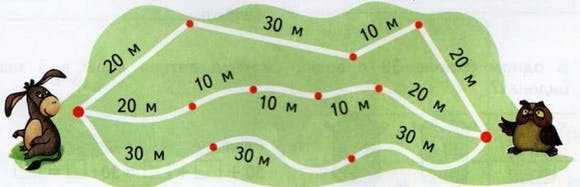
Отступим от формального описания графов и представим себе картину. Раскладываем на земле веревки, пропитанные чем-то легковоспламеняющимся, одинаковой длины так, чтобы ни одна из них не пересекалась, но некоторые из них касались друг друга концами. А теперь зажигаем один конец.
Как будет вести себя огонь?
Он будет равномерно распространяться по веревкам на соседние перекрестки, пока все не загорится. Эту картину легко обобщить на трехмерное пространство. Вот как будет выглядеть поиск в ширину графа в реальной жизни.
Теперь опишем его более формально. Начнем поиск в ширину с некоторой вершины V. В следующий момент времени проверим соседей вершины V (сосед вершины V — это вершина, имеющая общее с V ребро). И так далее, пока не будут просмотрены все вершины графа.
Реализация поиска в ширину
Предположим, что мы находимся в некоторой вершине в процессе поиска в ширину. Затем мы будем использовать очередь, в которую будем добавлять всех соседей вершины, кроме тех, которые мы уже посетили.
void bfs(int u) {
used[u] = true;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i];
if (!used[v]) {
used[v] = true;
q.push(v);
}
}
}
}
В этой реализации g — это список смежности, т. е. g[u] содержит список вершин, смежных с u (в качестве списка используется std::vector), а used — это массив, позволяющий понять, какие вершины у нас уже есть. посетил.
Здесь поиск в ширину ничего не делает, кроме самого поиска. Это может показаться ненужным, но его можно легко изменить, чтобы найти то, что нам нужно, например расстояние и путь от любой вершины до всех остальных. Следует отметить, что ребра не имеют весов, т.е. граф невзвешенный. Вот реализация поиска расстояний и путей.
void bfs(int u) {
used[u] = true;
p[u] = u;
dist[u] = 0;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i];
if (!used[v]) {
used[v] = true;
p[v] = u;
dist[v] = dist[u] + 1;
q.push(v);
}
}
}
}
Здесь p — массив предков, т. е. p[v] — предок вершины v, а dist[v] — расстояние от начальной вершины обхода до вершины v. Как восстановить путь? Это довольно легко сделать, просто пройдясь по массиву предков нужной вершины. Например, рекурсивно:
void print_way(int u) {
if (p[u] != u) {
print_way(p[u]);
}
cout << u << ' ';
}
Кратчайшие пути
Все дальнейшие рассуждения будут справедливы только в том случае, если веса ребер неотрицательны. Теперь давайте перейдем к взвешенным графам, где ребра графа имеют вес, такой как длина ребра, плата за его прохождение или время, необходимое для прохождения через него. Задача состоит в том, чтобы найти кратчайший путь из одной вершины в другую. В этой статье я начну с поиска в ширину и не припомню, чтобы где-либо еще встречал такой подход. Может быть, я пропустил это. Итак, давайте еще раз взглянем на реализацию поиска в ширину, особенно на условие добавления в очередь.
При поиске в ширину мы добавляем в очередь только те вершины, в которых еще не были. Теперь изменим это условие и добавим те вершины, расстояние до которых можно уменьшить. Очевидно, что очередь будет пустой только тогда, когда не останется вершин, расстояние до которых можно уменьшить. Процесс сокращения пути из вершины V называется релаксацией вершины V.
Следует отметить, что изначально путь ко всем вершинам равен бесконечности (в качестве бесконечности возьмем некоторое достаточно большое значение, а именно такое, что ни один путь не будет иметь длину больше значения бесконечности). Этот алгоритм непосредственно следует из поиска в ширину, и это был первый алгоритм, который я придумал, решая свою первую задачу поиска кратчайших путей в графе. Стоит отметить, что этот метод находит кратчайшие пути от вершины, с которой мы начали алгоритм, ко всем остальным.
Вот реализация:
const int INF = 1e+9;
vector< pair<int, int> > g[LIM]; // In g[u] there is a list of pairs: (the length of the path between vertex u and v, vertex v).
void shortcut(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
queue<int> q;
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i].second, len = g[u][i].first;
if (dist[v] > dist[u] + len) {
p[v] = u;
dist[v] = dist[u] + len;
q.push(v);
}
}
}
}
Почему мы храним такие пары в списке смежности? Это станет ясно чуть позже, когда мы усовершенствуем этот алгоритм, но, честно говоря, для этой реализации пары можно хранить наоборот. Мы можем немного улучшить процесс вставки в очередь, введя логический массив, чтобы отметить, находится ли вершина, которую нужно ослабить, в очереди.
const int INF = 1e+9;
vector< pair<int, int> > g[LIM];
bool inque[LIM];
void shortcut(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
queue<int> q;
q.push(u);
inque[u] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
inque[u] = false;
for (int i = 0; i < (int) g[u].size(); i++) {
int v = g[u][i].second, len = g[u][i].first;
if (dist[v] > dist[u] + len) {
p[v] = u;
dist[v] = dist[u] + len;
if (!inque[v]) {
q.push(v);
inque[v] = true;
}
}
}
}
}
Если присмотреться, этот алгоритм очень похож на алгоритм Левита, но это не то же самое, хотя в худшем случае он имеет ту же асимптотическую сложность. Сделаем грубую оценку этого. В худшем случае нам придется выполнять релаксацию каждый раз, когда мы проходим через любое ребро. Итого O(n * m). Смета довольно приблизительная, но для начального этапа достаточно. Также стоит отметить, что это наихудший сценарий, и на практике даже такая реализация работает довольно быстро.
А теперь самое интересное!... Барабанная дробь... Усовершенствуем наш алгоритм до алгоритма Дейкстры!
Алгоритм Дейкстры
Первая оптимизация, которая приходит на ум, заключается в ослаблении только тех вершин, чей текущий путь минимален. Эта идея пришла мне в голову в один прекрасный день, но, как оказалось, я был далеко не первым. Замечательный ученый Эдсгер Дейкстра первым пришел к этой идее.
Более того, он доказал, что, выбирая таким образом вершины для релаксации, мы проведем релаксацию не более n раз! Интуитивно понятно, что если путь к некоторой вершине на данный момент минимален, мы не можем сделать его еще меньше. Вы можете прочитать об этом в Википедии.
Теперь осталось только понять, как эффективно найти вершину с минимальным расстоянием до нее. Для этого мы будем использовать приоритетную очередь (кучу). В STL есть класс, который его реализует и называется priority_queue. Я приведу реализацию, которая, опять же, напрямую следует из предыдущего (описанного в этой статье) алгоритма.
void dijkstra(int u) {
fill(dist, dist + n, INF);
dist[u] = 0;
p[u] = u;
priority_queue< pair<int, int>, vector< pair<int, int> >, greater< pair<int, int> > > q;
q.push(make_pair(0, u));
while (!q.empty()) {
pair<int, int> u = q.top();
q.pop();
if (u.first > dist[u.second]) continue;
for (int i = 0; i < (int) g[u.second].size(); i++) {
int v = g[u.second][i].second, len = g[u.second][i].first;
if (dist[v] > dist[u.second] + len) {
p[v] = u.second;
dist[v] = dist[u.second] + len;
q.push(make_pair(dist[v], v));
}
}
}
}
Скорее всего, не совсем понятно, что здесь происходит. Итак, начнем с объявления приоритетной очереди.
Здесь первый аргумент шаблона — это данные, хранящиеся в очереди, а именно пары вида (расстояние до вершины, номер вершины). Второй аргумент шаблона — контейнер, в котором будут храниться данные, а третий аргумент — компаратор (который, кстати, находится в функциональном заголовочном файле).
Зачем нужен другой компаратор?
Поскольку со стандартным объявлением priority_queue< пара<целое, целое> >, мы сможем извлечь только вершины с максимальным расстоянием, тогда как на самом деле нам нужно обратное. Асимптотическая сложность этого решения задачи составляет O(n * log(n) + m * log(n)).
Действительно, у нас есть только n релаксаций, и мы можем найти вершину с минимальной длиной пути к ней за log(n) времени (что является асимптотической сложностью стандартной реализации очереди с приоритетами в STL).
Следует также отметить, что мы можем в конечном итоге добавить одну и ту же вершину в очередь с разными путями к ней. Например, мы могли релаксировать от вершины A, соседом которой является вершина C, а затем релаксировать с вершины B, соседом которой также является вершина C. Чтобы избежать проблем, связанных с этим, мы просто пропускаем вершины, которые мы извлекли из очереди, но чье расстояние от очереди уже не актуально, т.е. больше, чем текущий кратчайший путь. Вот почему реализация включает строку «if (u.first > dist[u.second]) continue;».
Заключение
Оказывается, на самом деле очень легко реализовать алгоритм Дейкстры с временной сложностью O(n * log(n) + m * log(n)).
Оригинал

