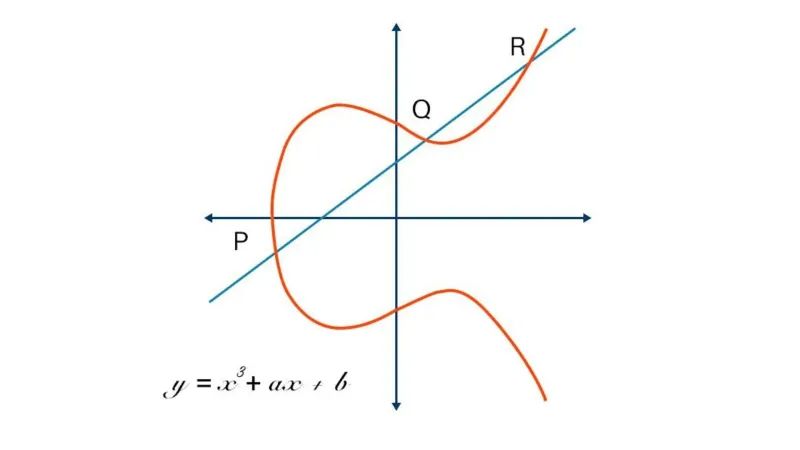
Криптография на основе эллиптических кривых: основное введение

Криптография на эллиптических кривых: базовое введение

Криптография на эллиптических кривых (ECC) — это современная методика [шифрования с открытым ключом] (https://searchsecurity.techtarget.com/definition/public-key), известная тем, что она меньше, быстрее и эффективнее, чем традиционные. Биткойн, например, использует ECC в качестве своей асимметричной криптосистемы, потому что она очень легкая. Математическая сущность, которая делает все это возможным, — это эллиптическая кривая, поэтому читайте дальше, чтобы узнать, как эти кривые позволяют реализовать некоторые из самых передовых [криптографий] (/cryptography/what-is-cryptography/) в мире.

Для чего используется криптография на основе эллиптических кривых?

Обычно ECC используется для шифрования данных, чтобы их могли расшифровать только авторизованные стороны. Это имеет несколько очевидных вариантов использования, но чаще всего используется для шифрования интернет-трафика.

Например, в веб-приложении boot.dev я мог бы использовать ECC для шифрования электронного письма с подтверждением, чтобы никто, кроме получателя, не мог прочитать сообщение.

ECC — это криптография с открытым ключом

Существует множество типов криптографии с открытым ключом, и криптография на основе эллиптических кривых — это всего лишь один из вариантов. Другие алгоритмы включают RSA, Diffie-Helman, и т.д.

Давайте кратко рассмотрим криптографию с открытым ключом в качестве отправной точки, чтобы я мог обсудить ECC и развить эти идеи. Во что бы то ни стало, изучите более подробно криптографию с открытым ключом, когда у вас будет время.

Криптография с открытым ключом позволяет:

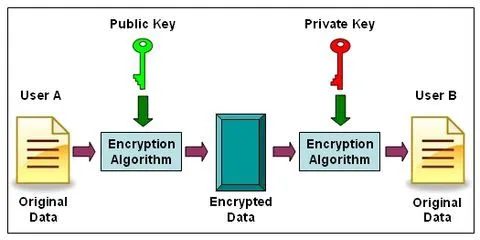
Мы создаем два ключа, открытый ключ и закрытый ключ. Открытый ключ предоставляется бесплатно, и любая сторона может зашифровать данные с его помощью. Однако закрытый ключ держится в секрете, и только те, у кого он есть, смогут расшифровать данные.

Пример криптографии с открытым ключом

Давайте представим, что Facebook собирается получить приватный пост от Дональда Трампа. Facebook должен быть в состоянии гарантировать, что, когда экс-президент отправляет свой пост через Интернет, никто посередине (например, АНБ или интернет-провайдер) не сможет прочитать сообщение. Весь обмен с использованием криптографии с открытым ключом будет выглядеть следующим образом:

• Дональд Трамп уведомляет Facebook, что хочет отправить им личный пост

• Facebook отправляет Дональду Трампу свой открытый ключ

• Дональд Трамп использует открытый ключ для шифрования своего поста:

"Я люблю Fox and Friends" + открытый ключ = "s80s1s9sadjds9s"

• Дональд Трамп отправляет в Facebook только зашифрованное сообщение

• Facebook использует свой закрытый ключ для расшифровки сообщения:

“s80s1s9sadjds9s” + закрытый ключ = “Я люблю Fox and Friends”

Как видите, эта форма шифрования может быть весьма полезной. Вот некоторые ключевые моменты:

• Открытый ключ можно безопасно отправить кому угодно. Это общедоступно.

• Закрытый ключ должен храниться в безопасности, потому что, если кто-то посередине получит закрытый ключ, он сможет расшифровать сообщения.

• Компьютеры могут быстро использовать открытый ключ для шифрования сообщения и быстро использовать закрытый ключ для расшифровки сообщения.

• Компьютерам требуется очень долгое время (миллионы лет) для получения исходных данных из зашифрованного сообщения, если у них нет закрытого ключа.

Как это работает: функция люка

Суть всех криптографических алгоритмов с открытым ключом в том, что каждый из них имеет свою уникальную функцию «лазейки». Функция-лазейка — это функция, которая может быть вычислена только одним способом или, по крайней мере, может быть вычислена только одним способом легко (менее чем за миллионы лет с использованием современных компьютеров).

Не лазейка:

А + В = С

Если мне даны A и B, я могу вычислить C. Однако, если мне даны B и C, я также могу вычислить A. Это не функция-лазейка.

Функция люка:

"Я люблю Fox and Friends" + открытый ключ --> s80s1s9sadjds9s

Если у меня есть «Я люблю Fox and Friends» и открытый ключ, я могу создать «s80s1s9sadjds9s», но если у меня есть «s80s1s9sadjds9s» и открытый ключ, я не могу создать «I love Fox and Friends».

В RSA, которая, возможно, является наиболее широко используемой криптосистемой с открытым ключом, функция лазейки зависит от того, насколько сложно разложить большие числа на их простые множители.

Открытый ключ: 944 871 836 856 449 473

Закрытый ключ: 961 748 941 и 982 451 653

В приведенном выше примере открытый ключ — это очень большое число, а закрытый ключ — это два основных фактора открытого ключа. Это хороший пример функции лазейки, потому что очень легко перемножить числа в закрытом ключе, чтобы получить открытый ключ, но если все, что у вас есть, это открытый ключ, потребуется очень много времени, используя компьютер, чтобы восстановить его. -создать закрытый ключ.

В реальной криптографии закрытый ключ должен состоять из более чем 200 цифр, чтобы считаться безопасным.

Что отличает криптографию на эллиптических кривых?

Вы бы использовали ECC по тем же причинам, что и RSA. ECC и RSA генерируют открытый и закрытый ключи и позволяют двум сторонам безопасно общаться. Однако одним из преимуществ ECC является то, что 256-битный ключ в ECC обеспечивает примерно такую ​​же безопасность, как и 3072-битный ключ, использующий RSA. ECC позволяет системам с ограниченными ресурсами, таким как смартфоны, встроенные компьютеры и криптовалютные сети, использовать \~10% дискового пространства и пропускной способности, необходимых для RSA.

Функция лазейки ECC

Наверное, поэтому большинство из вас здесь. Функция «лазейка» — это то, что делает ECC особенным и отличным от RSA. Функция люка похожа на математическую игру в бильярд.

Во-первых, мы начинаем с произвольной точки на кривой. Затем мы используем функцию точки, чтобы найти новую точку. Наконец, мы продолжаем повторять функцию точки, чтобы прыгать по кривой, пока, наконец, не окажемся в нашей последней точке. Пройдёмся по алгоритму.

• Начиная с «А»:

• A dot B = -C (Нарисуйте линию от A до B, и она пересечется в -C)

• Отражение по оси X от -C до C

• A dot C = -D (Нарисуйте линию от A до C, и она пересечет -D)

• Отражение по оси X от -D до D

• A dot D = -E (Нарисуйте линию от A до D, и она пересечет -E)

• Отражение по оси X от -E до E

Это отличная функция-лазейка, потому что если вы знаете, где находится начальная точка (A) и сколько прыжков требуется, чтобы добраться до конечной точки (E), найти конечную точку очень легко. С другой стороны, если все, что вы знаете, это где находятся начальная и конечная точки, почти невозможно определить, сколько прыжков потребовалось, чтобы туда добраться.

Открытый ключ: начальная точка A, конечная точка E

Закрытый ключ: количество прыжков от A до E

Ответы на некоторые вопросы по криптографии на эллиптических кривых

Вот несколько вопросов, которые у меня возникли, когда я впервые узнал об ECC. Надеюсь, я смогу правильно их решить.

1. Как находится вторая точка? Если функция точки в основном рисует линию между двумя точками, разве вам не нужна вторая точка для начала?

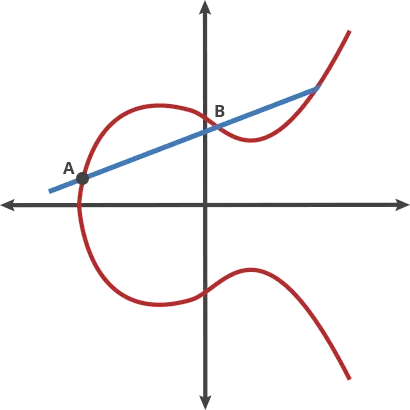
Нет. Вторая точка (мы будем называть ее -R ниже) на самом деле является результатом P точка P (предположим, что первая точка называется P)

P точка P = -R

Так что же такое «P точка P»? На самом деле это просто касательная к P. См. рисунок ниже:

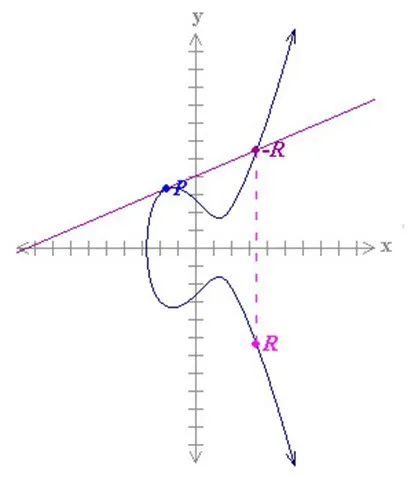
2. Что произойдет, если функция точки создаст линию, которая будет выходить далеко за пределы какой-либо крайности?

Если линия не пересекает кривую близко к началу координат, мы можем фактически определить максимальное значение X, при котором линия будет возвращаться назад и начинаться с самого начала. См. рисунок ниже для примера.

3. Если количество прыжков является закрытым ключом, могу ли я просто считать прыжки, пока не достигну конечной точки?

Неа! Количество прыжков очень велико, что-то вроде 2^256. Было бы слишком долго вычислять каждый переход один за другим, например, p dot p dot p dot p ....

Однако, если вы знаете количество прыжков, вы можете использовать трюк [возведение в степень] (https://en.wikipedia.org/wiki/Exponentiation_by_squaring), чтобы довольно быстро найти конечную точку. Например, опуская детали операций с эллиптическими кривыми: «2P = P точка P», а затем «4P = 2P точка 2P». Это позволяет вам экспоненциально быстрее выполнять эти безумно высокие вычисления.

Какая разница?

ECC используется в качестве алгоритма криптографического ключа в биткойнах, потому что он потенциально может сэкономить \~90% ресурсов, используемых аналогичной системой RSA. Кажется, что каждый год мы видим, как все больше систем переходят от RSA к более современному подходу на основе эллиптических кривых.

Также опубликовано [Здесь] (https://blog.boot.dev/cryptography/elliptic-curve-cryptography/)