Дифференциально частная наука о данных — что, почему и как?

Дифференциальная конфиденциальность стала стандартной структурой для применения строгой защиты индивидуальной конфиденциальности. Она обеспечивает контролируемый способ ввода калиброванного шума в конфиденциальные наборы данных, чтобы любой проведенный статистический анализ соответствовал текущим юридическим требованиям, таким как GDPR или CCPA. Основная идея DP заключается в том, что добавление или удаление любого лица из конфиденциального набора данных не должно существенно влиять на результат анализа. Эта функция обеспечивает надежную гарантию конфиденциальности, позволяя аналитикам и ученым предотвращать атаки на связь, что имеет решающее значение во многих областях, таких как исследования, медицина, перепись и финансы. В этом руководстве мы рассмотрим, как работает эта математическая структура, как ее реализовать, а также важные связанные с этим идеи. В конце мы также рассмотрим некоторые дифференциально-приватные версии игр, таких как Guess Who и Wordle, разработанные для закрепления вашего понимания бюджетов эпсилон и конфиденциальности.

Зачем нам нужна дифференциальная конфиденциальность?

Дифференциальная конфиденциальность использует рандомизированные вычисления для сохранения индивидуальной конфиденциальности. Это означает, что каждый раз, когда вы вычисляете дифференциально частную статистику (например, среднее значение) набора данных, вы получаете другой результат, который близок кистинное значение статистики.

Чтобы сделать каждый результат действительно необратимым, DP вводит калиброванный шум, взятый из распределения вероятностей, обычно распределения Лапласа. Нарисованный шум должен быть достаточно большим, чтобы скрыть присутствие или отсутствие любого отдельного человека в наборе данных, но достаточно малым, чтобы сохранить полезность данных для целей анализа.

Существует несколько сценариев, когда такие меры предосторожности необходимы.

Например, в медицинском исследовании редкого заболевания, если злоумышленник знает общее количество и может узнать, что оно увеличилось на единицу после того, как определенный человек присоединился к исследованию, он может сделать вывод о состоянии здоровья этого человека. Или в базе данных зарплат, если злоумышленник знает среднюю зарплату до и после прихода нового сотрудника, он может потенциально рассчитать точную зарплату этого человека. Другой пример — данные о голосовании: если известен средний возраст избирателей в небольшом округе, а затем он немного меняется после того, как один человек проголосовал, его возраст и избирательный статус могут быть выведены.

Поэтому DP добавляет случайный шум к вычислениям на основе конфиденциальных данных, чтобы гарантировать получение схожих результатов при сравнении наборов данных, отличающихся одной записью.

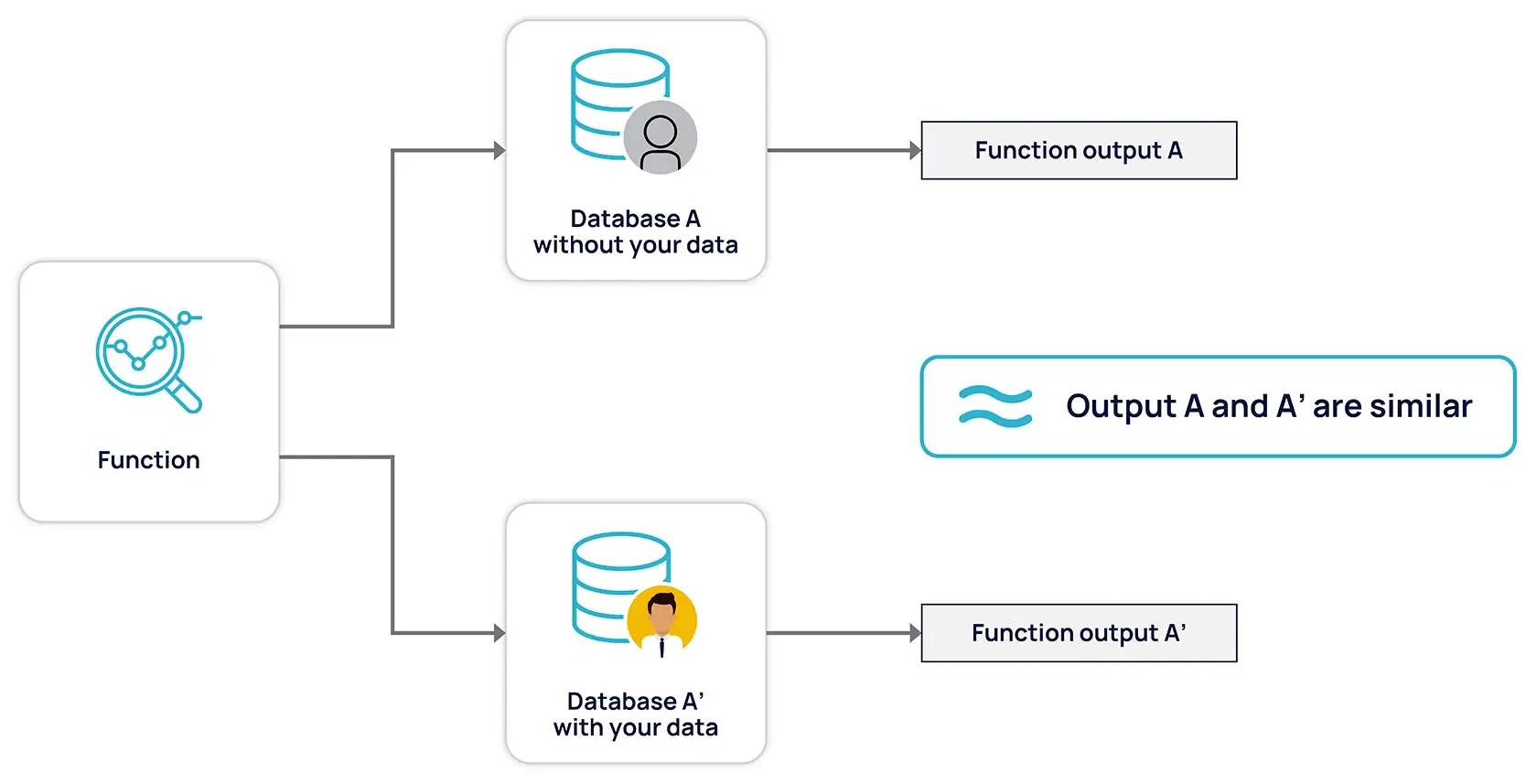
Источник: Анонос

Чувствительность и эпсилон в дифференциальной конфиденциальности

В последнем разделе мы упомянули, что DP вводит шум, извлеченный из распределений вероятностей, в результаты вычислений. Количество этого шума должно быть тщательно откалибровано, чтобы поддерживать пригодность данных к использованию. Например, еслиистинный счетвыборок в наборе данных составляет 1000, частное число не может быть слишком большим, например, 1500, поскольку это сделало бы статистику бесполезной. По этой причине DP использует два критических компонента:чувствительность функцииигиперпараметр эпсилон.

Чувствительность функции — это максимальная величина, на которую может измениться выход функции, если к входу добавляется или удаляется одна единица. Например, чувствительность функции счетчика равна 1, поскольку удаление одной строки из набора данных изменяет выход счетчика только на 1. Эта концепция имеет решающее значение в DP, поскольку чувствительность определяет, сколько шума следует добавить к набору данных. Чем больше чувствительность, тем больше шума необходимо добавить.

Но одной чувствительности недостаточно, потому что нам нужнаэпсилондля управления компромиссом конфиденциальности и полезности. Если мы используем только чувствительность для добавления шума, мы всегда будем добавлять одно и то же фиксированное количество шума независимо от потребностей конфиденциальности.

Однако разные сценарии требуют разных требований к конфиденциальности. Для общенационального общественного опроса с низкими ставками мы могли бы согласиться на меньшую конфиденциальность, добавляя минимум шума. Для конфиденциальных медицинских данных нам нужна более сильная конфиденциальность, требующая большего шума.

DP объединяет чувствительность и эпсилон таким образом, что более низкий эпсилон увеличивает шум, а более высокий эпсилон уменьшает его. Например, при эпсилоне = 1 функция счетчика может добавить шум ±2–3 к истинному счету. Но при эпсилоне = 0,1 (более сильная конфиденциальность) она может добавить шум ±20–30. Эпсилон дает нам эту важную гибкость для настройки защиты конфиденциальности на основе контекста.

Реализация дифференциальной конфиденциальности Epsilon

Теперь давайте конкретизируем теорию, реализовав DP-версии функций счетчика и усреднения:

import numpy as np

def true_counter(data):
    return len(data)

def true_mean(data):
    return np.mean(data)

Сначала мы определяем две функции для нахождения истинной длины и среднего значения набора данных. Теперь давайте реализуемprivate_counterкоторый использует механизм Лапласа (механизм, который вводит шум, извлеченный из распределения Лапласа):

def private_counter(data, epsilon):
    sensitivity = 1
    scale = sensitivity / epsilon
    
    # Draw from Laplace
    noise = np.random.laplace(0, scale)
    private_count = int(true_counter(data) + noise)
    
    return private_count

Thelaplaceфункцияnp.randomМодуль требуетscaleпараметр, который устанавливает якорь в распределении, вокруг которого рисуется шум. Мы вычисляем правильный масштаб, разделив чувствительность на эпсилон. После того, как шум нарисован, мы добавляем шум к истинному счету. Давайте проверим его с различными значениями эпсилон на синтетическом наборе данных с 1000 точек:

# Test private_counter on a synthetic dataset with 1000 points
data = np.ones(1000)

epsilons = [0.1, 1.0, 10.0]
for epsilon in epsilons:
    private_count = private_counter(data, epsilon)
    
    print(f"Epsilon: {epsilon}")
    print(f"True count: {true_counter(data)}")
    print(f"Private count: {private_count}\n")

Вне:

Epsilon: 0.1
True count: 1000
Private count: 997

Epsilon: 1.0
True count: 1000
Private count: 998

Epsilon: 10.0
True count: 1000
Private count: 999

Как мы видим из вывода, при меньшем значении эпсилон (0,1) мы получаем больше шума, добавляемого к истинному счету, что приводит к большей разнице между истинным и частным счетом. По мере увеличения эпсилона (1,0 и 10,0) шум уменьшается, и частный счет приближается к истинному счету 1000.

Теперь давайте реализуемprivate_meanфункция:

def private_mean(data, epsilon):
    # For mean, sensitivity is 1/n since changing one element
    # affects mean by at most 1/n where n is dataset size
    n = len(data)
    sensitivity = 1.0 / n
    scale = sensitivity / epsilon
    
    noise = np.random.laplace(0, scale)
    result = true_mean(data) + noise
    return result

patient_ages = [25, 30, 35, 40, 45, 50, 55, 60]

# Test with different epsilon values
epsilons = [0.01, 0.1, 1]
for epsilon in epsilons:
    priv_mean = private_mean(patient_ages, epsilon)
    print(f"Epsilon: {epsilon}")
    print(f"True mean: {true_mean(patient_ages)}")
    print(f"Private mean: {priv_mean}\n")

Выход:

Epsilon: 0.01
True mean: 42.5
Private mean: 51.35476355418572

Epsilon: 0.1
True mean: 42.5
Private mean: 42.88750141072553

Epsilon: 1
True mean: 42.5
Private mean: 42.507711105508164

Подобно противоположному примеру, мы можем наблюдать, что при меньшем значении эпсилон (0,01) к истинному среднему добавляется больше шума, что приводит к большей разнице между истинным и частным средним. По мере увеличения эпсилон (0,01 и 1) шум уменьшается, а частное среднее приближается к истинному среднему значению возраста пациента. Это демонстрирует компромисс между конфиденциальностью и полезностью в дифференциальной конфиденциальности — более низкий эпсилон обеспечивает более высокую конфиденциальность, но менее точные результаты, в то время как более высокий эпсилон обеспечивает более точные результаты, но более слабые гарантии конфиденциальности.

Важность Эпсилона наглядно продемонстрирована

Весной 2024 года я посетил мероприятие в Оксфордском университете (организованное Oblivious), посвященное исследованиям дифференциальной конфиденциальности, и мне удалось поработать над интересной проблемой: созданием визуализаций дифференциально конфиденциальных данных.

Идея была проста: создать версию DP всех графиков в Matplotlib, чтобы при отображении злоумышленник не мог отследить точки данных до лиц в наборе данных. Эта проблема затем послужила бы двойной цели, показывая визуальный эффект параметра epsilon.

Поскольку Matplotlib предлагает десятки функций построения графиков, для меня и моего коллеги это было невыполнимо,Девьяни Гаури, чтобы воссоздать версии DP для всех графиков за одну неделю. Вместо этого мы придумали хак — дифференциально-частное биннинг гистограмм. С помощью этого метода мы могли воссоздать версию DP любого распределения, а затем продолжать использовать обычные функции Matplotlib для их построения.

Например, рассмотрим эту гистограмму исходного распределения X:

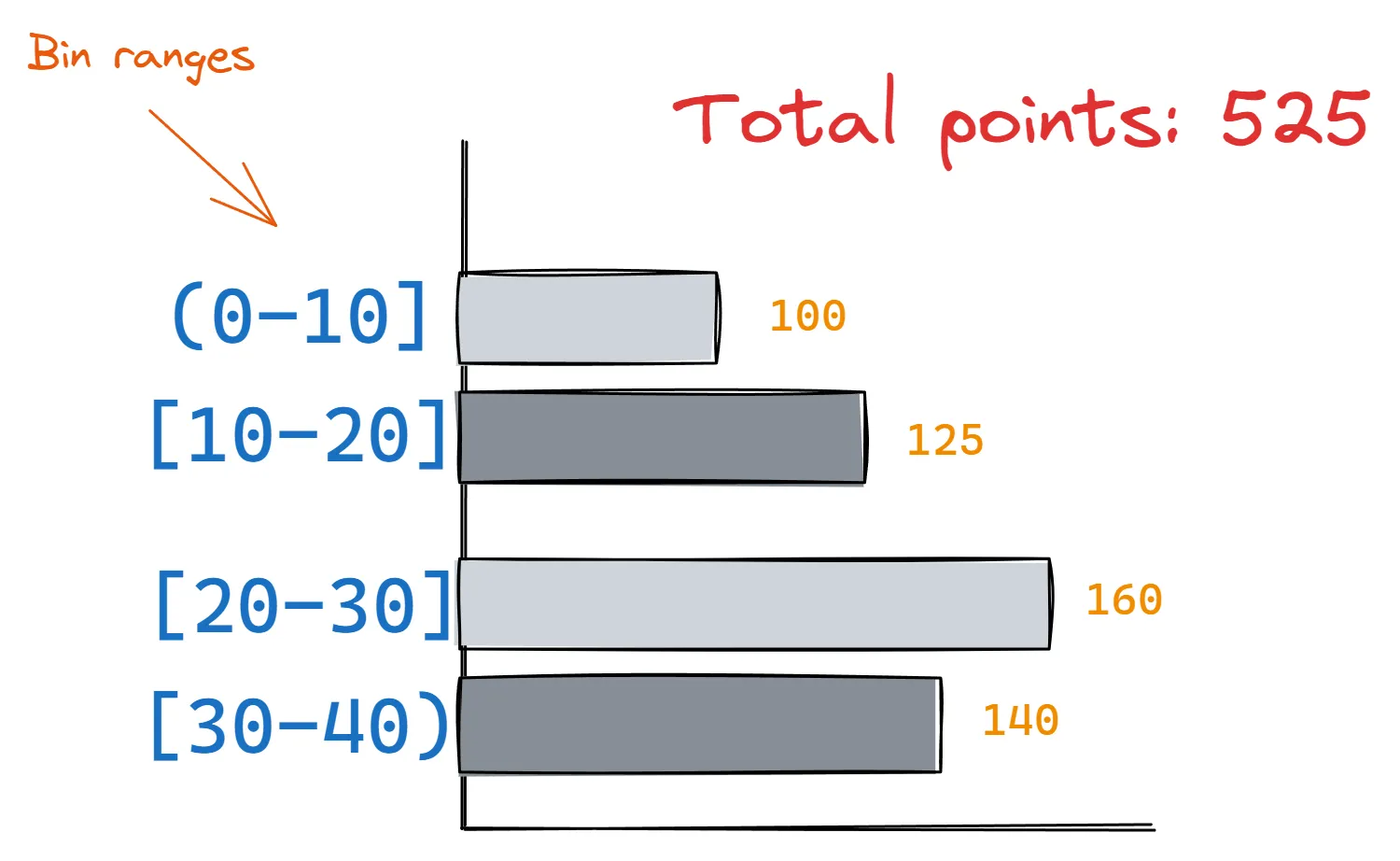
Чтобы создать версию DP этой гистограммы, нам нужно будет только добавить шум Лапласа к каждому счету бинов (мы уже видели, как это сделать). Затем мы можем реконструировать распределение, выбирая случайные точки данных в каждом диапазоне бинов на основе шумных счетов бинов.

Восстановленное распределение будет дифференциально частным, но его гистограмма будет иметь форму, близкую к исходной, исходя из нашего использования эпсилон.

Эта техника оказалась невероятно успешной, и вы можете увидеть результат сами:

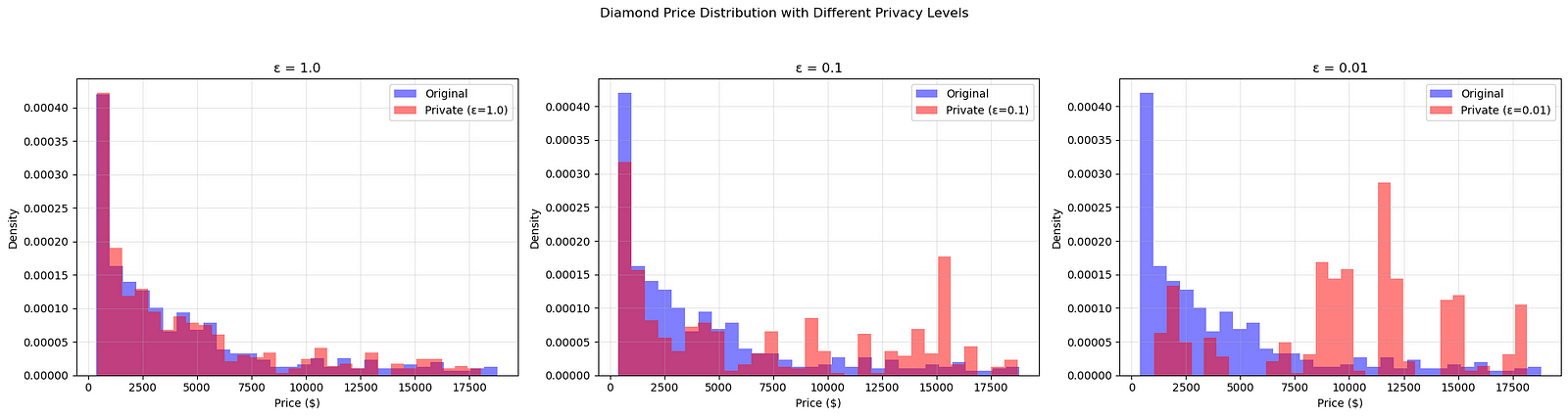
Мы внесли еще несколько изменений в наш подход, но конечный результат тот же: по мере того, как мы уменьшаем эпсилон, гистограмма частного распределения все дальше и дальше отдаляется от оригинала.

А как насчет других графиков? Во время мероприятия мы работали над графиками Kernel Density Estimate, ящиками и диаграммами рассеивания. Подробнее об этой технике можно прочитать вмоя отдельная статья. Вот краткий обзор диаграмм рассеяния, использующих биннинг двумерной гистограммы:

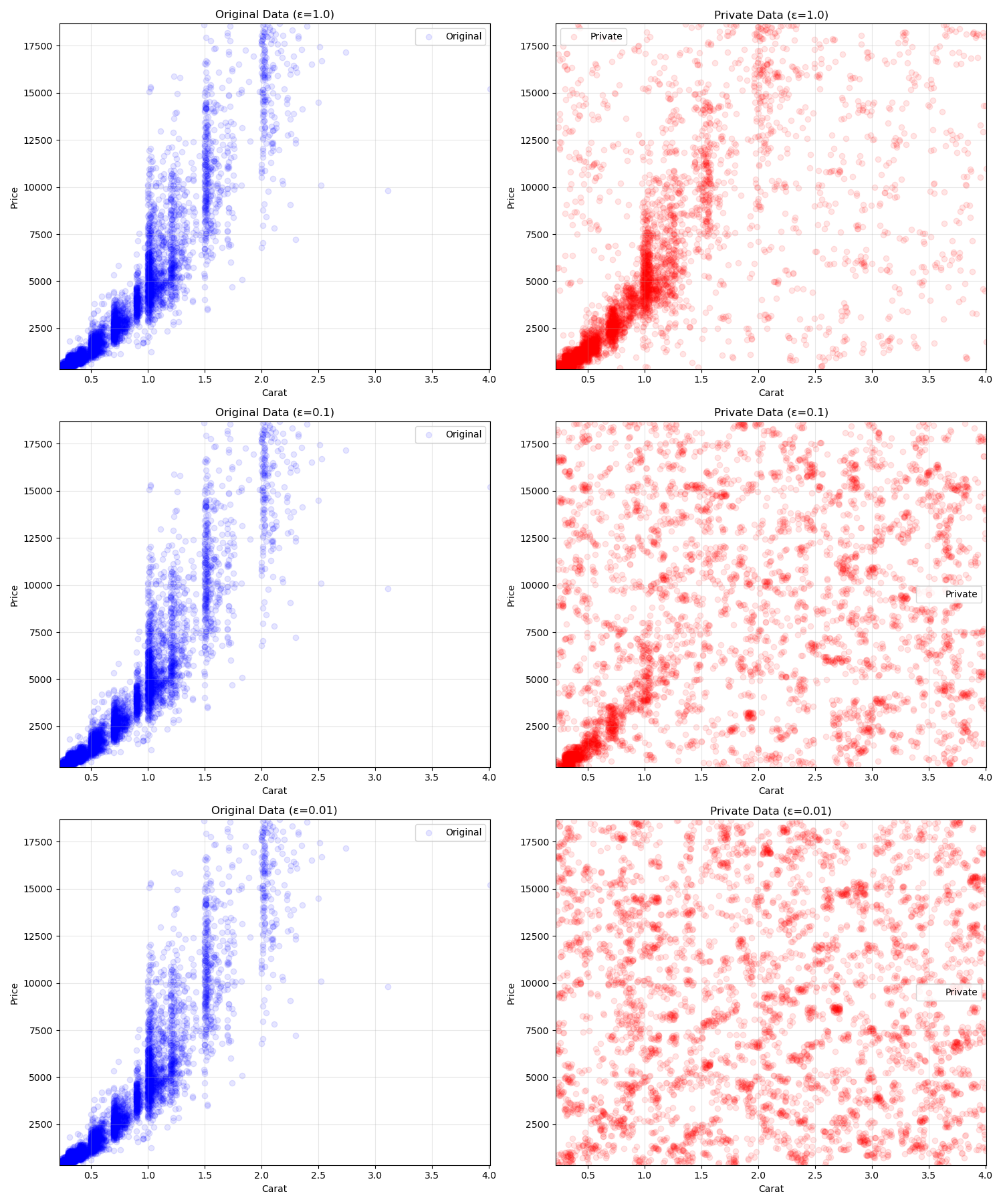
При epsilon=1 общая тенденция исходной диаграммы рассеяния все еще видна, хотя по всему графику есть шум. Но когда мы доходим до epsilon=0,01, распределение полностью разрушается и превращается в хаос.

Чтобы поэкспериментировать с кодом, сгенерировавшим эти графики, вы можете ознакомиться спример блокнотаЯ подготовился.

Бюджет конфиденциальности в дифференциальной конфиденциальности

Еще одной фундаментальной концепцией дифференциальной конфиденциальности являетсябюджет конфиденциальностичто помогает управлять кумулятивной потерей конфиденциальности при выполнении нескольких запросов к конфиденциальному набору данных. Думайте об этом как о банковском счете конфиденциальности — каждый запрос, например, поиск среднего значения или построение гистограммы, «тратит» часть вашего бюджета конфиденциальности, где валюта — эпсилон.

Например:

• Запрос 1 с эпсилоном = 0,1

• Запрос 2 с эпсилоном = 0,3

• Общая потеря конфиденциальности = 0,4

Если ваш общий бюджет конфиденциальности равен 1, вам необходимо тщательно спланировать, как его «тратить», и распределить его между всеми вычислениями, которые вы будете выполнять.

Бюджет конфиденциальности имеет решающее значение по ряду причин. Во-первых, он предотвращает атаки с множественными запросами, когда злоумышленник может сделать много запросов с малыми эпсилонами и объединить результаты для реконструкции конфиденциальных данных. В примере с диаграммой рассеяния можно создать несколько десятков с малыми эпсилонами и наложить их друг на друга (с перекрытием), чтобы максимально приблизиться к исходной диаграмме рассеяния данных.

Команды должны решить, следует ли:

• Делайте меньше запросов с большей точностью (больше ε на запрос)
• Делать больше запросов с меньшей точностью (меньше ε на запрос)
• Сохраните бюджет для будущих важных запросов

Существуют некоторые передовые методы, помогающие более эффективно управлять бюджетами на конфиденциальность. Например, впараллельная композиция, если запросы выполняются на непересекающихся подмножествах данных, их потери конфиденциальности не суммируются. Подход к биннингу гистограммы, который мы описали, использует именно этот метод. Поскольку каждый диапазон бинов гистограммы независим друг от друга, эпсилон не суммируется для всех бинов. Другими словами, использование эпсилон не увеличивается, независимо от того, реконструируете ли вы гистограмму со 100 бинами или 1000.

Вот простой класс, реализующий простой класс бюджета конфиденциальности:

class PrivacyBudget:
    def __init__(self, total_budget):
        self.total_budget = total_budget
        self.spent_budget = 0

    def check_and_spend(self, epsilon):
        if self.spent_budget + epsilon > self.total_budget:
            raise ValueError("Not enough privacy budget remaining!")
        self.spent_budget += epsilon
        return True

    def remaining_budget(self):
        return self.total_budget - self.spent_budget

# Example usage
budget_manager = PrivacyBudget(total_budget=1.0)

# Make multiple queries with different epsilons
data = [25, 30, 35, 40, 45, 50, 55, 60]
epsilons = [0.3, 0.4, 0.2, 0.2]

for i, eps in enumerate(epsilons, 1):
    try:
        budget_manager.check_and_spend(eps)
        result = private_mean(data, eps)
        print(f"Query {i} (ε={eps}): {result:.2f}")
        print(f"Remaining budget: {budget_manager.remaining_budget():.2f}\n")
    except ValueError as e:
        print(f"Query {i} failed: {e}")

Выход:

Query 1 (ε=0.3): 46.57
Remaining budget: 0.70

Query 2 (ε=0.4): 39.19
Remaining budget: 0.30

Query 3 (ε=0.2): 45.37
Remaining budget: 0.10

Query 4 failed: Not enough privacy budget remaining!

Чтобы лучше разобраться в управлении бюджетом на конфиденциальность, я недавно обнаружил некоторыебесплатные игры, в которые можно игратьпредложено Oblivious:

Это DP-вариации некоторых классических и популярных игр, таких как«Угадай кто»или«Слово». Мне особенно нравится «Угадай, кто», потому что в ней на удивление сложно победить из-за дополнительной неопределенности.

В этой версии вам нужно угадать человека, которого выдает ИИ, задавая бинарные вопросы «да/нет». Но вот в чем подвох: в зависимости от выбранного вами эпсилона вероятность честного ответа сильно варьируется.

Например, если установить эпсилон равным 1, вероятность лжи составит 27%:

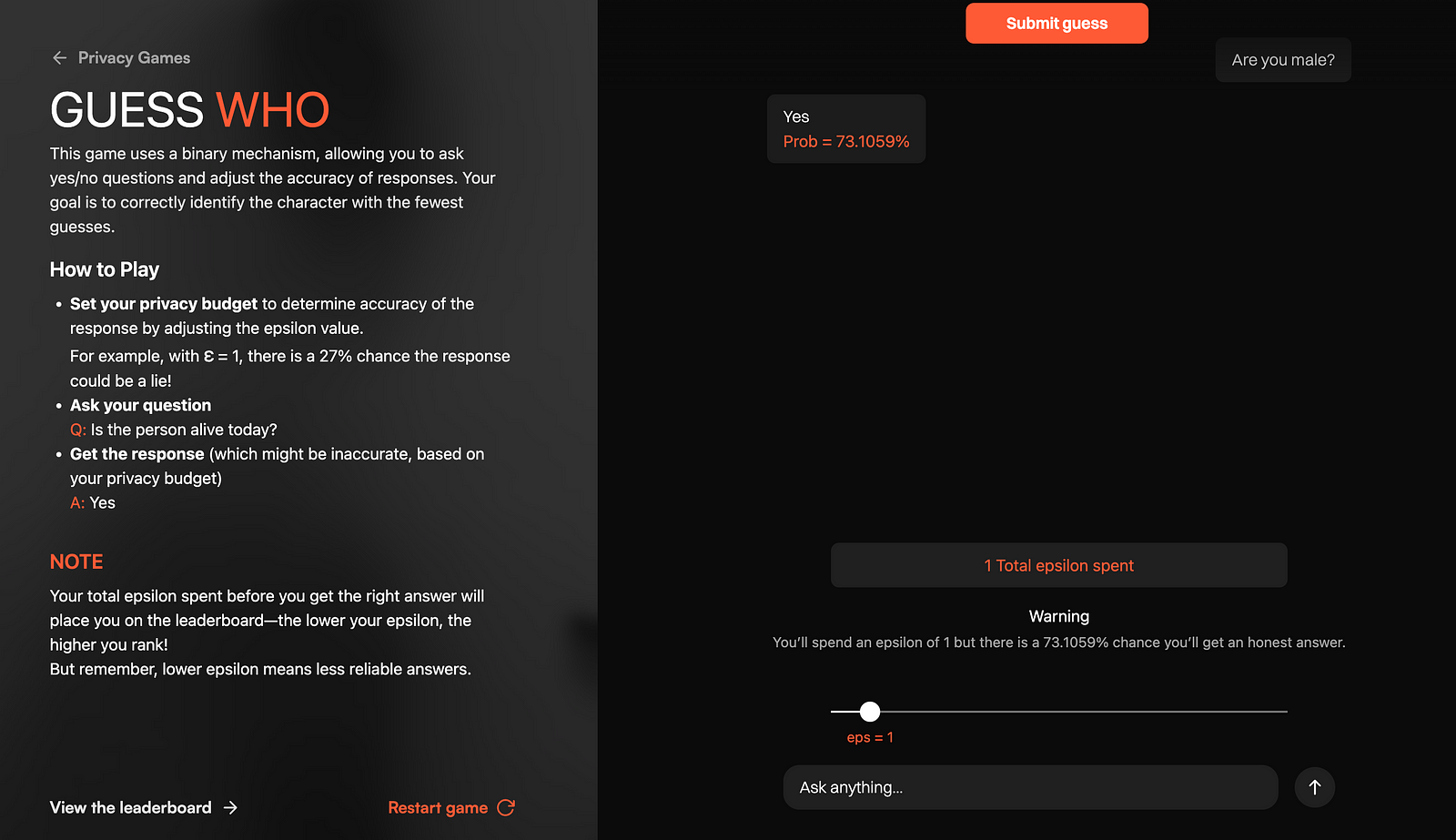
Еще один поворот в том, что вы соревнуетесь с другими игроками, чтобы занять первое место в таблице лидеров. Таким образом, вы не можете просто выиграть игру, установив высокий эпсилон (что практически гарантирует честный ответ каждый раз), и должны думать об общем бюджете, который вы израсходуете.

Чтобы дать вам грубую картину, человек, находящийся в первом месте, нашел ответ за 7 попыток, потратив 8,4 эпсилон, что составляет около 75% вероятности честного ответа на каждый вопрос:

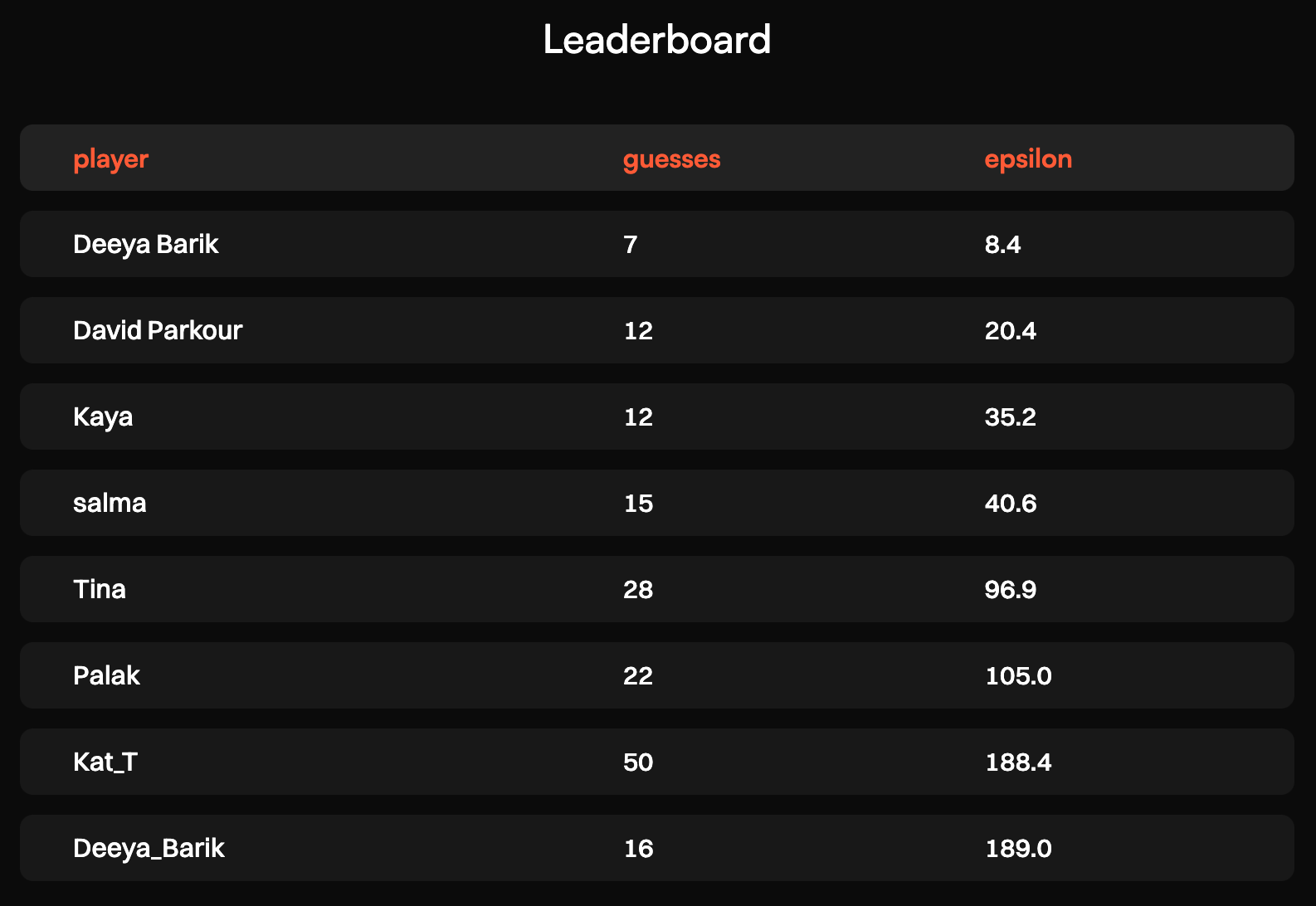
Итак, попробуйте установить свой бюджет на уровне 8 и добиться успеха:

• Задавать много вопросов с низким эпсилоном
• Задайте 3–4 ключевых вопроса с высоким эпсилоном

Что касаетсяWORDPL, это может просто свести вас с ума, потому что вероятность истинной обратной связи для каждой буквы также зависит от эпсилона:

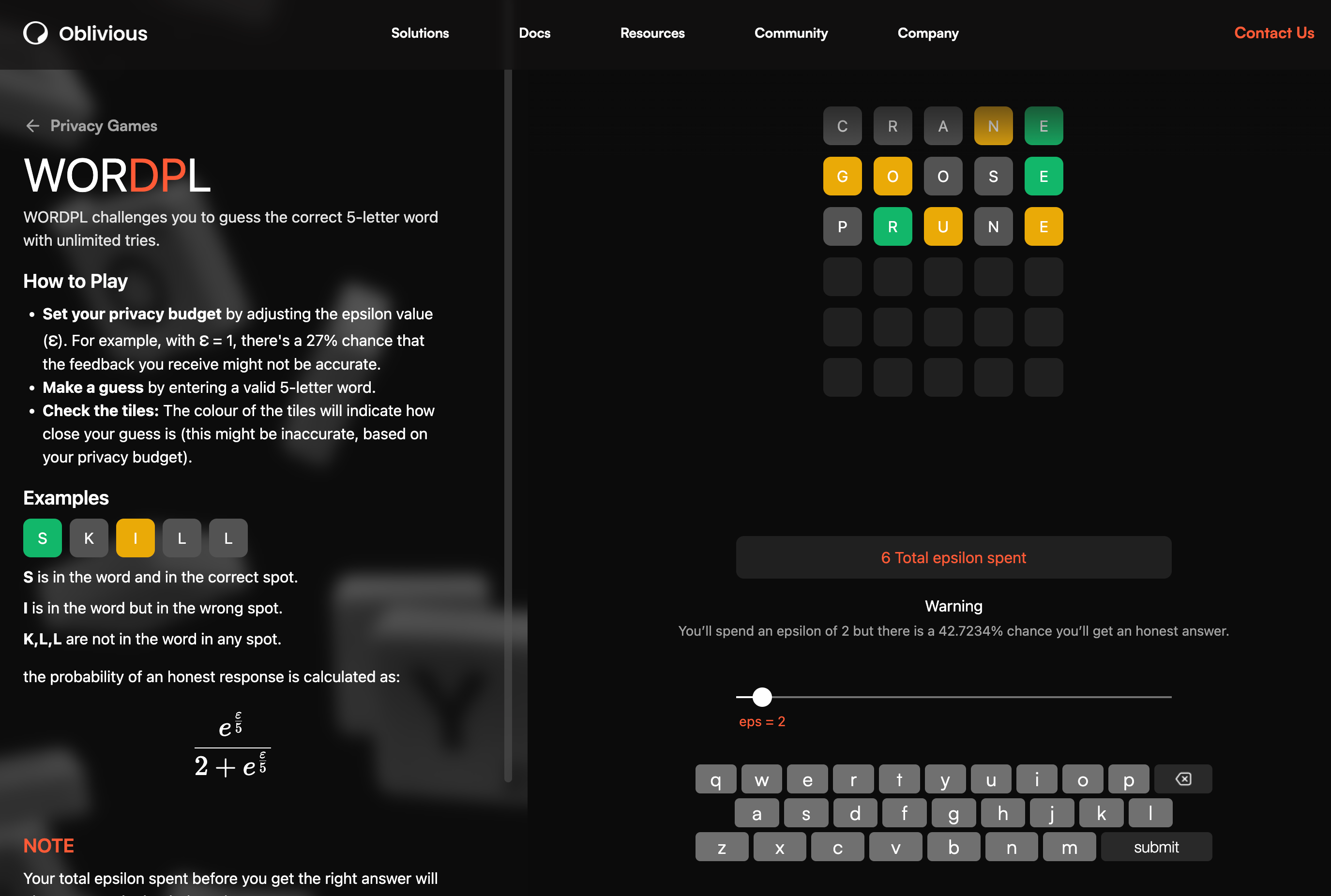
Например, при epsilon=2 существует вероятность ~43%, что буква находится в правильном положении или что в слове есть буквы G, O и N. Я точно знаю, что по крайней мере один из этих отзывов — ложь, потому что я не смог найти ни одного пятибуквенного английского слова, которое быГ, О, Н, иЭв них, которые также заканчиваются наЭ.

В какую бы игру вы ни играли, вы приобретете более глубокое понимание того, как управлять своим бюджетом на конфиденциальность.

Заключение

В этом уроке мы изучили основы дифференциальной конфиденциальности (DP), важной математической структуры для работы с конфиденциальными наборами данных и сохранения индивидуальной конфиденциальности. Мы рассмотрели определение DP, почему оно важно и как реализовать его в Python для некоторых элементарных операций.

В последующих разделах мы более подробно обсудили чувствительность функции и параметры эпсилон, поскольку они имеют решающее значение для вашего понимания DP. Мы завершили разговор о бюджетах конфиденциальности и о том, как лучше их понять, играя в онлайн-игры DP.

Если вы хотите окунуться в этот новый мир открытой науки о данных, вы можете заглянуть сюдаАнтигранулярныйтакже. Это платформа для соревнований, похожая на Kaggle, где вы решаете проблемы DP на реальных наборах данных. Проблема в том, что вам нужно писать код в выделенной среде, где доступно лишь несколько библиотек DP, а наборы данных не видны. Я писал о том, какнавигация по платформев отдельной статье.

Спасибо за чтение!