Защита от атак анализа мощности: предотвращение атак по боковым каналам эллиптической кривой
10 октября 2023 г.В 1999 году Пол Кохер, Джошуа Яффе и Бенджамин Джун написали статью под названием «Дифференциальный анализ мощности». Они описали, как мониторинг питания процессора позволил им определить секретный ключ, связанный с алгоритмом шифрования DES. Это по-прежнему важный атрибут безопасности, о котором следует помнить при разработке современных протоколов. К счастью, для криптографических алгоритмов на основе эллиптических кривых существует математическое решение.
Для проведения атаки на источник питания злоумышленник должен иметь физический доступ к процессору, выполняющему алгоритм. Для смарт-карты это довольно просто. Для приложения на смартфоне потребуется немного больше оборудования. Для большинства приложений об этом стоит беспокоиться.
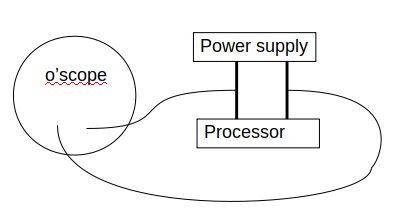
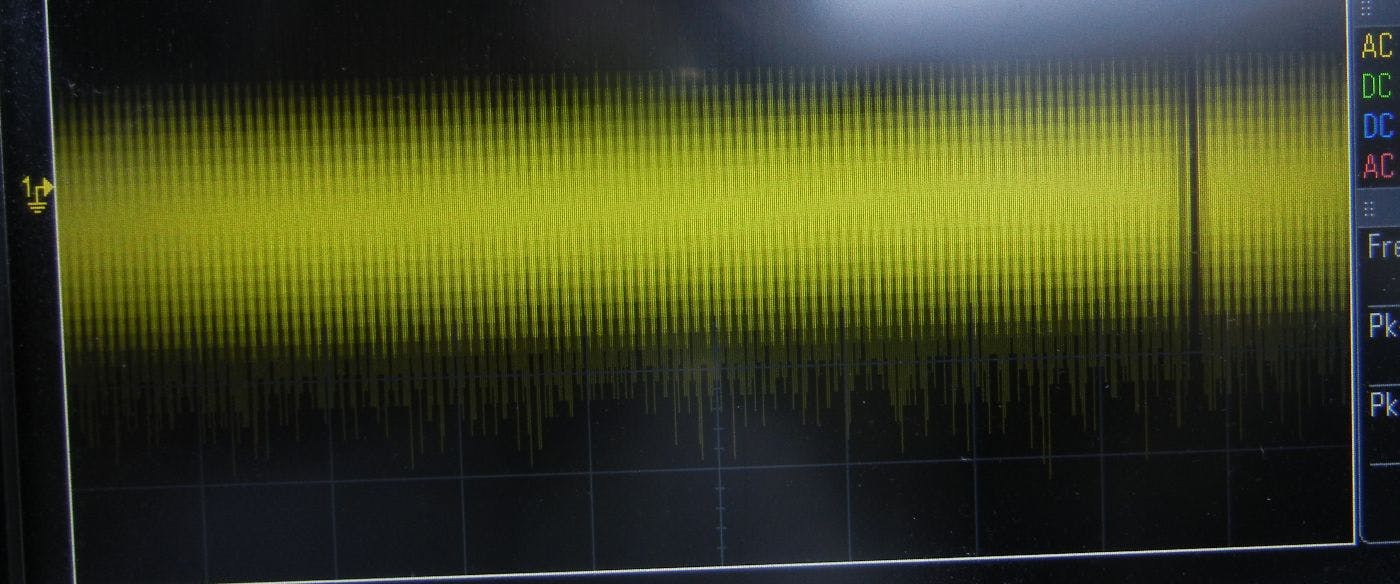
На этом рисунке показана базовая установка для атаки по побочному каналу анализа мощности. У вас есть возможность контролировать напряжение (или ток) от источника питания к процессору. Изменения небольшие, поэтому может быть задействован усилитель, но схема та же. На каждый шаг процессора расходуется разное количество энергии, а некоторые подпрограммы создают на осциллографе определенные шаблоны.
В криптографии эллиптических кривых сложение двух точек имеет определенную формулу. Эта формула может быть более эффективной, если две точки совпадают, что называется удвоением. Классическая формула начисления баллов:
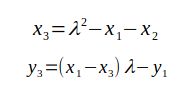
Значения (x_1, y_1) и (x_2, y_2) — это точки, суммируемые вместе. Результат (x_3, y_3) — это новая точка на кривой. Значение лямбды меняется, если добавляемые точки одинаковы или различны. Если точки одинаковы (операция удвоения), значение будет
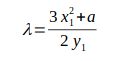
Если точки разные, формула такая
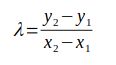
Это различие становится исключительно важным, когда в алгоритме используется закрытый ключ. Процесс умножения включает в себя удвоение для каждой позиции бита, а затем добавление точки, если бит установлен. Вы можете видеть на осциллографе, когда происходит операция удвоения и когда происходит сложение, поэтому вы можете найти закрытый ключ и нарушить безопасность алгоритма эллиптической кривой.
Это плохая проблема. Мы хотим использовать другое значение для лямбды, которое всегда одинаково, независимо от входных точек. Решение — использовать эту формулу.
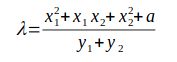
Если x_1 и x_2 одинаковы, мы восстанавливаем формулу удвоения. Единственная проблема заключается в том, что y_1 = -y_2. Это дает точку в бесконечности — и нам приходится иметь дело с этой возможностью независимо от того, какую формулу мы используем.
С точки зрения злоумышленника можно определить количество операций удвоения и сложения. Поскольку простое число, определяющее размер поля, является общедоступным, злоумышленник знает количество битов, используемых для удвоения. Злоумышленник может вычислить количество установленных битов в секретном ключе. Если в простых числах, используемых для обеспечения эллиптической кривой, достаточно битов, будет невозможно угадать, какие биты установлены.
Например, если базовое поле имеет 256 бит для простого числа, а закрытый ключ имеет 128 бит, злоумышленнику необходимо попробовать 2^128 ключей. Это должно соответствовать возрасту Вселенной с помощью большого суперкомпьютера с графическим процессором. Эта формула менее эффективна, чем стандартная версия, но гораздо более безопасна с точки зрения анализа мощности.
Дополнительные сведения о математике эллиптических кривых см. в разделе Криптография эллиптических кривых для разработчиков: http://mng.bz/D9NA.
Оригинал

