Наука о данных для оптимизации портфеля: теория средней дисперсии Марковица

Инвестиционный портфель – это совокупность финансовых активов, таких как акции, облигации или криптовалюта, в которые инвестирует физическое лицо. Инвестиция в основном определяется ее риском (насколько волатильна стоимость) и ее доходностью (какова ожидаемая прибыль). Инвесторы стремятся создать портфель, который минимизирует риск и максимизирует прибыль.

Поскольку суть инвестиций заключается в понимании цифр, опытные трейдеры используют методы и модели анализа данных для оптимизации своей инвестиционной стратегии. Одной из таких моделей является современная теория портфеля (MPT), также известная как теория средней дисперсии Марковица. Модель обеспечивает оптимальный инвестиционный портфель с использованием оценки рисков и максимизирует доход инвестора.

Давайте поймем роль науки о данных в эффективных инвестициях, подробно рассмотрим современную теорию портфеля и обсудим предположения и риски, связанные с моделями науки о данных.

Подробнее о теории средней дисперсии Марковица

Теория средней дисперсии Марковица была впервые опубликована Гарри Марковицем в 1952 году. Теория представляет собой основанную на данных модель, которая анализирует финансовые тенденции для оценки риска и доходности. Как правило, инвестиции подразделяются на низкорисковые, низкодоходные и высокорискованные, с высокой доходностью. Проще говоря, он устанавливает, что инвестиции с более высоким фактором риска приносят более высокую прибыль, и наоборот.

MPT обеспечивает оптимальный выбор инвестиций, который уравновешивает риск и вознаграждение. Окончательный выбор инвестиций и их доли в портфеле представляет собой идеальную инвестиционную стратегию, основанную на тенденциях данных.

Наука, лежащая в основе современной портфельной теории

Давайте разберемся в математике, лежащей в основе MPT. Однако сначала мы должны понять несколько ключевых терминов, которые делают возможной математическую модель.

* Ожидаемая доходность. Это процентная доходность, ожидаемая от инвестиций. Его можно рассчитать с помощью статистического анализа исторических тенденций.

* Стандартное отклонение. Определяет волатильность конкретного финансового актива. Это мера риска, связанного с инвестициями, то есть актив с высокой дисперсией несет в себе высокий риск и высокую прибыль. Он также оценивается с помощью статистического анализа тенденций данных.

* Ковариация. Оценивает взаимосвязь между различными объектами. Ковариация помогает оптимизировать распределение портфеля, изменяя веса активов в зависимости от ковариаций.

Давайте построим портфель по трем акциям: A, B и C. Инвестор стремится выяснить, сколько средств следует вложить в ту или иную акцию. Предположим, что для данных акций каждая акция обладает следующими характеристиками.

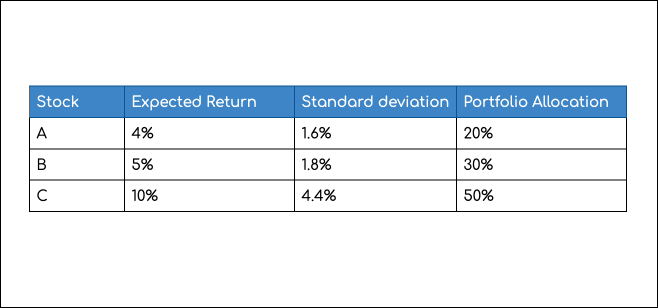n Если общая сумма инвестиций составляет 1000 долларов США, 200 долларов США для акции A, 300 долларов США для акции B и 500 долларов США для C. Учитывая распределение, средняя доходность портфеля составит .

Проценты распределения также считаются весами профиля, поскольку они определяют, сколько инвестиций идет в тот или иной актив.

Вторым важным фактором, который следует учитывать здесь, является дисперсия портфеля или риск. Портфельный риск сложнее рассчитать, поскольку он учитывает ковариацию различных активов. Оптимальный портфель по модели Марковица включает активы с отрицательной корреляцией. Если один актив упадет, другой вырастет и компенсирует его потерю, снижая общий риск портфеля.

Формула отклонения портфеля будет выглядеть так:

Ковариацию необходимо рассчитывать для каждой пары активов в портфеле. Предположим, наши активы имеют следующую матрицу корреляции.

Учитывая значения корреляции и приведенное выше стандартное отклонение, мы можем рассчитать ковариации, используя следующую формулу:

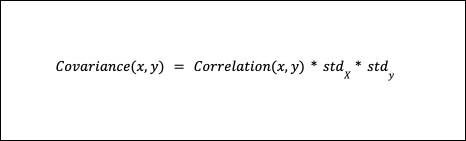
Ковариационная матрица становится

Используя рассчитанные выше значения, ковариация нашего портфеля становится

Граница эффективности

Приведенный выше пример демонстрирует одну из возможностей инвестиционного портфеля. Теория Марковица создает множество комбинаций таких портфелей с использованием разных значений распределения (весов). Различные портфели демонстрируют различные уровни доходности для данного значения риска (дисперсии). Эти различные портфели визуализируются на диаграмме под названием «Граница эффективности».

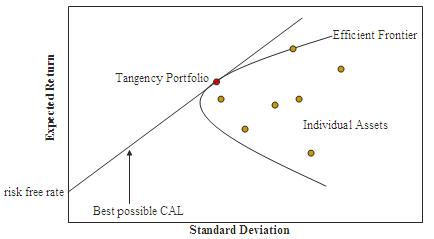
Кривая представляет собой компромисс между риском и прибылью, когда инвесторы заинтересованы во всем, что находится выше этой линии. Еще одним интересным фактором на этом графике является линия распределения капитала (CAL), которая проходит от безрисковой точки (нулевое стандартное отклонение) и образует касательную к кривой. Точка касания имеет самое высокое соотношение прибыли к риску и является лучшим портфелем для инвестиций.

Основные выводы

Инвестиционный портфель состоит из различных активов, таких как акции и облигации. Каждый инвестор начинает с основного инвестиционного капитала и решает, сколько инвестировать в каждый актив. Методы обработки данных, такие как теория средней дисперсии Марковица, помогают определить оптимальное распределение акций для создания оптимального портфеля.

Теория формулирует математическую модель для оптимизации распределения активов для получения максимальной прибыли при заданном уровне риска. Он анализирует различные финансовые активы и учитывает их доходность и факторы риска с учетом их исторических тенденций. Норма доходности — это приблизительное значение того, какую прибыль принесет актив за определенный период времени. Фактор риска определяется количественно с использованием стандартного отклонения стоимости актива. Более высокое отклонение представляет собой волатильный актив и, следовательно, более высокий риск.

Значения доходности и риска рассчитываются для различных комбинаций портфелей и представлены на кривой эффективной границы. Кривая помогает инвесторам определить максимальную прибыль от выбранного риска.