Ежедневная проблема кодирования: треугольные числа и большие делители
14 июля 2023 г.Добро пожаловать всем, у кого есть еще одна проблема! Сегодня поговорим о треугольных числах и их делителях: особенно о огромных!
Пока мы можем восхищаться моим потрясающим художественным представлением треугольных чисел в природе, давайте сделаем наши обычные оговорки:
- Эту задачу решает замечательный веб-сайт ProjectEuler.net, который вы можете подписаться здесь! Вам предстоит решить более 800 задач по математике и программированию, а также обширный архив дискуссий по ним. Это буквально идеальный инструмент, чтобы забыться и узнать что-то новое! Проверьте это и попробуйте решить свои проблемы тоже!
2. Я не эксперт-программист: просто парень, который любит писать о подобных вещах и любит делиться своими снимками. Я уверен, что это не будет оптимальным решением, поэтому, если у вас есть лучшее решение или какие-либо идеи о том, как его оптимизировать, мы будем более чем рады, если вы захотите поделиться!
Хватит говорить, давайте посмотрим, что может предложить сегодняшняя проблема:
Последовательность треугольных чисел создается путем сложения натуральных чисел. Таким образом, 7-е число треугольника будет 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. Первые десять терминов будут такими: 1,3,6,10,15,21,28,36,45,55,…
Перечислим множители первых семи треугольных чисел:

Мы видим, что 28 – первое треугольное число, имеющее более пяти делителей.
Каково значение первого треугольного числа, имеющего более пятисот делителей?
Задача довольно проста: нас просят понять, какое первое треугольное число имеет более 500 делителей. Прежде всего, давайте получше разберемся, что такое треугольное число и что такое делитель.
Треугольные числа
Треугольные числа – это особое подмножество чисел, состоящее из суммы всех натуральных чисел до определенного числа. Они называются треугольными, потому что их всегда можно расположить треугольником. Вот несколько примеров:
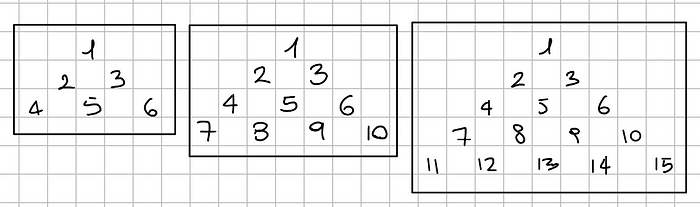
На изображении выше это 3-е, 4-е и 5-е треугольные числа. Так, например, 3-е число образуется как 1+2+3 = 6, 4-е как 1+2+3+4 = 10 и так далее. Вообще говоря, треугольное число nᵗʰ, Tₙ, равно
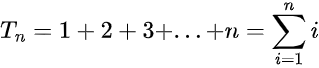
Это, конечно, один из самых известных математических рядов, представленный также Гауссом, который утверждал, что сумма последовательных целых чисел равна:
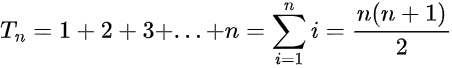
По сути, если мы хотим вычислить, например, третье треугольное число, мы просто вычисляем 3*4/2 = 6. Это будет очень полезно, когда мы начнем писать наше решение!
Разделители
Дать определение делителя (или множителя) числа n очень просто: это число j, которое можно умножить на другое целое число k, чтобы снова получить n. Например, 3 является делителем 18, потому что мы можем умножить 3 и 6, чтобы снова получить 18.
Однако 5 не является делителем 18, потому что не существует числа k, которое при умножении на 5 дает 18.
По определению мы также получаем важное свойство: если j является делителем n, потому что его можно умножить на k, чтобы получить n, тогда также k является делителем n, поскольку его можно умножить на j, чтобы получить n.
Таким образом мы можем быть уверены, что число n всегда имеет как минимум два делителя j и k (на самом деле , j всегда может быть равно 1, а k равно n).
Кроме того, другими словами, число j является делителем числа n, если остаток от n / j равно 0. Так, например, 18/3 = 6, а остаток равен 0.
Мы можем лучше формализовать эту концепцию с помощью модульной арифметики, говоря, что j является делителем n, если n % j = 0. Другими словами, мы получаем это второе свойство:
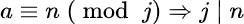
Третье и последнее свойство, которое нас интересует, заключается в том, что не может быть делителя числа n больше, чем n/2, а не n сам по себе. Это довольно просто понять. Из первого свойства мы знаем, что факторы каким-то образом «связаны» друг с другом в диапазоне 1,…,n.
Это потому, что опять же, если j n, это потому, что j * k = n. Следовательно, также k n. Давайте снова возьмем 18 в качестве примера. , найдите его делители и раскрасьте их, чтобы отразить это свойство.

Так, например, если j = 3, k = 6, и наоборот, если j = 6, k = 3, это означает, что наименьший j мы можем использовать, помимо 1, равно 2, что дает нам максимально возможное k, n/2 (9 в нашем случае)< em>. Это работает:
* для четных чисел, в этом случае наибольший множитель будет точно равен половине n;
* для нечетных чисел: если мы не можем разделить n на 2 (потому что нечетность даст нам рациональное число); это означает, что мы можем использовать только j > 2, который всегда будет давать нам результаты k < п/2.
Наконец, есть только один случай, когда j и k могут быть равны: когда n — квадратное число. Например, когда n = 36, возможный множитель j = 6 даст другой множитель k = 6. Мы будем обсудим этот случай подробнее позже в части кода.
Эти понятия, конечно, довольно тривиальны, но они будут очень важны в нашем решении!
Кодекс
Код будет написан на Go, так как это действительно быстрый язык, сохраняющий высокий уровень удобочитаемости. Мы разделим решение на две части: сначала мы создадим функцию для нахождения делителей числа, а затем применим ее к треугольным числам.
Давайте сначала посмотрим на функцию:
https://gist.github.com/NicolaM94/8fb97503da0c4d4431fcd5a858d13cdb?embedable=true Мы создаем нашу функцию, которая принимает целое число
Затем мы начинаем зацикливать
Таким образом, мы можем проверять наличие делителей только в первой половине
В каждом цикле мы проверяем 3 вещи:
* Второй оператор if проверяет, является ли
Предположим, что
* Первый оператор if является самым сложным: его цель — проверить, не появляются ли повторяющиеся пары j-k. Если это так, мы можем мгновенно разорвать цикл, потому что все наши факторы уже будут присутствовать в Что касается третьего пункта, необходимо проверить два случая:
Первый случай классический: возьмем, к примеру, число T₇ = 28: Когда
Второй случай возникает только тогда, когда мы нашли квадрат Когда
Наконец, мы можем просто Теперь, когда у нас есть функция, мы можем применить ее к каждому треугольному числу. Мы собираемся создать счетчик
Если их больше 500, мы возвращаем этот https://gist.github.com/NicolaM94/b01fb72874cb903982b887846fcc5c0c?em кровать = правда #file-main-go Но… есть одна загвоздка!
ProjectEuler.net — действительно прекрасный проект: помимо математических загадок и задач, их основной задачей является предоставление инструмента, с помощью которого можно начать учиться, думать и рассуждать о математике.
И мне это нравится: они настолько преданы делу, что публикация результатов и руководств по их задачам фактически запрещена (это одна из первых 100 задач, насколько я понимаю, она разрешена).
Учитывая это, я не думаю, что было бы справедливо просто раздать решение, чтобы скопировать-вставить и получить достижение. По этой причине я не даю вам фактического решения: попробуйте сами и попытайтесь придумать алгоритм лучше, чем мой (их много). Извините ребята! 😅 Я уверен, что есть много лучших решений, потому что мне кажется, что это довольно ужасный снимок! Функция
Однако сначала мы должны вычислить каждое треугольное число, что также занимает O(tn) времени, где tn — результат (последний, который мы фактически вычисляем). Учитывая это, примерно временная сложность всего алгоритма должна быть O(tn*n).
Поскольку
Я был удивлен, однако, что даже если алгоритм такой сложности, он, тем не менее, работает довольно быстро. Для выдачи результата на моей машине (AMD Ryzen 5, ср. ск. 2700 МГц) потребовалось 322,564227 мс.
Однако попытка найти первое треугольное число, превышающее 1000 делителей, заняла 3,827144472 секунды, поэтому ясно видно, что потребление времени быстро увеличивается. Наконец-то мы это сделали! Надеюсь, вам, ребята, понравилась статья, и я надеюсь, что вы могли бы извлечь из нее что-то интересное: если это так, пожалуйста, оставьте пару аплодисментов и поделитесь статьей с кем-то, кому может быть интересна эта тема!
Еще раз большое спасибо ProjectEuler за фантастическую работу: я действительно хочу предложить вам пойти и проверить, что они могут предложить; Уверен, вам будет очень интересно!
И, как всегда, спасибо за чтение.
Николаn и возвращает массив целых чисел out , который будет содержать наши делители. После этого мы добавляем к out тривиальные множители, а именно 1 и сам n.j от 2 до n/2 (со второго свойства; также обратите внимание, что сам n/2 нас не интересует потому что в случае, если n четное, k = n/2 будет добавлено к делителям на итерации j = 2: вот почему мы остановиться на j<n/2, а не на j≤ n/2). n , что немного ускоряет процесс.
n%j==0 , другими словами, если 0 ≡ n (mod j). Если да, то мы нашли фактор и добавляем j в список. Мы также можем добавить его аналог k в список, вычислив n/j и затем перейдя к следующему j ;n квадратом, и поэтому j является корнем n. Если да, то к out будет добавлен только один делитель j , чтобы избежать дублирования, а затем алгоритм продолжит работу. n = 36: если этот маленький блок будет отсутствовать, будет запущен третий оператор if, в результате чего out получит j = 6 и k = n/j = 36/6 = 6 , таким образом, создавая дубликат.out .out[len(out)-1] == j или out[len(out)-2] = = j .
j = 7 , оно будет равно последнему вставленному значению. Таким образом, мы можем разорвать цикл.n . Возьмем снова 36, например: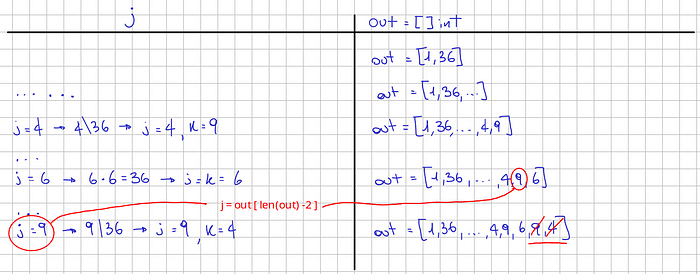
j = 9 , оно будет равно последнему значению, добавленному перед квадратным корнем из n , которое появляется только один раз. Следовательно, в этот момент мы можем разорвать цикл.вернуть значение, чтобы получить наши делители.Применение результатов
c, который будет служить генератором для наших треугольных чисел. Мы вычисляем соответствующее треугольное число tn с помощью уравнения Гаусса и проверяем, сколько у него делителей. tn в качестве результата.Временная сложность
FindDivisor выполняется за линейное время: поскольку оно зависит от размера экземпляра n , а также выполняется не более чем n/2 циклы; мы можем считать, что это O (n). tn становится аргументом или нашей функцией, и мы выполняем внутри него не более n/2 циклов, мы можем переписать временную сложность как O(tn*tn/2) = O(tn²/2) = O(tn²). Так что, к сожалению, квадратичное решение!Заключение
Оригинал