Преобразование отсортированного массива в двоичное дерево поиска

В большинстве случаев при написании кода для технического собеседования или просто для того, чтобы освежить в памяти структуры данных и amp; Навыки алгоритмов иногда забывают о двух важных аспектах: Качество кода и идиоматичности в языке программирования. используется.

Вот почему я решил написать этот пост.

В этом посте будут рассмотрены некоторые концепции Kotlin.

Понимание проблемы

В проблеме LeetCode говорится следующее,

Данный массив целых чисел nums, элементы которого отсортированы в порядке возрастания, преобразует его в сбалансированное по высоте[^1] двоичное дерево поиска.

Прежде чем мы начнем, несколько важных замечаний:

* nums уже отсортирован. * В качестве входных данных задается Массив. Таким образом, доступ к элементу будет операцией с постоянным временем O(1). * Длина nums не превышает 10^4, поэтому временная сложность должна быть хорошей. * Результирующее двоичное дерево поиска должно быть сбалансировано по высоте.

Это определение двоичного дерева в LeetCode:

class TreeNode(var `val`: Int) {
    var left: TreeNode? = null
    var right: TreeNode? = null
}

Алгоритм (рекурсивное решение)

Вот когда в игру вступает техника разделяй и властвуй.

Вот шаги, которые необходимо выполнить для создания BST:

1. Пусть n размер массива A и m = n/2 индекс среднего элемента, и выберите A[m] как корень BST[^2].
2. Рассмотрите два следующих смежных подмассива; A[… m-1] и A[m+1 …] соответственно, где A — массив с нулевым индексом, слева и справа вложенные смежные подмассивы.
3. Создайте левое и правое поддеревья с A[… m-1] и A[m+1 …] подмассивами, рекурсивно следуя шагу (1 ).
4. Повторяйте рекурсивно, пока не встретите пустой подмассив. Когда это произойдет, узел будет содержать значение null.

Следующая диаграмма иллюстрирует эту идею:

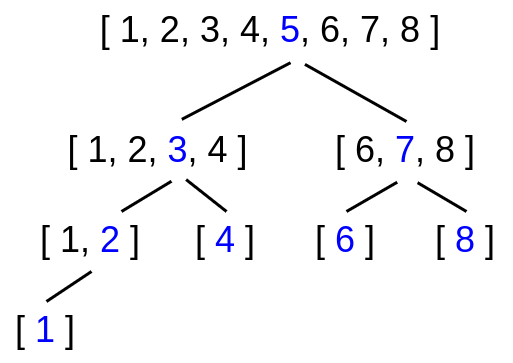
Реализация Котлина

class Solution {
    fun sortedArrayToBST(nums: IntArray): TreeNode? {
        fun makeTree(start: Int, end: Int): TreeNode? =
            if (start >= end) {
                null
            } else {
                val mid = start + (end - start) / 2

                TreeNode(nums[mid]).apply {
                    left = makeTree(start, mid)
                    right = makeTree(mid + 1, end)
                }
            }

        return makeTree(0, nums.size)
    }
}

Анализ кода

• Kotlin обеспечивает нулевую безопасность в системе типов. Вот почему используется тип TreeNode? вместо TreeNode. Во время компиляции мы можем узнать, допускает ли значение значение NULL или нет.

* Для построения дерева была создана локальная функция makeTree. Обратите внимание, что nums доступен внутри функции makeTree.

* start и end используются в качестве разделителей в бинарном поиске. Причина в том, чтобы избежать создания новых подмассивов.

* При выполнении бинарного поиска в пределах диапазона часто возникает ошибка, приводящая к целочисленному переполнению[^3].

Этот фрагмент вызовет переполнение

java val mid = (начало + конец) / 2

Во избежание переполнения индекс mid вычисляется как

java val mid = начало + (конец - начало) / 2

* В Kotlin if является выражением, оно возвращает значение . Воспользовавшись этим свойством, makeTree либо возвращает пустой узел (null), либо TreeNode. * Возвращает null, если нет допустимого диапазона для поиска в бинарном поиске. * Новый TreeNode, имеющий в качестве элемента значение mid, а левое и правое поддеревья строятся рекурсивно.

* Функция apply является функцией области действия. Используется для присвоения значений поддеревьям left и right. Это удобно при изменении свойств класса в стиле Kotlin.

<код>java TreeNode (числа [середина]). применить { слева = makeTree (начало, середина) справа = makeTree (середина + 1, конец)

Анализ сложности

• Временная сложность: O(n), где n обозначает размер массива.
• Пространственная сложность: O(h), где h обозначает высоту BST. Максимальная глубина рекурсии в стеке составляет h.

То есть BST строится за линейное время, и для этого требуется ч.

[^1]: сбалансированное по высоте бинарное дерево — это бинарное дерево, в котором глубина двух поддеревьев каждого узла никогда не отличается более чем на единицу.

[^2]: для простоты BST будет означать двоичное дерево поиска.

[^3]: Дополнительно, Дополнительно – Читать все Об этом: почти все бинарные поиски и сортировки слияния не работают