
Подготовка к собеседованию по программированию: алгоритмические головоломки и освоение поверхности куба
13 января 2024 г.В мире алгоритмов такие задачи, как вычисление площади трехмерной поверхности кубической сетки, не только интеллектуально стимулируют, но и оттачивают навыки решения проблем и логического мышления, необходимые в современной разработке программного обеспечения. Эта задача, взятая с веб-сайта HackerRank, представляет собой классическую алгоритмическую задачу, часто встречающуюся на собеседованиях по программированию. особенно с такими технологическими гигантами, как FAANG.
Проблема: сетка из кубов
Представьте себе сетку, в которой каждая ячейка может содержать стопку кубиков разной высоты, что очень похоже на миниатюрный городской пейзаж со зданиями разных размеров. Наша задача — вычислить общую видимую площадь поверхности этих сложенных друг на друга кубиков. Эта задача аналогична оценке видимого внешнего вида городского пейзажа, состоящего из зданий разной высоты.
Пример:
1 3 4
2 2 3 -> 60
1 2 4
Понимание расположения кубов и видимости поверхности

Каждый куб в нашей сетке похож на небольшое здание в городе. Задача состоит в том, чтобы выяснить, какие части этих зданий видны с внешней точки зрения.
- Верхняя и нижняя поверхности. Независимо от высоты куба, его верхняя и нижняя поверхности всегда видны, если они не закрыты другим кубом непосредственно сверху.
- Боковые поверхности. Видимость сторон куба зависит от его высоты относительно соседних кубов. Если куб выше своего соседа, видна часть, превышающая высоту соседа. Если он такой же высоты или короче, сторона будет скрыта.
Чтобы точнее оценить боковую видимость, мы рассматриваем каждый куб относительно его непосредственных соседей:
- Полностью видимая сторона. Если на какой-либо стороне нет соседнего куба, видна вся эта сторона.
- Частично видимая сторона. Если сосед куба короче, разница в высоте является видимой частью.
- Нет видимости. Если сосед такого же роста или выше, сторона куба не видна.
- Левый сосед (1,1) имеет высоту 2. Видимая боковая область = ==3 - 2 = 1==.
- Правый сосед (1,3) находится за пределами границ, предположим, что высота равна 0. ==3 - 0 = 3==
- Верхний сосед (0,2) имеет высоту 4. ==Нет видимой боковой области (=0)==, поскольку 3–4 отрицательны.
- Нижний сосед (2,2) имеет высоту 4. ==Нет видимой боковой области (=0)==, поскольку 3–4 отрицательно.
- S: представляет общую площадь поверхности, которую мы хотим рассчитать.
- ∑: этот символ обозначает суммирование. Это означает, что мы суммируем следующее выражение для каждого куба в сетке.
- i, j: это индексы, обозначающие положение каждого куба в сетке.
- 2: учитывает верхнюю и нижнюю поверхности каждого куба. Поскольку эти поверхности всегда видны для каждого куба, мы считаем две единицы площади для каждого куба.
- ∑ (di, dj) ∈ соседей: суммирование выполняется по каждому соседу куба. Соседи — это соседние кубики в сетке. Термины «di» и «dj» представляют относительное положение этих соседних кубов по отношению к текущему кубу, расположенному в точке (i, j).
- neighbours: эта переменная представляет список пар, где каждая пара (di,dj) определяет относительные позиции соседних кубов относительно текущего куба в точке (i,j). Например, (0,1) обозначает соседний куб, расположенный справа от текущего куба, а (1,0) представляет соседний куб, расположенный чуть ниже текущего куба. Список продолжает перечислять все соседние позиции, охватывая верхнее, нижнее, левое и правое направления, обеспечивая комплексную оценку соседних кубов для каждого куба в сетке.
- A[i][j]: это высота куба в позиции (i, j). Он показывает, сколько кубов сложено в этой конкретной позиции сетки.
- A[i+di][j+dj]: высота куба в соседней позиции. Это высота стопки кубиков в одной из ячеек, соседних с ячейкой (i, j).
- max(A[i][j] - A[i+di][j+dj], 0): эта часть формулы вычисляет площадь видимой стороны для каждой пары соседних кубики. Вычитаем высоту соседа (A[i+di][j+dj]) из высоты текущего куба (A[i][j]). Если результат положительный, это означает, что видна часть стороны текущего куба. Мы используем функцию max, чтобы гарантировать, что мы не учитываем отрицательные значения, которые подразумевают, что сторона не видна, поскольку соседний куб выше.
- Вычислительная геометрия и 3D-визуализация. Подобно вычислению видимых поверхностей куба, в этих полях используются алгоритмы для визуализации сложных форм и определения видимых областей.
- Компьютерная графика и виртуальная реальность. Алгоритмы оценивают видимость сложных форм, что похоже на проблему поверхности куба, что имеет решающее значение для реалистичной визуализации в играх и виртуальной реальности.
- Поиск пути в искусственном интеллекте и игровом дизайне. Такие алгоритмы, как A* и алгоритм Дейкстры, оценивают эффективные маршруты, что соответствует концепции видимости в задаче о кубе.
- Вычислительная геометрия ГИС: используется для анализа видимости, например линий обзора и видов горизонта, повторяя логику расчета поверхности куба.
Этот анализ предполагает тщательное рассмотрение положения каждого куба и его взаимосвязи с окружающими кубами, что позволяет нам точно суммировать все видимые области.
Это приводит к идее решения: каждая ячейка сетки посещает своих 4-х соседей, суммируя все разницы высот.
Чтобы проиллюстрировать эту концепцию, давайте углубимся в приведенный пример и разберем шаг за шагом расчет площади поверхности:
1 3 4
2 2 3
1 2 4
Первоначально мы создаем новую матрицу, отражающую размеры нашей сетки. Эта матрица будет постепенно заполняться рассчитанной площадью поверхности каждого отдельного куба. Для каждого куба, если его высота больше нуля, он добавляет две единицы площади (для верхней и нижней поверхностей). Мы добавляем их в нашу матрицу площади поверхности.
2 2 2
2 2 2
2 2 2
Вычисление боковых поверхностей. Теперь мы исследуем стороны каждого куба. Сторона видна, если куб выше соседнего куба. Видимая площадь – это разница их высот. Мы делаем это для каждого куба, сравнивая его с соседями (слева, справа, сверху и снизу).
Например, для куба (1,2) высотой 3:
1 3 4
2 2 3 <- this one
1 2 4
Итак, общая площадь поверхности этой стопки кубиков составит:
2(уже записано в матрице) + 1(слева) + 3(справа) + 0 + 0 = ==6==.
Итак, давайте обновим наше значение:
2 2 2
2 2 6 <- here it is
2 2 2
Мы выполняем аналогичные вычисления для каждого куба и обновляем нашу матрицу.
Подведение итогов. После расчета площадей всех кубов мы суммируем значения в нашей матрице площадей поверхностей. Эта сумма дает нам общую видимую площадь поверхности всей сетки кубов.
После выполнения этих шагов мы получаем матрицу, которая представляет площадь поверхности каждого куба, и суммируя все эти значения, мы получаем общую видимую площадь поверхности сетки.
4 8 12
6 2 6
4 5 13
После суммирования этой матрицы площадей мы получаем окончательный ответ 60. Этот методический подход помогает визуализировать и понять проблему, что упрощает ее реализацию в контексте программирования.
Математическая формулировка
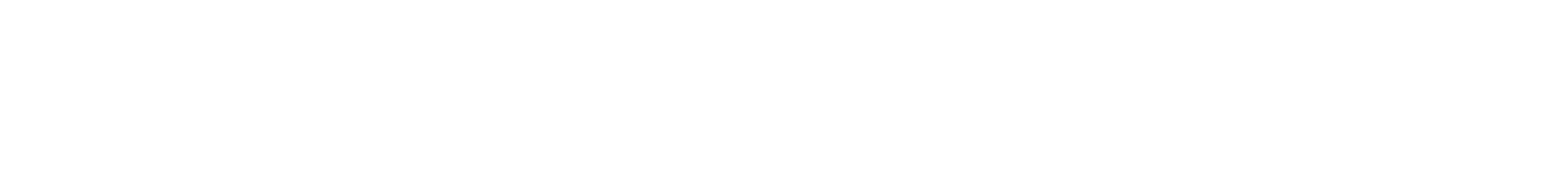
Теперь давайте углубимся в саму формулу и разберем ее компоненты:
Реализация
Пример реализации, которая, по сути, просто реализует нашу производную формулу в Python, можно найти ниже. Он также суммирует всю площадь непосредственно в результирующую переменную, а не в промежуточную матрицу, поскольку нам нужна только общая площадь.
NEIGHBOURS = [
(0, 1),
(1, 0),
(-1, 0),
(0, -1)
]
# helper function
def height(A, i, j):
n = len(A)
m = len(A[0])
if 0 <= i < n and 0 <= j < m:
return A[i][j]
return 0
def surfaceArea(A):
n = len(A)
m = len(A[0])
area = 0
for i in range(n):
for j in range(m): # outer sum by all the grid
if height(A, i, j) > 0:
area += 2
for (di, dj) in NEIGHBOURS: # inner sum by neighbours
neighbour_h = height(A, i + di, j + dj)
diff_height = height(A, i, j) - neighbour_h
area += max(diff_height, 0)
return area
Похожие реальные проблемы и области
Понравилось глубокое погружение в алгоритмическое решение задач? Оставайтесь с нами, чтобы увидеть больше интригующего контента!
Оригинал

