
Аспекты термической феноменологии КХД при соединении промежуточного калибра и копыта: Приложение C
26 февраля 2024 г.:::информация Авторы:
(1) Гопал Ядав, физический факультет Индийского технологического института; Ченнайский математический институт.
:::
Таблица ссылок
ЧАСТЬ I
Глава 2: SU(3) LEC из теории струн типа IIA
Глава 4: Заключение и перспективы на будущее
ЧАСТЬ II
Глава 6: Кривые страницы черной дыры Рейсснера-Нордстрема в HD-гравитации
Глава 8: Острова черных дыр в многособытийном горизонте пространства-времени
Глава 9: Мультивселенная в мире бран Карча-Рэндалла
Глава 10: Заключение и перспективы на будущее
ПРИЛОЖЕНИЕ C
C.1 Комплексные внешние кривизны и тензоры Римана

Мы можем перейти от комплексных тензоров Римана к действительным тензорам Римана, используя следующие преобразования координат:
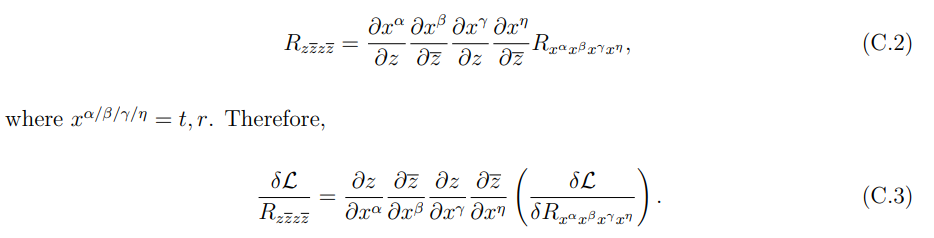
Аналогично, для вычисления второго члена формулы энтропии голографической запутанности мы используем следующие преобразования координат:
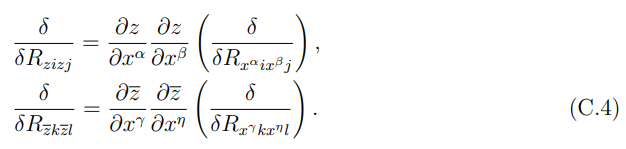
Следовательно, используя уравнение (C.4), мы можем получить второй член, появляющийся в формуле энтропии голографической запутанности, в терминах действительных координат (t, x), используя преобразования координат, приведенные ниже:
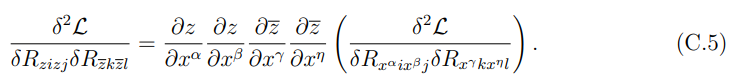
C.2 HM-подобный/IS-аналитика/числовые данные
В настоящем приложении мы описываем (i) угловое интегрирование, используемое в ходе вычислений, и уравнение, описывающее площадь поверхности, подобной Хартману-Малдасене, и (ii) процесс, с помощью которого мы оцениваем точку поворота в контекст энтропии запутанности поверхности острова.
C.2.1 Площадь поверхности, подобная HM

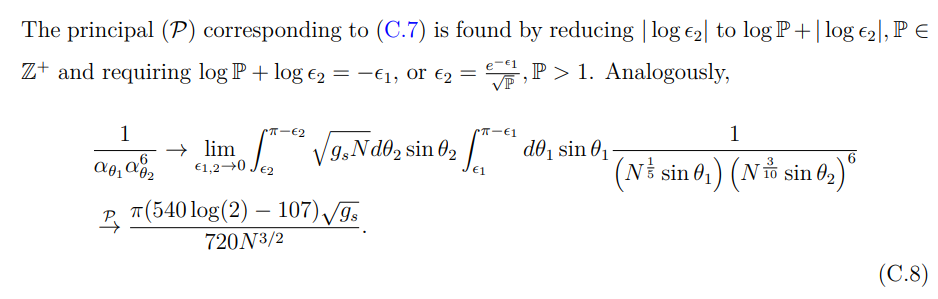

C.2.2 Поворотный момент


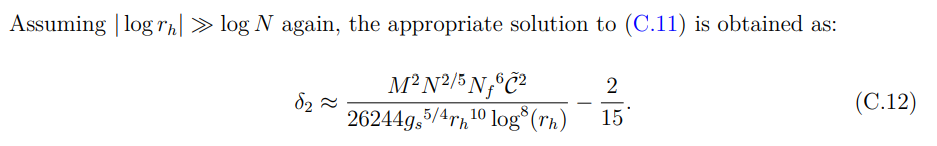
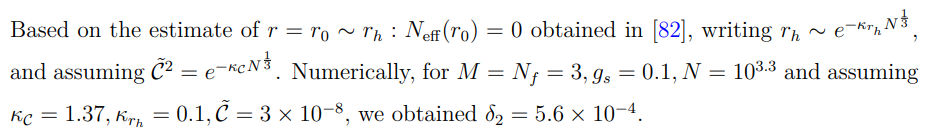
C.3 Поверхностная смесь типа Хартмана-Мальдасены
В этом приложении мы представляем многочисленные r-зависимые функции, которые появляются в формуле энтропии запутанности для описания поверхности типа Хартмана-Малдасены в точках O(β 0 ) и O(β). Мы также рассчитали уравнение движения, относящееся к функции вложения, связанной с поверхностью типа Хартмана-Малдасены.
• Зависимые от r функции, входящие в уравнение (7.57), имеют вид:
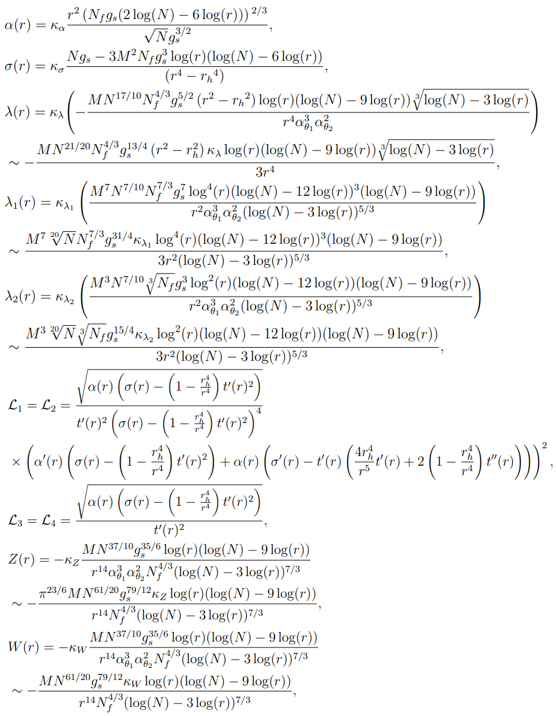

• В случае существования членов с более высокой производной для вычисления первого и второго членов при вычислении энтропии голографической запутанности использовалось следующее:
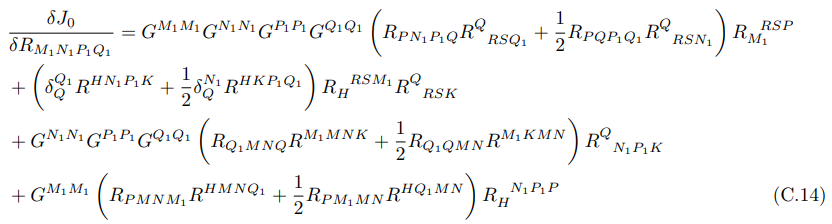
и
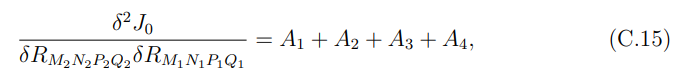
где
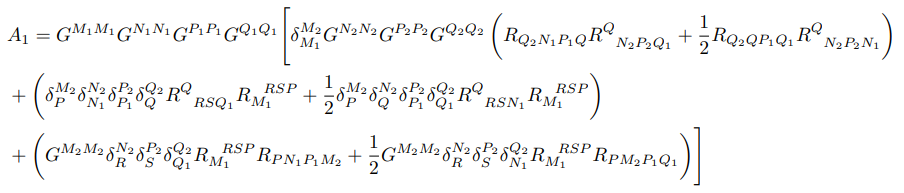
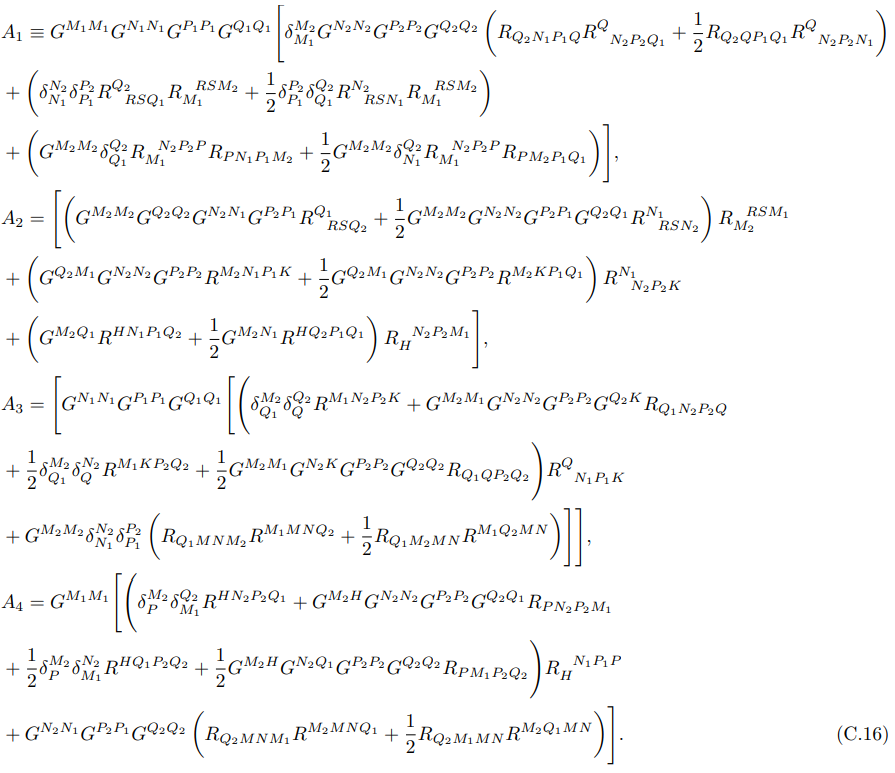
• Чтобы вывести уравнение движения, связанное с вложением t(r), мы должны вычислить производные, полученные из уравнения (7.56):
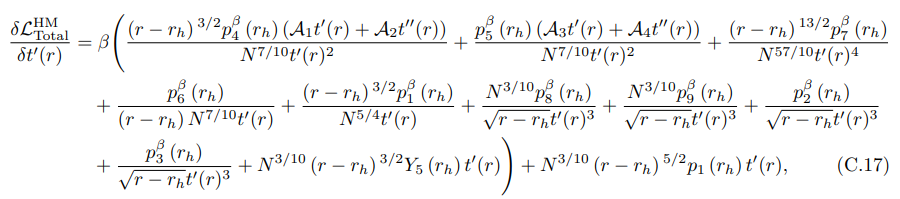
и

где
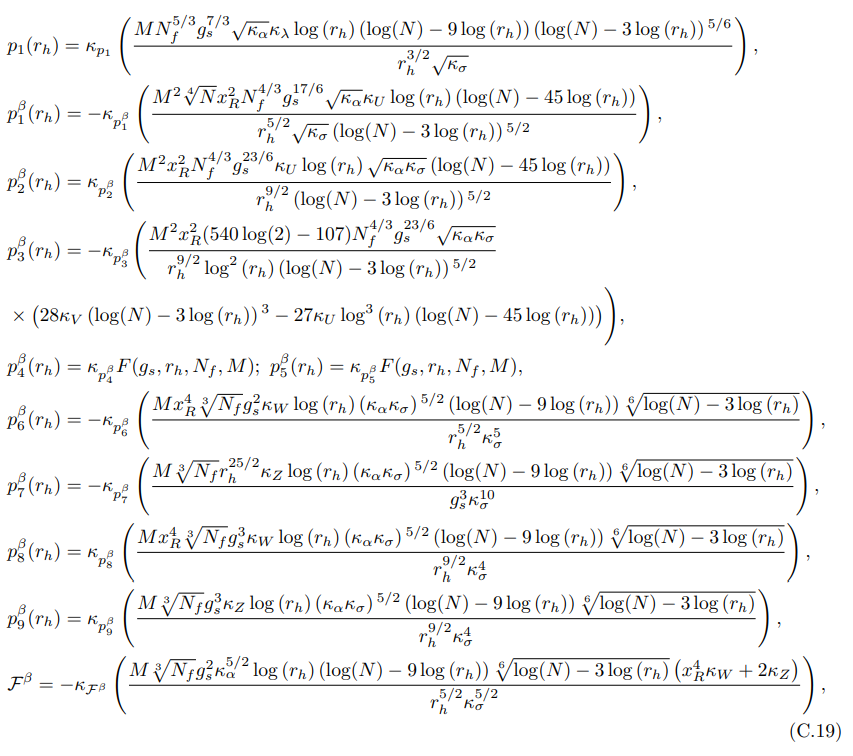

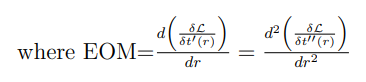
C.4 Разное на поверхности острова
В этом приложении мы перечисляем множество функций, которые возникают из энтропии запутанности поверхности острова в точке O(β). Здесь мы дополнительно рассчитали производные лагранжиана, связанные с поверхностью острова, которые были использованы для расчета уравнения движения, касающегося встраивания поверхности острова.
• Следующие члены (λ3,4(r)) существуют в члене энтропии перепутывания Вальда (первый член голографической энтропии перепутывания (7.78)) поверхности острова:
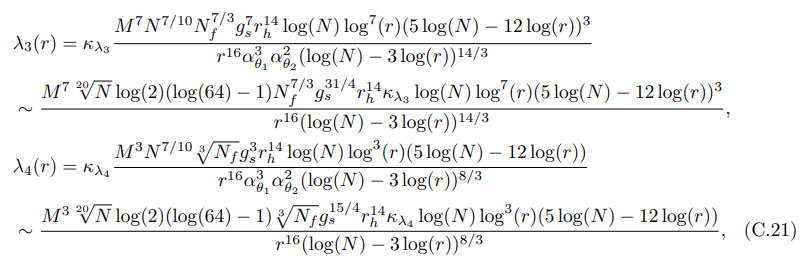
где κλ3 и κλ4 — числовые коэффициенты.
• Зависимые от r функции появляются в аномальном члене (втором члене энтропии голографической запутанности (7.78)) следующие:
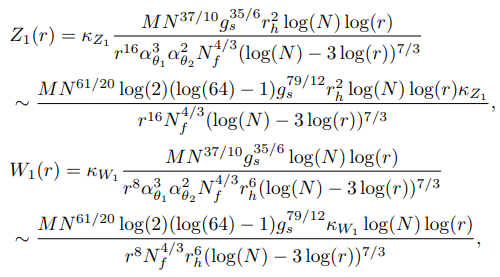

• Для действия, связанного с вложением поверхности острова (7.79), мы получили:
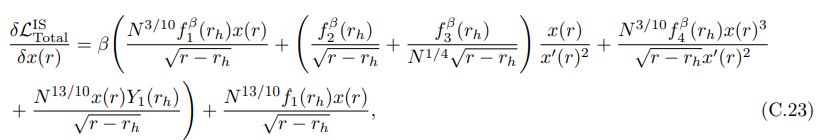
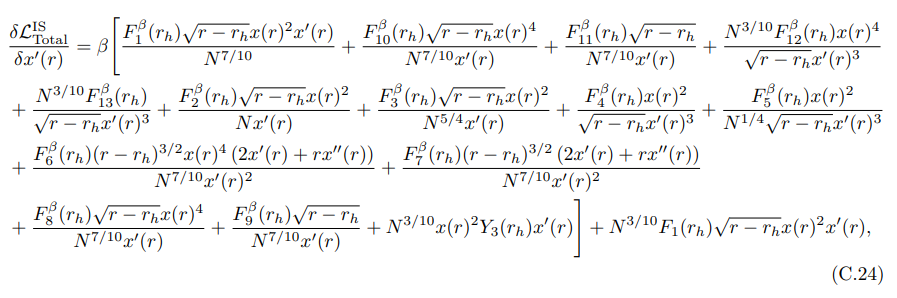
и
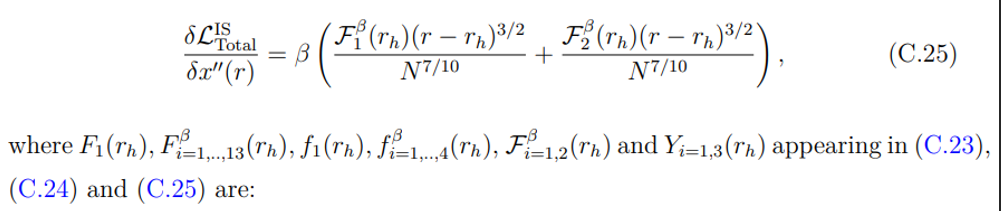

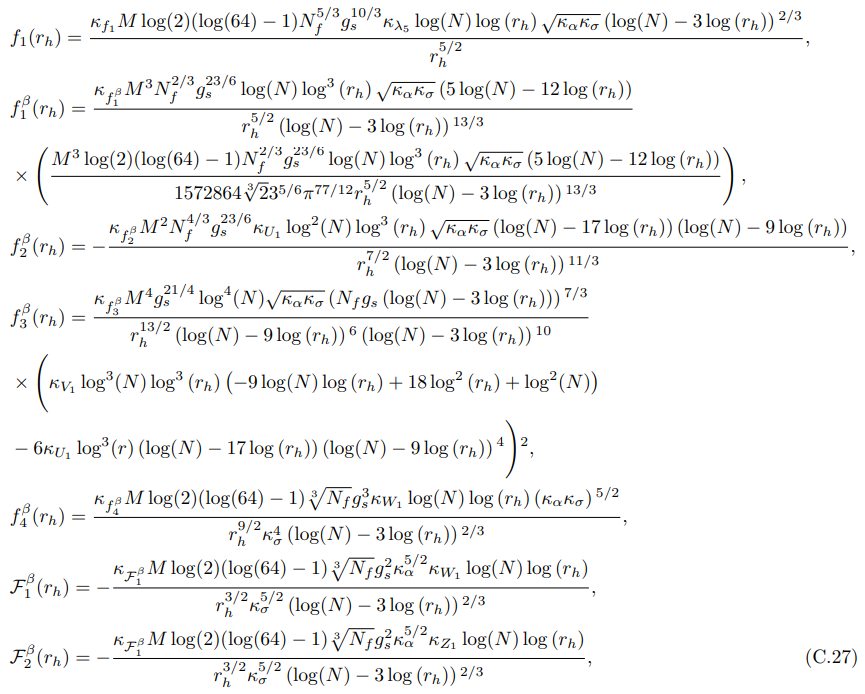
и
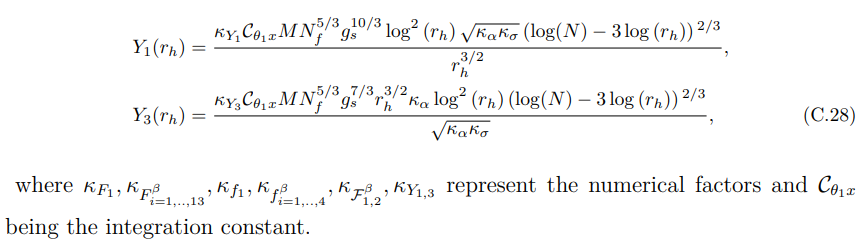
C.5 Возможные члены, возникающие в энтропии голографической запутанности
В этом приложении мы предоставили все члены, которые можно было получить путем дифференцирования лагранжиана двойственной М-теории, включая поправки O(R4). Мы включили все слова, связанные с поверхностью типа Хартмана-Малдасены, в C.5.1, а все доступные термины, связанные с поверхностью острова, в C.5.2.
C.5.1 Поверхность типа Хартмана-Малдасены
• √ -g Связано с индуцированной метрикой (7.23):
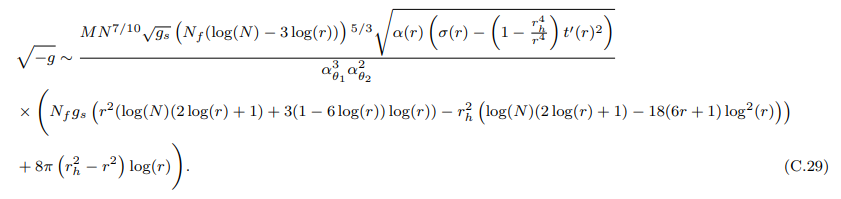
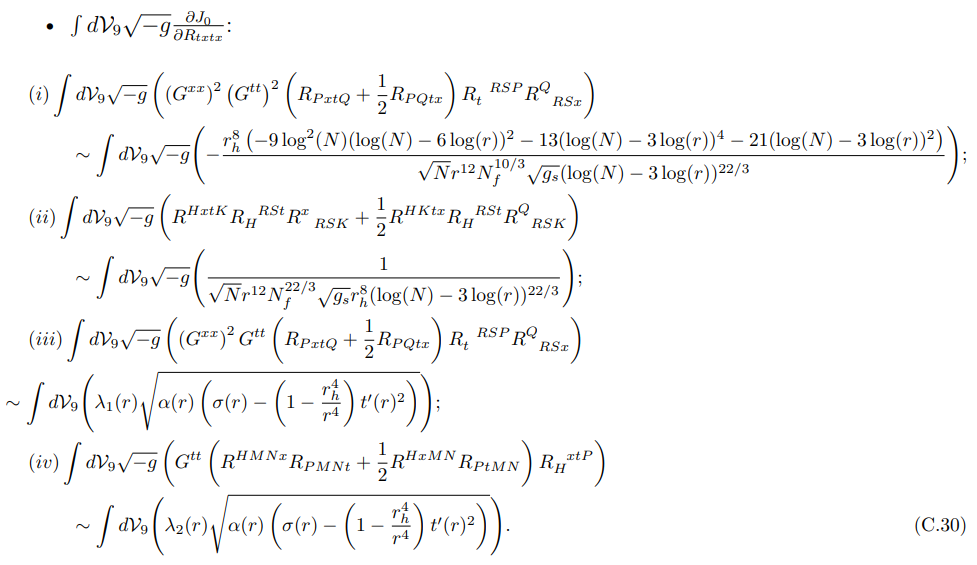
Уравнение (C.30) предполагает, что в пределе большого N члены (iii) и (iv) соответствуют наиболее доминирующим членам.

где нет зависимости от N в G1(r) и G2(r). Термины (v) и (xii) являются наиболее заметными в пределе большого N среди всех терминов, указанных выше.

где G3(r) и G4(r) не зависят от N. Условия (v) и (xii) являются наиболее доминирующими в пределе большого N.
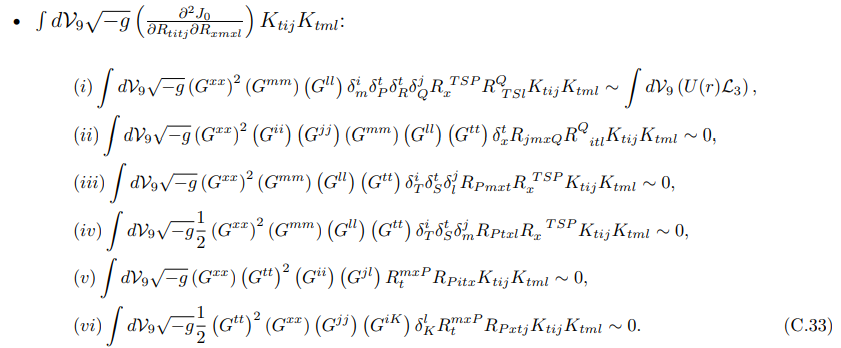
Поскольку только первый член ненулевой, и, следовательно, это вносит вклад в лагранжиан.
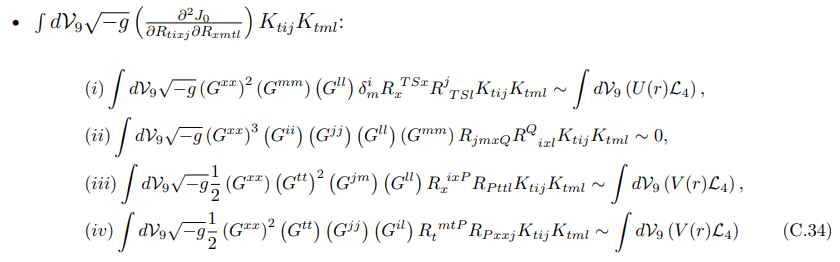
Для приведенного выше уравнения мы обнаружили, что все три ненулевых члена масштабируются как N, и, следовательно, мы сохранили все ненулевые члены в лагранжиане.
C.5.2 Поверхность острова
• √ -g Связано с индуцированной метрикой (7.40):
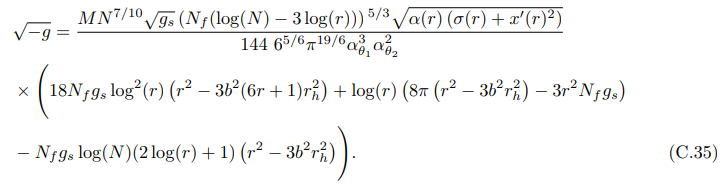
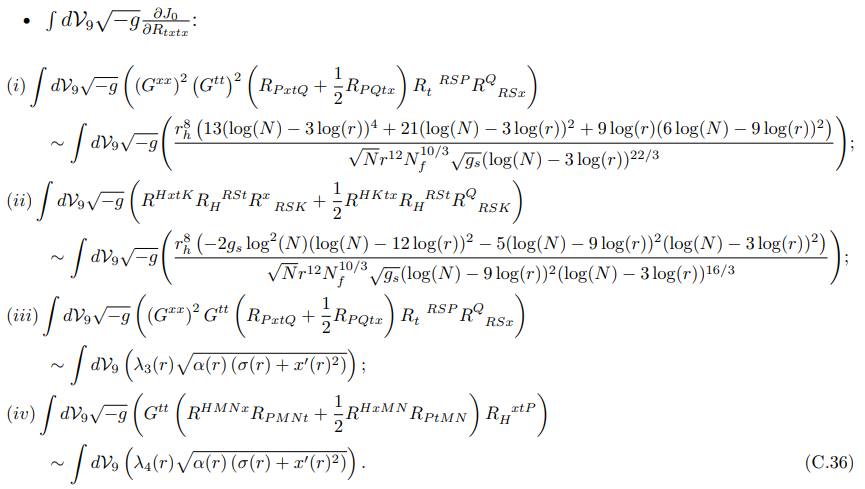
В пределе большого N члены (iii) и (iv) оказываются наиболее доминирующими.

где G5(r) и G6(r) не зависят от N. Мы обнаружили, что члены (v) и (xii) доминируют по сравнению с другими членами в пределе больших N.

где G7(r) и G8(r) не зависят от N, а наиболее доминирующими членами являются (v) и (xii) в пределе больших N.


:::информация Этот документ доступен на arxiv по лицензии CC 4.0.
:::
Оригинал

