blockchain hackernoon-top-story blockchain-technology algorithms blockchain-writing-contest cryptography tatum_io shamir-secret

Введение в криптографический алгоритм обмена секретами Шамира

24 мая 2022 г.

Обмен секретами Ади Шамира — это криптографический алгоритм, который позволяет разным сторонам совместно владеть одним секретом, владея долями. Первоначальный секрет можно восстановить только с использованием минимального количества акций, что позволяет различным сторонам сотрудничать без необходимости полностью доверять друг другу.

Пример проблемы

Для иллюстрации давайте представим, что семья из четырех человек пользуется одним биткойн-кошельком. Этот биткойн-кошелек содержит единственный закрытый ключ, которым совместно владеют все члены семьи. Поскольку существует единственный ключ, любой из членов семьи может использовать этот ключ, чтобы потратить все биткойны.

У семьи есть проблема: если у каждого из них есть копия, то только одна из их копий должна быть скомпрометирована, чтобы украсть все монеты. Если только один из них хранит ключ, то этот человек может его потерять или решить обмануть других членов семьи.

К счастью, один из членов семьи также является криптографом. Вместо того, чтобы наивно делиться исходным ключом, они используют SSS (обмен секретами Шамира). Семья создает четыре доли и устанавливает порог в три, используя биткойн-ключ в качестве исходного секрета. Теперь их план имеет следующие свойства:

Они не хранят биткойн-ключ в одном месте, что затрудняет его кражу.

Члены семьи должны сотрудничать, чтобы тратить биткойны, один член семьи не может предать других

Если член семьи умирает или теряет свою долю, остальные три члена могут восстановить ключ

Понимание порога

Каждая схема обмена Shamir имеет общее количество акций и пороговое значение. Порог — это количество долей, необходимое для восстановления исходного секрета. Например, с пятью долями и порогом в три вам нужны только три из пяти долей для вычисления исходного секрета.

Математика — Линии

Одним из фундаментальных математических свойств, использованных при обмене секретами Шамира, является тот факт, что для определения многочлена степени k - 1 требуется k точек. Например:

Между двумя точками можно провести только одну линию

Только одна возможная парабола проходит через одни и те же три точки

Только одна кубическая кривая проходит через одни и те же четыре точки

Через одну и ту же точку можно провести бесконечное количество линий

Через одни и те же две точки можно провести бесконечное количество парабол

Математика - Прохождение

Давайте создадим схему, чтобы поделиться нашим секретом 1954 (S) с 4 (n) долями и порогом 3 (k).

Во-первых, мы случайным образом выбираем k - 1 положительное целое число, то есть в нашем случае 2 положительных целых числа. Мы случайным образом выбираем 43 и 12.

Затем строим многочлен вида

у = а0 + а1х + а2х^2

Где a0 — это секрет, а a1 и a2 — наши случайно выбранные целые числа. Нам остается:

у = 1954 + 43x + 12x^2

Затем мы используем эту формулу для создания 4 баллов (долей), которые мы даем каждому участнику.

Поделиться 1

(х, у), где х = 1

у = 1954 + 43*1 + 12*1^2 = 2009

(1, 2009 г.)

Поделиться 2

(х, у), где х = 2

у = 1954 + 43*2 + 12*2^2 = 2088

(2, 2088)

Поделиться 3

(х, у), где х = 3

у = 1954 + 43*3 + 12*3^2 = 2191

(3, 2191)

Поделиться 4

(х, у), где х = 4

у = 1954 + 43*4 + 12*4^2 = 2318

(4, 2318)

Реконструкция

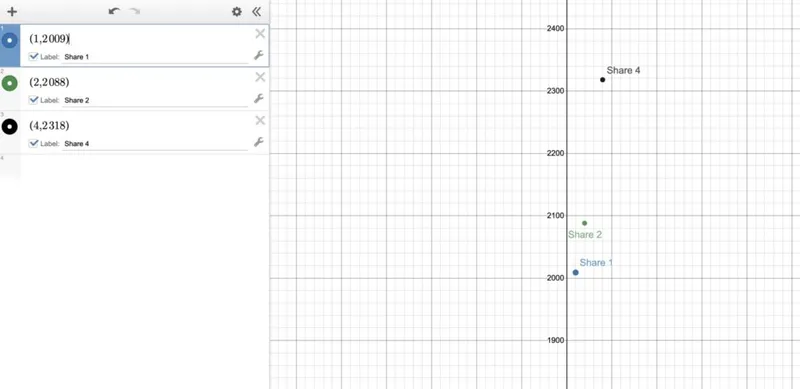
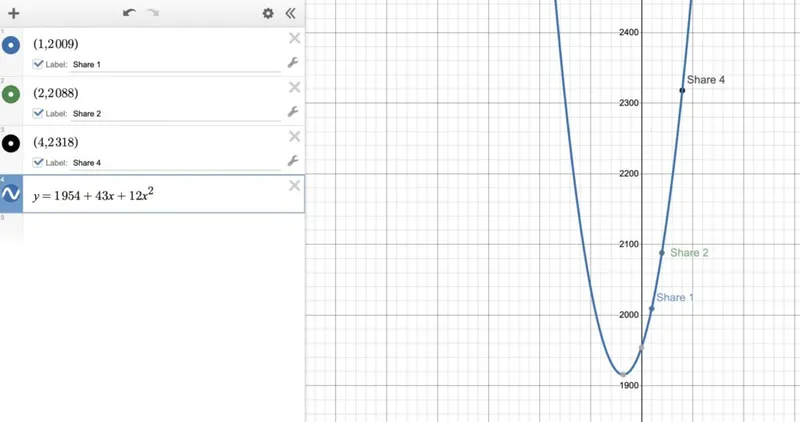
Каждый участник нашей схемы теперь владеет одним (x,y) пунктом, который представляет собой одну акцию. Помните, что мы установили наш порог равным 3 и что 3 точки идеально определяют параболу (многочлен степени 2). Это означает, что если мы используем три точки, мы можем нарисовать параболу и вычислить a0 (секрет). Предположим, у нас есть контроль над акциями 1, 2 и 4.

Шаг 1 - Нанесите точки (акции), которые мы контролируем

Шаг 2 - Нарисуйте соответствующую параболу

Шаг 3 - Найдите точку, где `x=0`. Его значение y является секретом

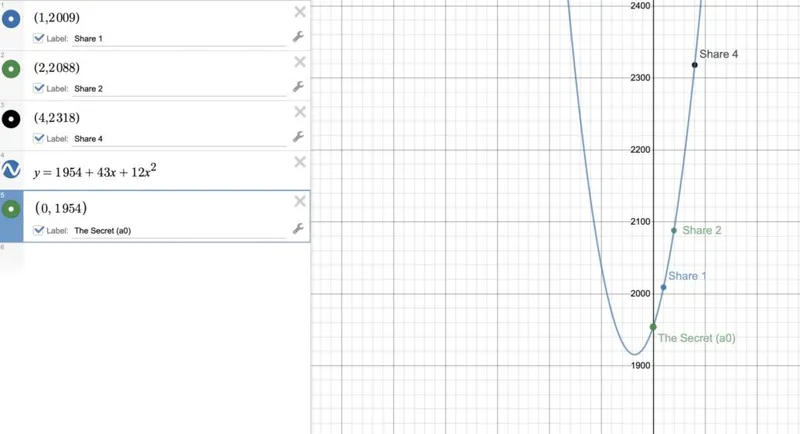
В нашем случае секрет 1954.

На самом деле все не так просто. Нам нужны конечные поля.

Хотя пример, который мы рассмотрели выше, отлично подходит для демонстрационных целей, на самом деле он не очень безопасен. С каждой долей, которую получает злоумышленник, он фактически получает все больше и больше информации о секрете. Хотя две точки не полностью описывают параболу, они все же дают критическую информацию о параболе.

Решение лежит в арифметике конечного поля. При построении функции на конечном поле достаточного размера график полинома становится непересекающимся и разбросанным, что означает, что злоумышленник не может делать обоснованные предположения о пути базовой функции.

Ади Шамир

Ади Шамир — израильский криптограф, известный благодаря своей книге Shamir's Secret Sharing, но он также является соавтором широко используемого алгоритма RSA, на котором построено подавляющее большинство Интернета. Шамир родился в Тель-Авиве и получил степень бакалавра по математике в университете. Позже он получил степень магистра и доктора философии. получил степень в области компьютерных наук в Институте Вейцмана в 1975 и 1977 годах соответственно.

Оригинал

Введение в криптографический алгоритм обмена секретами Шамира

Пример проблемы

Понимание порога

Математика — Линии