Алгоритмическое проектирование контрактов: что нужно знать об агентах с неизвестными недостатками

:::информация Этот документ доступен на arxiv под лицензией CC 4.0.

Авторы:

(1) Кириаки Франгиас;

(2) Эндрю Лин;

(3) Эллен Витерчик;

(4) Манолис Зампетакис.

:::

Таблица ссылок

Аннотация и введение

Разминка: агенты с известной одинаковой бесполезностью

Агенты с неизвестными недостатками

Эксперименты

Выводы и будущие направления, Ссылки

Сводка обозначений

B Пропущенные доказательства из раздела 2

C Пропущенные доказательства из раздела 3

D Дополнительная информация об экспериментах

3 агента с неизвестными недостатками

Теперь мы значительно расширили нашу модель для изучения гетерогенных агентов с разными, неизвестными бесполезностями. Полные доказательства всех результатов этого раздела находятся в Приложении C.

3.1 Модель и обозначения

Некоторые агенты могут испытывать большую бесполезность при приложении усилий, поэтому стимулирование всех агентов к приложению усилий может быть не в интересах принципала. Следовательно, принципал должен установить оплату таким образом, чтобы количество стимулируемых агентов максимизировало полезность для принципала. В оставшейся части этого раздела мы обозначаем g количество агентов, которых принципал стремится стимулировать; в теореме 3.6 мы описываем эффективную задачу оптимизации, которая решается для оптимального значения g, обозначаемого g∗. Принципал контролирует количество мотивированных агентов только через платежную функцию. Следовательно, реализованное количество агентов, прилагающих усилия, обозначаемое ˆg, является случайной величиной, распределение которой зависит от оплаты. В соответствии с этой моделью директор будет:

1. Рассчитайте g∗ — оптимальное количество агентов для стимулирования.

2. Объявить выплату pg∗ ∈ R+ (на основе g∗).

3. Проверьте подмножество сравнений, назначенных агентам.

4. Присвойте каждому сравнению r агентов.

5. Выплатить pg* всем агентам, которые не определены как «плохие».

3.2 Функция оплаты

3.3 Корректность CrowdSort

Затем мы ограничили избыточность, необходимую для того, чтобы CrowdSort возвращал достоверный порядок.

Доказательство. Из леммы 3.4 мы знаем, что если

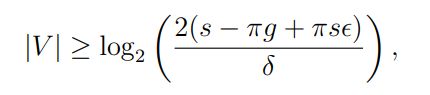
тогда с высокой вероятностью алгоритм CrowdSort(T, s, v, r, δ) идентифицирует всех «плохих» агентов. Следовательно, достаточно присвоить каждое сравнение хотя бы одному «хорошему» агенту, чтобы вернуть истинное значение сравнения. По замечанию 3.3 мы знаем, что для любого агента ai

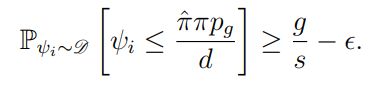
Таким образом, вероятность того, что все агенты r, назначенные для одного сравнения, являются «плохими», не превышает:

Принимая объединение всех сравнений, мы получаем, что вероятность существования такого сравнения, что все агенты, назначенные ему, являются «плохими», не превышает

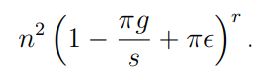
Ограничивая указанную выше вероятность сверху величиной δ/2, получаем следующее:

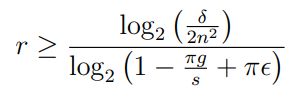
Наконец, заметим, что приведенное выше неравенство и неравенство (6) выполняются одновременно с вероятностью не менее 1 − δ/2.

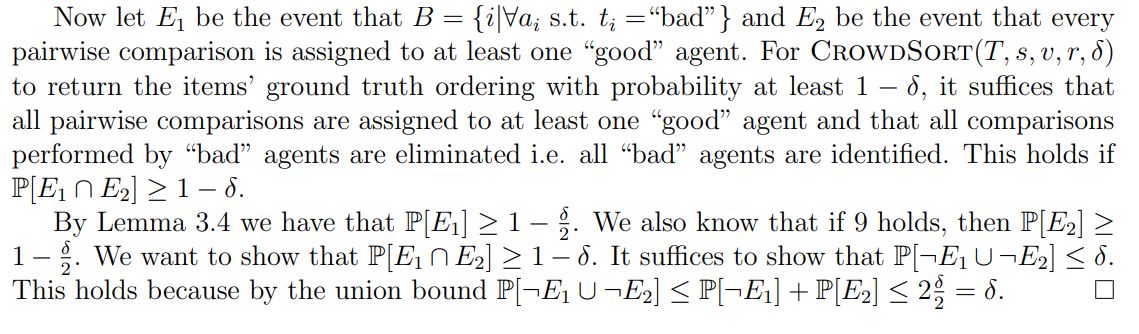
3.4 Поощрение директора

Мы объединяем результаты, представленные выше, в следующей теореме, в которой дополнительно доказываем, что принципал может эффективно вычислить оптимальное количество агентов для стимулирования. На основании леммы 3.5 воспользуемся обозначением

и

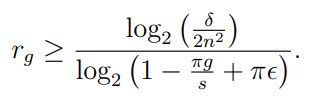
Этот документ доступен на Arxiv в разделе Лицензия CC 4.0.