Передовые методы разработки признаков данных временных рядов

Введение

Данные временных рядов являются ключевым компонентом в самых разных областях, включая финансы и метеорологию. Эффективная разработка признаков имеет решающее значение при подготовке данных временных рядов для моделей машинного обучения.

В этой статье мы углубимся в передовые методы разработки признаков временных рядов, такие как преобразование Фурье, вейвлет-преобразование, производные и автокорреляция.

Эти методы помогают обнаруживать скрытые структуры и тенденции, собирать информацию о времени и частоте, а также измерять линейную зависимость между точками данных при различных задержках.

Методы

Преобразование Фурье

Преобразование Фурье – это математический метод, который разлагает сигнал временного ряда на его частотные составляющие. Он основан на том принципе, что любой сигнал можно разбить на серию синусоидальных волн с различной амплитудой, частотой и фазой.

Фиксируя периодические закономерности в данных, преобразование Фурье может помочь выявить скрытые структуры и тенденции, которые могут быть полезны для прогнозирования.

Преобразование Фурье можно разделить на два типа: непрерывное преобразование Фурье (CFT) для непрерывных сигналов и дискретное преобразование Фурье (DFT) для дискретных сигналов.

Быстрое преобразование Фурье (БПФ) — это эффективный алгоритм вычисления ДПФ последовательности.

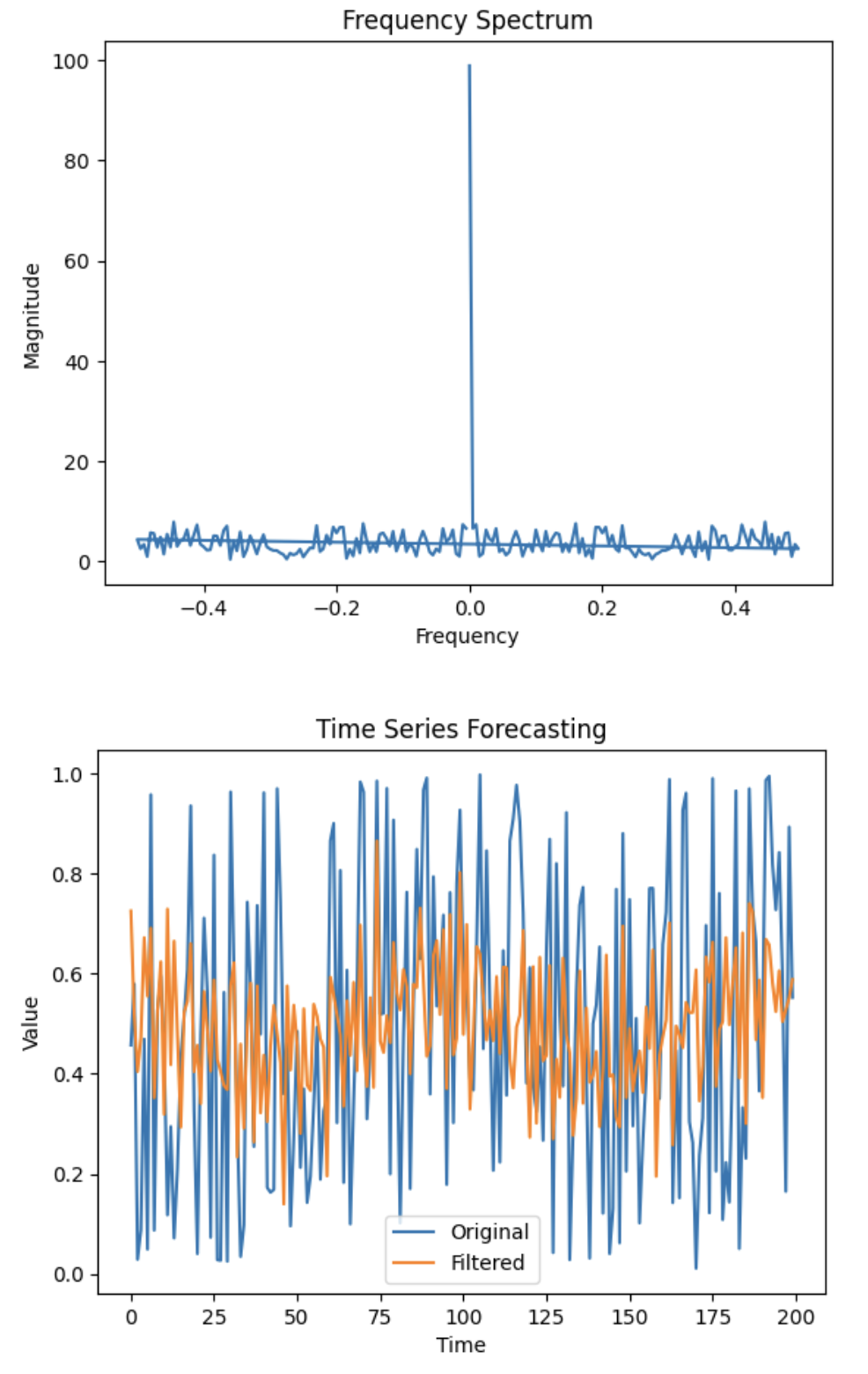
Спектральная плотность мощности, полученная из квадратов величин преобразования Фурье, может использоваться в качестве функции в моделях машинного обучения для повышения их производительности. Вот простой пример использования для БПФ:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.fft import fft, ifft


time_series = np.random.random(200)

# Perform Fast Fourier Transform (FFT)
fft_values = fft(time_series)

# Get the magnitude and frequencies
fft_magnitude = np.abs(fft_values)
frequencies = np.fft.fftfreq(len(time_series))

# Plot the frequency spectrum
plt.plot(frequencies, fft_magnitude)
plt.xlabel('Frequency')
plt.ylabel('Magnitude')
plt.title('Frequency Spectrum')
plt.show()

# Filter out the low magnitude frequencies
threshold = 7
fft_values_filtered = fft_values.copy()
fft_values_filtered[fft_magnitude < threshold] = 0

# Perform the inverse Fast Fourier Transform (IFFT)
filtered_time_series = ifft(fft_values_filtered)

# Plot the original and filtered time series
plt.plot(time_series, label='Original')
plt.plot(filtered_time_series.real, label='Filtered')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Time Series Forecasting')
plt.legend()
plt.show()

Вейвлет-преобразование

Вейвлет-преобразование – это математический метод, используемый для разложения сигнала на различные частотные компоненты. Это особенно полезно при анализе временных рядов, поскольку позволяет нам фиксировать в данных информацию как о времени, так и о частоте.

В отличие от разложения Фурье, в котором всегда используются сложные экспоненциальные (синусоидальные и косинусоидальные) базисные функции, вейвлетное разложение использует локализованную во времени колебательную функцию в качестве анализирующего или исходного вейвлета.

Наиболее распространенным вейвлет-преобразованием является непрерывное вейвлет-преобразование (CWT).

CWT определяется как:

Функция вейвлета может быть выбрана в зависимости от типа данных и желаемых функций. Популярным выбором является вейвлет Морле, произведение комплексной экспоненциальной функции и функции Гаусса, определяемой как:

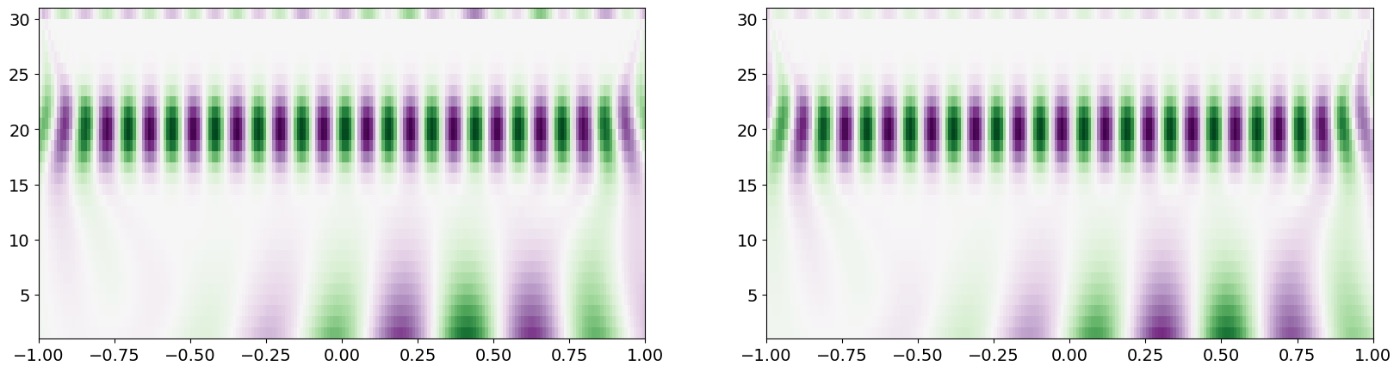
Пример Scipy для вычисления CWT с использованием вейвлета Морле:

from scipy import signal
import matplotlib.pyplot as plt

t = np.linspace(-1, 1, 200, endpoint=False)
sig = np.cos(2 * np.pi * 7 * t) + signal.gausspulse(t - 0.4, fc=2)
widths = np.arange(1, 31)

cwtmatr = signal.cwt(sig, signal.morlet2, widths)

real, imag = np.real(cwtmatr), np.imag(cwtmatr)

fig, axes = plt.subplots(ncols=2, figsize=(20, 5))
axes[0].imshow(
    real,
    extent=[-1, 1, 1, 31],
    cmap="PRGn",
    aspect="auto",
    vmax=abs(real).max(),
    vmin=-abs(real).max(),
)
axes[1].imshow(
    imag,
    extent=[-1, 1, 1, 31],
    cmap="PRGn",
    aspect="auto",
    vmax=abs(imag).max(),
    vmin=-abs(imag).max(),
)

Производные

Производные можно использовать для описания скорости изменения данных временных рядов. Например, первая производная представляет собой скорость, а вторая производная — ускорение. Включив эти функции, мы можем лучше фиксировать динамику данных временных рядов.

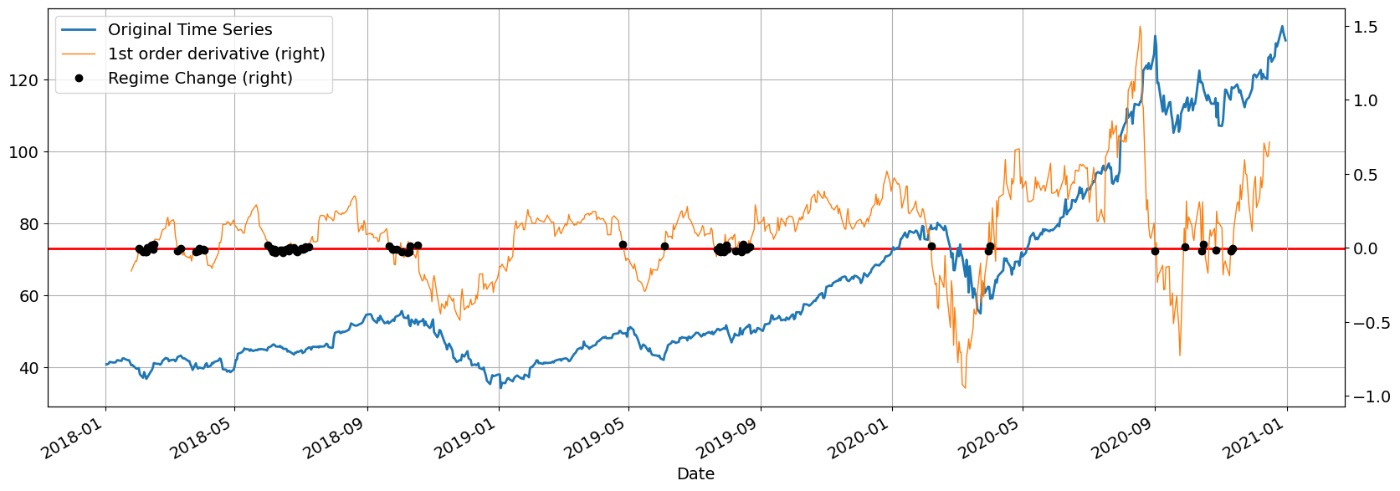
Производная первого порядка представляет собой мгновенную скорость изменения переменной во времени. Это может помочь определить направление и величину тренда в данных. Как показано на слайде, его можно использовать в качестве маркера для обнаружения изменений в режимах акций или поведения рынка.

Производная второго порядка представляет скорость изменения производной первого порядка. Это может помочь определить ускорение или замедление тренда и выявить точки перегиба.

Кроме того, здесь необходимо упомянуть Сезонные производные и Перекрестные производные: помогают фиксировать сезонные колебания данных и влияние парных переменных.

Чтобы вычислить производные, мы можем использовать метод конечных разностей:

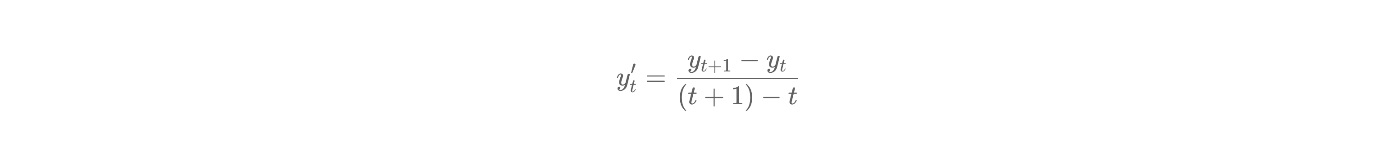
Самый простой способ вычислить первую производную с помощью pandas и использовать в качестве функции:

time_series = pd.Series(data, index=dates)

# Calculate the first-order derivative
time_series_diff = time_series.diff().dropna()

# Combine the original time series and the first-order derivative
data = pd.concat([time_series.shift(1), time_series_diff], axis=1).dropna()
data.columns = ['y_t', 'first_derivative']

Вот пример использования производной первого порядка в качестве индикатора смены режима. Когда производная меняет знак, это означает смену режима:

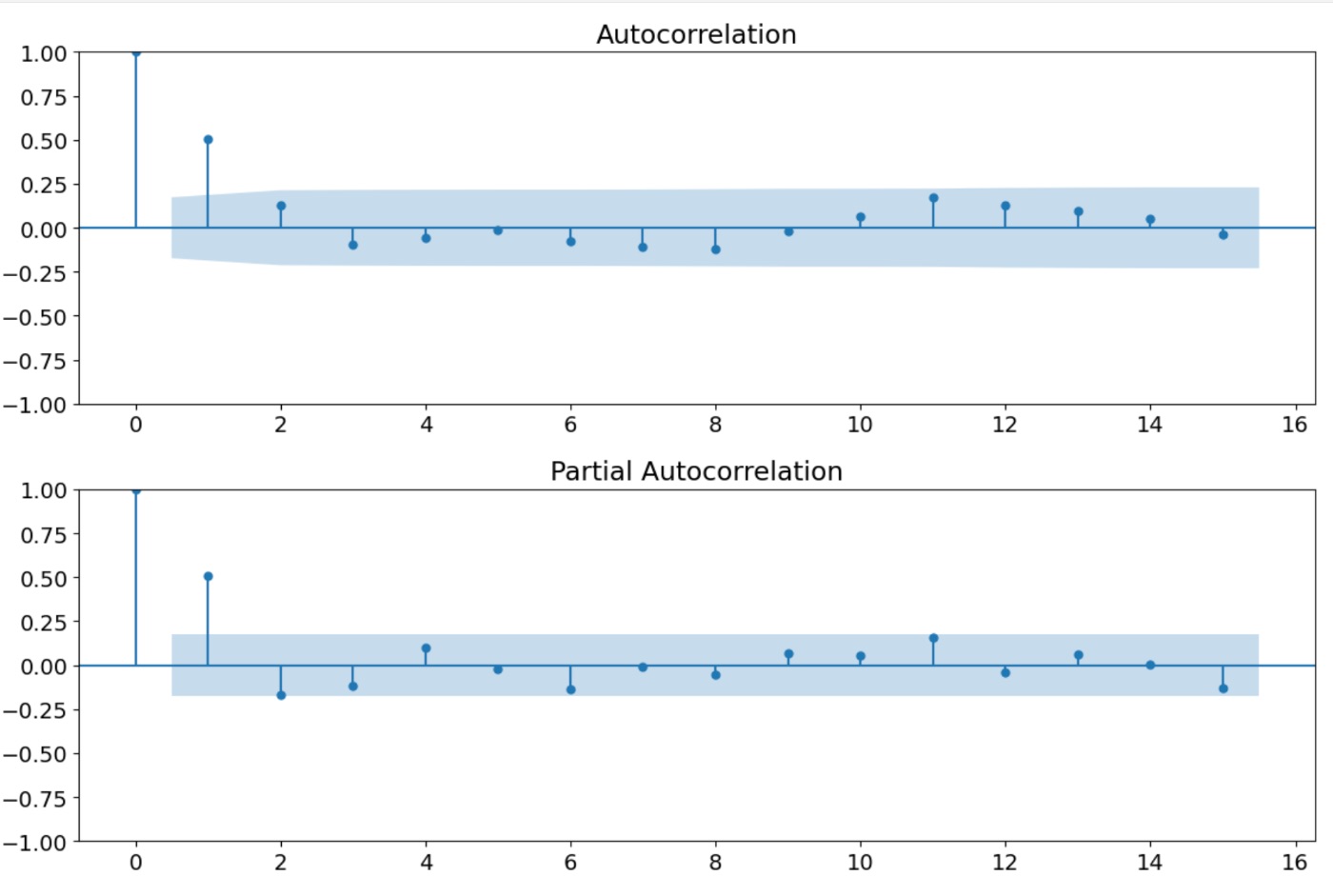
Автокорреляция и частичная автокорреляция

Автокорреляция, также известная как автоковариационная функция или последовательная корреляция, измеряет линейную зависимость между точками данных временного ряда с разным запаздыванием.

С другой стороны, частичная автокорреляция, также известная как функция частичной автоковариации, измеряет корреляцию между двумя точками данных с разным запаздыванием после устранения влияния других точек данных с меньшими задержками.

Пример кода для автокорреляции и частичной автокорреляции:

from statsmodels.tsa.stattools 
import acf, pacf 
data = np.array([...])  
# Input time series data 
lags = 10 
autocorr = acf(data, nlags=lags) 
partial_autocorr = pacf(data, nlags=lags)

f, ax = plt.subplots(nrows=2, ncols=1, figsize=(width, 2*height))
plot_acf(data,lags=lag_acf, ax=ax[0])
plot_pacf(data,lags=lag_pacf, ax=ax[1], method='ols')
plt.tight_layout()
plt.show()

Заключение

Расширенные методы разработки признаков для данных временных рядов могут значительно повысить производительность моделей машинного обучения.

Преобразование Фурье, вейвлет-преобразование, производные и автокорреляция вносят уникальный вклад в понимание лежащей в основе структуры и тенденций временных данных.

Используя эти методы, аналитики могут создавать более точные и эффективные модели прогнозирования, что в конечном итоге приводит к более эффективному принятию решений в различных областях.