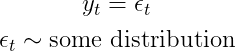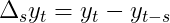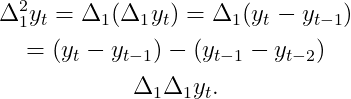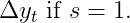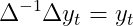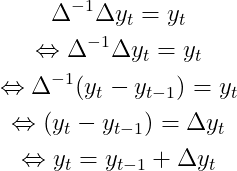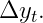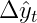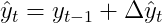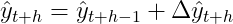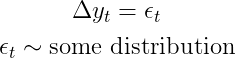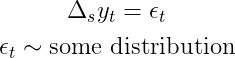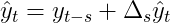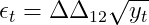Руководство Data Scientist по упрощенным моделям временных рядов
18 мая 2023 г.Отказ от ответственности. Название в значительной степени вдохновлено это отличный разговор; Фото Томаса Борманса из Unsplash
Как следует из названия, сегодня мы хотим рассмотреть почти тривиально простые модели. Хотя текущая тенденция указывает на сложные модели, даже для моделей временных рядов, я все еще верю в простоту. В частности, когда ваш набор данных невелик, могут быть полезны последующие идеи.
Справедливости ради, эта статья, вероятно, будет наиболее полезна для людей, которые только начинают заниматься анализом временных рядов. Все остальные должны сначала ознакомиться с содержанием и решить для себя, хотят ли они продолжать.
Лично я до сих пор весьма заинтригован тем, как далеко можно продвинуть даже самые упрощенные модели временных рядов. В следующих абзацах представлены некоторые идеи и мысли, которые я собирал по этой теме с течением времени.
Модели с чистым i.i.d. шум
Мы начнем с самого простого (вероятностного) способа моделирования (одномерного) временного ряда. А именно, мы хотим взглянуть на простую iнезависимо, iдентично, dраспределенную случайность:
Это означает, что все наши наблюдения имеют одинаковое распределение в любой момент времени (одинаковое распределение). Что еще более важно, мы предполагаем отсутствие взаимосвязи между наблюдениями (независимо). Очевидно, что это также исключает любые авторегрессивные термины.
Возможно, ваш первый вопрос заключается в том, не являются ли такие модели слишком упрощенными, чтобы их можно было использовать для решения реальных проблем. Конечно, большинство временных рядов вряд ли имеют статистическую связь со своим прошлым.
Хотя эти опасения во всех смыслах верны, тем не менее мы можем сделать следующие выводы:
<цитата>Любая модель временных рядов, более сложная, чем модель чистого шума, также должна давать более точные прогнозы, чем модель чистого шума.
Короче говоря, мы можем по крайней мере использовать случайный шум в качестве эталонной модели. Возможно, нет более простого подхода к созданию базовых тестов, чем этот. Даже методы сглаживания, скорее всего, потребуют настройки большего количества параметров.
Помимо этого довольно очевидного варианта использования, есть еще одно потенциальное применение i.i.d. шум. Благодаря своей простоте модели шума могут быть полезны для очень небольших наборов данных. Учтите следующее: если для больших и сложных моделей требуются большие наборы данных для предотвращения переобучения, то для простых моделей требуется лишь небольшое количество данных.
Конечно, можно спорить о том, какой размер набора данных можно считать «маленьким».
Встроенный i.i.d. шум
Теперь все становится интереснее. В то время как необработанный i.i.d. шум не может объяснить автокорреляцию между наблюдениями, интегрированный шум может. Прежде чем приступить к демонстрации, давайте познакомимся с оператором разности:
Если вы еще не слышали о разностных задачах для временных рядов, отлично! Если да, то, надеюсь, вы все еще можете узнать что-то новое.
Определение интегрированного временного ряда
С помощью оператора разности в нашем наборе инструментов мы теперь можем определить интегрированные временные ряды:
В этом определении есть несколько идей, которые следует уточнить:
Во-первых, вы, вероятно, заметили концепцию возведения в степень разностного оператора. Вы можете просто думать об этом как о выполнении дифференцирования несколько раз. Для оператора квадрата разности это будет выглядеть следующим образом:
Как мы увидим, несколько разностных операторов позволяют нам одновременно обрабатывать разные шаблоны временных рядов.
В-третьих, принято просто писать
Мы с радостью примем это соглашение здесь. Кроме того, мы называем такие временные ряды просто интегрированными без ссылки на их порядок или сезонность.
Очевидно, что нам также необходимо повторно преобразовать разностное представление обратно в его исходный домен. В наших обозначениях это означает, что мы инвертируем разностное преобразование, т.е.
должен выполняться для произвольных разностных преобразований. Если мы расширим эту формулу, мы получим
Эти упрощения следуют из того факта, что разностный оператор является линейным оператором (здесь мы не будем вдаваться в подробности). Технически, последнее уравнение просто говорит о том, что следующее наблюдение является суммой этого наблюдения плюс дельта.
В задаче прогнозирования у нас обычно есть прогноз изменения
Обозначим этот прогноз как
подчеркнуть, что это не фактическое изменение, а прогнозируемое. Таким образом, прогноз для интегрированного временного ряда
После этого мы рекурсивно применяем эту логику настолько далеко в будущее, насколько должен идти наш прогноз:
Интегрированный шум для кажущихся сложными узоров
К настоящему времени вы, вероятно, можете себе представить, что подразумевается под интегрированной моделью шума. На самом деле, мы можем создать бесчисленное множество вариантов интегрированной модели шума, просто объединив несколько разностных операторов со случайным шумом.
Линейные тренды из интегрированных временных рядов
Одной из возможностей может быть просто интегрированный временной ряд, т. е.
Интересно смоделировать данные такой модели с помощью простого стандартного нормального распределения.
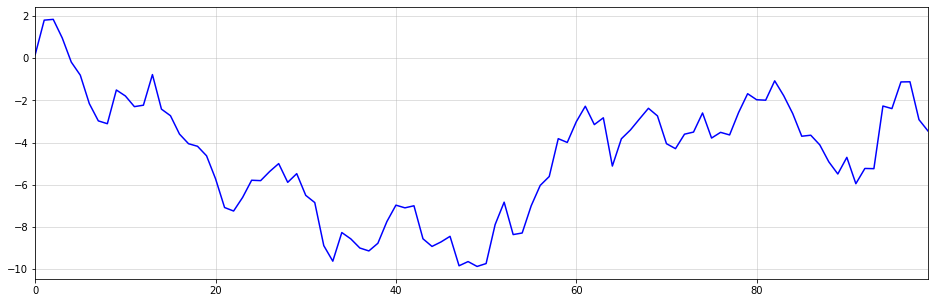
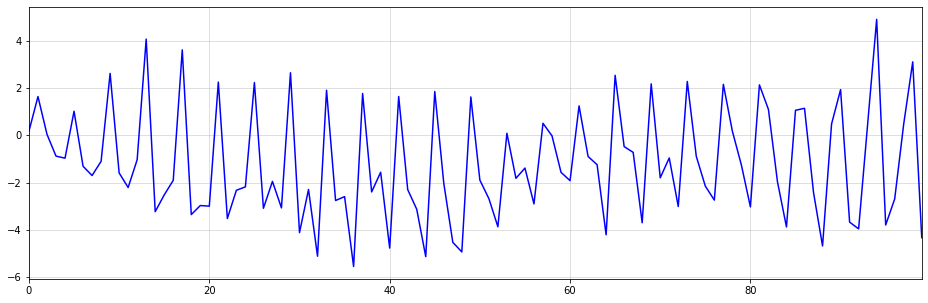
Как оказалось, выборки из этого временного ряда демонстрируют линейные тренды с потенциальными точками изменения. Однако ясно, что эти тенденции и точки изменения возникают совершенно случайно.
Это означает, что простая подгонка кусочно-линейных функций для прогнозирования таких тенденций может быть опасным подходом. В конце концов, если изменения происходят случайным образом, то все линейные линии тренда являются просто артефактами случайного процесса генерации данных.
Тем не менее, в качестве важной оговорки, "непредсказуемый" означает непредсказуемый из самого временного ряда. Внешняя функция все еще может точно прогнозировать потенциальные точки изменения. Однако здесь мы предполагаем, что временные ряды являются нашим единственным доступным источником информации.
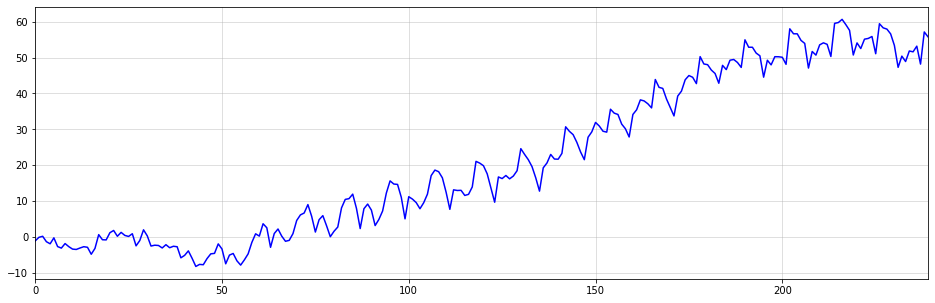
Ниже вы можете увидеть пример описанного явления. Хотя кажется, что изменение тренда происходит около t=50, это изменение является чисто случайным. Восходящий тренд после t=50 также останавливается около t=60. Представьте, как бы работала ваша модель, если бы вы экстраполировали восходящий тренд после t = 60.
Конечно, даже в таких условиях говорят «никогда не говори никогда». Тем не менее, если вы применяете такие модели, вы действительно должны знать, что делаете.
Сезонные модели
Подобно тому, как простая интеграция создает тенденции, мы также можем создавать сезонные закономерности:
Формально нам теперь нужно, чтобы s-я разность нашего сезонного процесса была стационарной, например,
Обратная операция — преобразование i.i.d. процесс обратно к сезонной интеграции - работает аналогично предыдущему:
Об операции, обратной сезонным различиям, можно думать как об операции cumsum за периоды s. Поскольку я не знаю о соответствующей встроенной функции Python, я решил выполнить reshape->cumsum->reshape, чтобы получить желаемый результат. Ниже приведен пример с s=4:
Как видите, сгенерированный временной ряд выглядит достаточно реалистично. Мы могли бы легко продать это как квартальные данные о продажах какого-либо продукта ничего не подозревающему специалисту по данным.
Мы могли бы даже объединить оба типа интеграции, чтобы создать сезонный временной ряд с трендовым поведением:
К этому моменту вы, вероятно, поймете, что название этой статьи было немного кликбейтным. Интегрированные временные ряды, по сути, являются чисто линейными моделями. Однако я считаю, что большинство людей не считают модель с более или менее нулевыми параметрами типичной линейной моделью.
Эффекты памяти благодаря интеграции
Еще одним интересным свойством интегрированных временных рядов является возможность моделировать эффекты памяти.
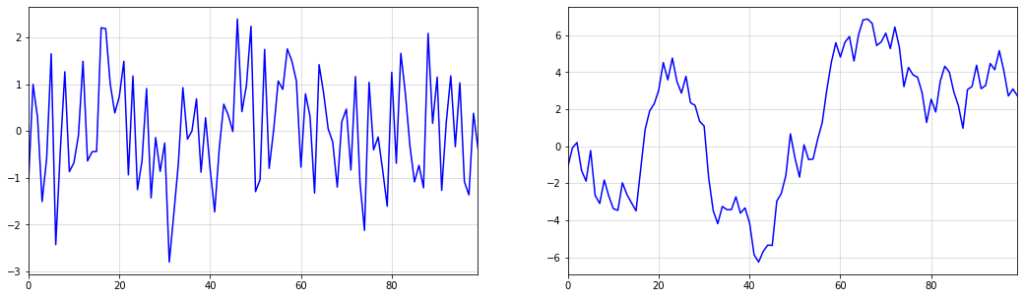
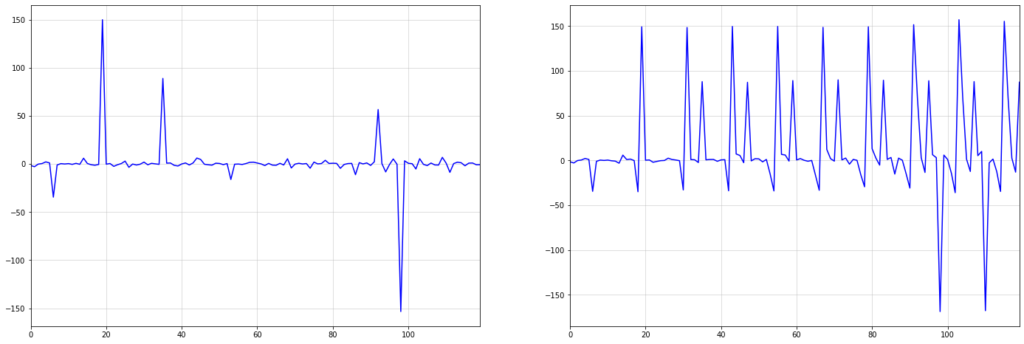
Этот эффект особенно хорошо заметен, когда в наших данных есть более крупные шоки или выбросы. Рассмотрим приведенный ниже пример, который показывает сезонную интеграцию порядка s=12 по i.i.d. взято из стандартного распределения Коши:
Первый большой шок в i.i.d. Ряд Коши около t = 20 сохраняется по всему интегрированному ряду справа. Со временем происходят новые потрясения, которые также являются устойчивыми.
Это свойство памяти может быть очень полезным на практике. Например, экономические потрясения, вызванные пандемией, вызвали стойкие изменения во многих временных рядах.
Сравнение с NBEATS и NHITS
Теперь воспользуемся набором данных AirPassengers из neuralforecast компании Nixtla. для быстрой оценки вышеизложенных идей. Если вы регулярно читаете мои статьи, возможно, вы помните общую процедуру из этот.
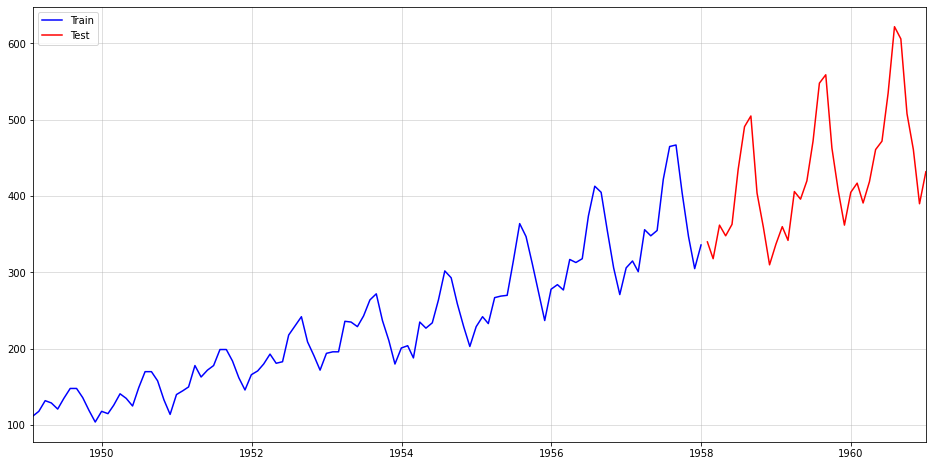
Во-первых, мы разделяем данные на обучающий и тестовый периоды, причем последний состоит из данных за 36 месяцев:
https://gist.github.com/SaremS/510303feb5c1eef012ba7075930f4fba?embedable=true #file-airpass_data-py
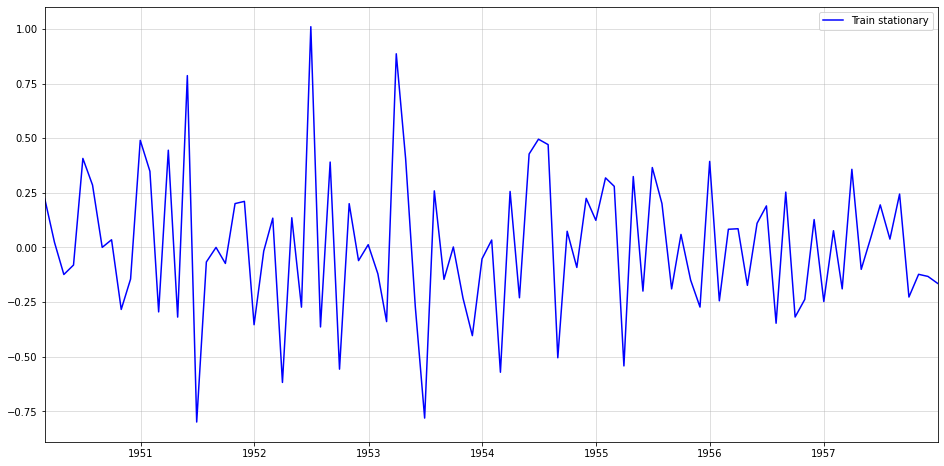
Чтобы получить стационарное, i.i.d. ряда выполняем следующее преобразование:
Во-первых, квадратный корень стабилизирует растущую дисперсию. Затем два дифференциальных оператора удаляют сезонность и тенденцию. Для соответствующего повторного преобразования проверьте код ниже.
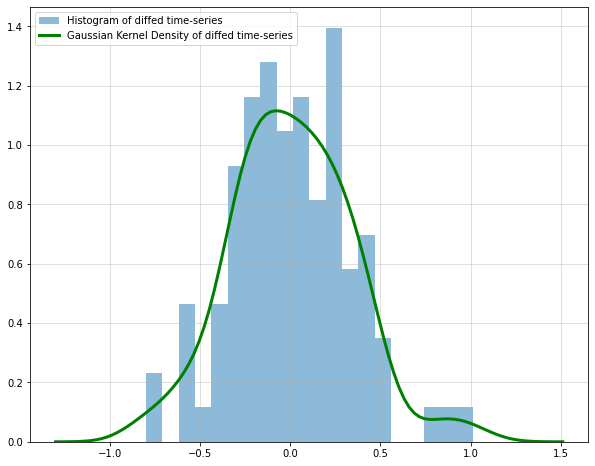
Мы также можем проверить гистограмму и график плотности стабилизированного временного ряда:
Наш стационарный ряд также выглядит несколько нормально распределенным, что всегда является хорошим свойством.
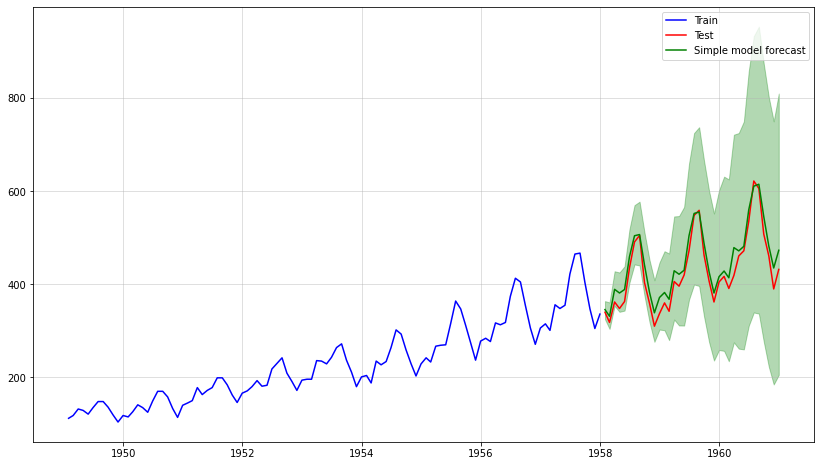
Теперь создадим прогноз на тестовый период. Предполагая, что мы не знаем точного распределения нашего i.i.d. серии, мы просто используем эмпирическое распределение с помощью обучающих данных.
Следовательно, мы моделируем будущие значения путем повторного интегрирования случайных выборок из эмпирических данных:
Это выглядит очень хорошо — средний прогноз очень близок к тестовым данным. Кроме того, наше моделирование позволяет нам эмпирически выбрать все распределение прогноза. Поэтому мы также можем легко добавить доверительные интервалы.
Наконец, давайте посмотрим, как наш подход сравнивается с довольно сложными моделями временных рядов. Для этого я воспользовался реализацией Nixtla NBEATS и NHITS:
Ниже приведены соответствующие RMSE для набора тестов:
* Простая модель: 25,5021 * NBEATS: 42,6277 * НВИЦ: 62,6822 *
Как мы видим, наша почти тривиальная модель значительно превзошла две сложные модели временных рядов. Конечно, мы должны подчеркнуть, что это не позволяет делать какие-либо общие выводы.
Скорее, я ожидаю, что нейронные модели превзойдут наш простой подход для больших наборов данных. Тем не менее, в качестве эталона эти тривиальные модели всегда заслуживают внимания.
Выводы. Что мы из этого делаем?
Как неоднократно говорилось в этой статье:
<цитата>На первый взгляд сложные временные ряды все же могут следовать довольно простому процессу генерации данных.
В конце концов, вы можете потратить часы, пытаясь подогнать слишком сложную модель, даже если основная проблема почти тривиальна. В какой-то момент кто-то может прийти, подобрать простой ARIMA(1,0,0) и все же превзойти вашу сложную нейронную модель.
Чтобы избежать описанного выше наихудшего сценария, рассмотрите следующую идею:
<цитата>Приступая к решению новой задачи временных рядов, всегда начинайте с самой простой из возможных моделей и используйте ее в качестве эталона для всех остальных моделей.
Хотя это общеизвестно в сообществе специалистов по науке о данных, я считаю, что в данном контексте это заслуживает особого внимания. Особенно из-за сегодняшней (в некоторой степени оправданной) шумихи вокруг глубокого обучения может возникнуть соблазн начать прямо с чего-то необычного.
Для многих проблем это может быть правильным путем. Сегодня никто не стал бы рассматривать Скрытую Марковскую модель для НЛП, когда вложения LLM теперь доступны почти бесплатно.
Однако, как только ваш временной ряд станет большим, современное машинное обучение, вероятно, станет лучше. В частности, для таких масштабных задач очень популярны Gradient Boosted Trees. .
Как вы уже догадались, более спорным подходом было бы глубокое обучение для временных рядов. Хотя некоторые люди считают, что эти модели здесь не работают, их популярность на технологические фирмы, такие как Amazon, вероятно, говорят сами за себя.
Ссылки
[1] Гамильтон, Джеймс Дуглас. Анализ временных рядов. Издательство Принстонского университета, 2020 г.
[2] Хайндман, Роб Дж., & Атанасопулос, Джордж. Прогнозирование: принципы и практика. Отексты, 2018 г.
Оригинал