Руководство для начинающих по структурам данных и алгоритмам

Структуры данных и алгоритмы — это фундаментальные концепции информатики. Они относятся к организации и манипулированию данными таким образом, чтобы они были эффективными и результативными. Изучение структур данных и алгоритмов позволяет писать более качественный код, решать сложные проблемы и понимать внутреннюю работу компьютерных программ.

n В этом руководстве мы рассмотрим основы структур данных и алгоритмов, включая общие структуры данных, базовые алгоритмы и расширенные алгоритмы. Мы также обсудим такие важные понятия, как временная и пространственная сложность, а также использование нотации Big O для анализа производительности алгоритмов.

Во-первых, давайте обсудим, что такое структуры данных и алгоритмы и почему они важны.

Структуры данных — это способ организации и хранения данных, обеспечивающий эффективный доступ к ним и их изменение. Общие структуры данных включают массивы, списки, стеки, очереди, деревья и графики. Каждая структура данных имеет свои сильные и слабые стороны, а подходящая структура данных для использования зависит от конкретных потребностей решаемой проблемы.

Алгоритмы — это наборы инструкций для решения конкретной задачи. Они могут быть реализованы с использованием одной или нескольких структур данных, а эффективность алгоритма зависит от выбранных структур данных и шагов, предпринятых для решения проблемы. Некоторые распространенные алгоритмы включают алгоритмы поиска, алгоритмы сортировки и алгоритмы графов.

Структуры данных и алгоритмы важны, потому что они обеспечивают основу для многих вещей, которые мы делаем на компьютерах. Независимо от того, работаете ли вы над небольшим проектом или над крупномасштабной программной системой, понимание структур данных и алгоритмов поможет вам максимально эффективно использовать ресурсы и добиться максимально возможной производительности.

В следующем разделе мы рассмотрим некоторые основные понятия, необходимые для понимания структур данных и алгоритмов, такие как временная и пространственная сложность и использование нотации Big O.

Большая нотация O

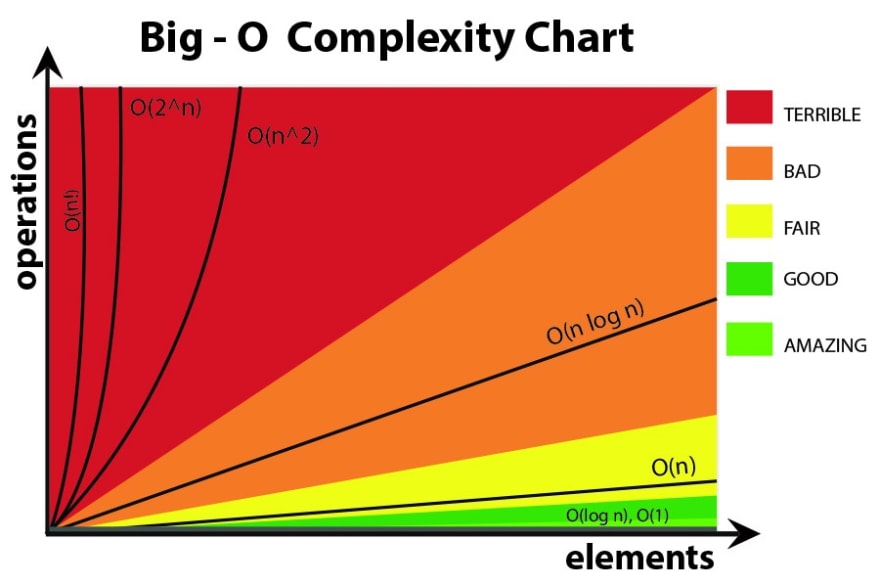
Нотация Big O — это способ описания роста производительности алгоритма по мере увеличения размера входных данных. Он обеспечивает общее представление об эффективности алгоритма, позволяя нам сравнивать производительность различных алгоритмов, не увязая в деталях.

В общем, мы говорим, что алгоритм имеет производительность O (f (n)), если количество выполняемых им операций не более чем постоянно кратно f (n) по мере роста размера входных данных n. Например, если алгоритм имеет производительность O(n^2), это означает, что количество выполняемых им операций не более чем константа, кратная n^2, где n – размер входных данных.

Функция f(n) в нотации Big O называется временной сложностью алгоритма. Он говорит нам, как количество операций, выполняемых алгоритмом, растет по мере увеличения размера входных данных. Общие временные сложности включают O (1) (постоянное время), O (log n) (логарифмическое время), O (n) (линейное время), O (n log n) (линейное арифмическое время) и O (n ^ 2) (квадратичное время).

Обозначение Big O полезно, поскольку позволяет сравнивать производительность различных алгоритмов, не увязая в деталях их реализации. Например, если у нас есть два алгоритма с производительностью O(n^2), мы знаем, что они оба будут иметь одинаковые характеристики производительности, даже если один алгоритм намного быстрее другого на небольших входных данных.

В целом, нам нужны алгоритмы с минимально возможной временной сложностью, поскольку они будут наиболее эффективными и смогут обрабатывать большие входные данные, не занимая слишком много времени на выполнение. Однако важно помнить, что временная сложность алгоритма — это только один фактор, который следует учитывать при выборе алгоритма. Другие факторы, такие как объемная сложность алгоритма (сколько памяти он требует) и простота реализации, также могут быть важны.

Сложность времени и пространства

Временная и пространственная сложность — два важных показателя производительности алгоритма. Под временной сложностью понимается количество времени, необходимое для завершения алгоритма, а под пространственной сложностью понимается требуемый объем памяти или дискового пространства.

Мы хотим, чтобы алгоритмы были максимально эффективными с точки зрения времени и пространства. Это означает, что они должны решать поставленную задачу за кратчайшее время и с наименьшим использованием памяти.

Чтобы проанализировать временную и пространственную сложность алгоритма, мы используем нотацию, называемую «нотация Big O». Это обозначение дает нам способ выразить верхнюю границу временной или пространственной сложности алгоритма.

Например, если алгоритм имеет временную сложность O(n), это означает, что время, необходимое для завершения, растет линейно с размером входных данных (n). Алгоритм с временной сложностью O(n^2) растет квадратично с размером входных данных, а алгоритм с временной сложностью O(log n) растет логарифмически с размером входных данных.

Пространственная сложность алгоритма обычно выражается с помощью нотации Big O. Например, алгоритм с пространственной сложностью O(1) использует постоянный объем памяти, независимо от размера входных данных. Алгоритм с пространственной сложностью O(n) использует площадь, которая линейно растет с размером входных данных, а алгоритм с пространственной сложностью O(n^2) использует пространство, которое растет квадратично с размером входных данных.

Обычно мы хотим, чтобы алгоритмы имели минимально возможную временную и пространственную сложность. Это означает, что они должны быть максимально эффективными, используя наименьшее количество времени и пространства для решения проблемы. В следующем разделе мы обсудим некоторые распространенные структуры данных и то, как они используются в алгоритмах.

Существует множество различных структур данных, которые обычно используются в алгоритмах, и конкретная используемая структура данных часто зависит от конкретной проблемы, которую пытается решить алгоритм. Некоторые распространенные структуры данных включают массивы, связанные списки, стеки, очереди, деревья и графики.

Массивы

Это одна из самых основных структур данных, состоящая из набора элементов, которые хранятся в непрерывном блоке памяти. Массивы используются для хранения данных одного типа, и доступ к ним осуществляется с помощью индекса. Массивы — это очень эффективная структура данных для хранения и доступа к данным, и они обычно используются во многих алгоритмах.

Связанный список

Связанные списки — еще одна распространенная структура данных, состоящая из ряда узлов, соединенных между собой ссылками. Каждый узел содержит значение и указатель на следующий узел в списке. Связанные списки часто используются, когда размер данных заранее неизвестен или когда данные необходимо вставить или удалить в середине списка.

Стеки и очереди

Стеки и очереди – это структуры данных, основанные на принципах "последний пришел, первый вышел" (LIFO) и "первый пришел, первый ушел" (FIFO) соответственно. В стеке элементы добавляются и удаляются из верхней части стека, а в очереди элементы добавляются в конец и удаляются из начала. Стеки и очереди обычно используются в алгоритмах хранения и организации данных.

Деревья

Деревья – это иерархические структуры данных, состоящие из корневого узла и нуля или более дочерних узлов. Каждый дочерний узел может иметь свои собственные дочерние узлы, создавая древовидную структуру. Деревья часто используются для представления иерархических отношений, таких как структура файловой системы.

Графики

Графики — это еще одна распространенная структура данных, состоящая из набора вершин (или узлов) и соединяющих их ребер. Графики используются для представления взаимосвязей между объектами и обычно используются в алгоритмах для таких задач, как анализ сети и планирование маршрута.

Хеш-таблицы

Хэш-таблица – это структура данных, используемая для быстрого хранения и извлечения данных. Он работает, сохраняя данные в структуре, подобной массиву, используя хеш-функцию для сопоставления каждой части данных с определенным индексом в массиве. Когда данные вставляются в хеш-таблицу, хэш-функция используется для вычисления индекса, в котором данные должны храниться, а затем данные помещаются в этот индекс в массиве.

Для извлечения данных из хэш-таблицы та же хеш-функция используется для вычисления индекса, в котором должны располагаться данные, а затем данные извлекаются из этого индекса в массиве. Хеш-таблицы очень эффективны для хранения и извлечения данных и широко используются во многих алгоритмах.

Они особенно полезны для реализации структур данных, таких как наборы и карты, где целью является быстрое хранение и извлечение данных. Хэш-таблицы также часто используются в системах баз данных и других приложениях, где важен быстрый доступ к данным.

Кучи

Куча — это специализированная структура данных, которая используется для хранения набора данных в определенном порядке. Существует два типа куч: мини-кучи и макс-кучи. В минимальной куче наименьший элемент всегда находится в корне кучи, а в максимальной куче самый большой элемент всегда находится в корне.

Кучи часто используются в алгоритмах, требующих быстрого доступа к наименьшему (или самому большому) элементу в наборе данных. Например, структура данных кучи обычно используется в алгоритмах сортировки, поиска минимального или максимального элемента в наборе и реализации приоритетных очередей.

Чтобы поддерживать порядок данных в куче, элементы добавляются и удаляются в соответствии с набором правил. Когда элемент добавляется в кучу, он сначала добавляется в конец кучи, а затем сравнивается с его родительским узлом. Если элемент меньше (или больше), чем его родитель, он заменяется своим родителем. Этот процесс продолжается до тех пор, пока элемент не окажется в правильном положении в куче.

Когда элемент удаляется из кучи, он сначала заменяется последним элементом в куче, а затем сравнивается с его дочерними элементами. Если элемент больше (или меньше), чем любой из его дочерних элементов, он заменяется самым маленьким (или самым большим) дочерним элементом. Этот процесс продолжается до тех пор, пока элемент не окажется в правильном положении в куче.

Кучи — это эффективная структура данных для хранения набора данных в определенном порядке, и они обычно используются во многих алгоритмах.

Существует множество различных алгоритмов, которые используются для решения широкого круга задач, и конкретный используемый алгоритм часто зависит от конкретной проблемы, которую необходимо решить. Некоторые основные алгоритмы, которые обычно используются, включают

* Алгоритмы сортировки. Эти алгоритмы используются для переупорядочения набора данных в определенном порядке, например в порядке возрастания или убывания. Примеры алгоритмов сортировки включают сортировку слиянием, сортировку вставками, быструю сортировку, сортировку кучи и сортировку подсчетом.

* Алгоритмы поиска. Эти алгоритмы используются для поиска определенной части данных в наборе данных. Примеры алгоритмов поиска включают бинарный поиск.

* Алгоритмы поиска пути. Эти алгоритмы используются для поиска кратчайшего или наиболее эффективного пути между двумя точками на графике или в другой структуре данных. Примеры алгоритмов поиска пути включают алгоритм Дейкстры и алгоритм A* (A-star).

* Рекурсия: это распространенный метод программирования, который включает определение функции в терминах самой себя, обычно путем вызова самой себя с использованием упрощенной версии исходной задачи. Рекурсия часто используется для решения проблем, которые можно разделить на более мелкие, похожие подзадачи.

* Динамическое программирование. Это метод решения сложных проблем путем их разбиения на более мелкие подзадачи и сохранения решений этих подзадач, чтобы их можно было использовать повторно. Динамическое программирование часто используется для решения задач с перекрывающейся структурой подзадач, когда одна и та же подзадача решается несколько раз.

В дополнение к основным алгоритмам, упомянутым выше, существует множество других более сложных алгоритмов, которые обычно используются для решения более сложных задач. Некоторые примеры продвинутых алгоритмов включают

Графические алгоритмы

Это класс алгоритмов, специально предназначенных для работы с графами. Граф — это структура данных, состоящая из набора вершин (или узлов) и соединяющих их ребер. Графики используются для представления взаимосвязей между сущностями и широко используются во многих областях, включая информатику, математику и инженерное дело.

Некоторые распространенные графовые алгоритмы включают

* Алгоритмы кратчайшего пути. Эти алгоритмы используются для поиска кратчайшего пути между двумя узлами в графе. Примеры алгоритмов поиска кратчайшего пути включают алгоритм Дейкстры и алгоритм A* (A-звезда).

* Алгоритмы минимального остовного дерева. Эти алгоритмы используются для нахождения минимального остовного дерева графа, которое представляет собой подмножество ребер графа, соединяющее все узлы с минимальным общим весом ребер. Примеры алгоритмов минимального остовного дерева включают алгоритм Крускала и алгоритм Прима.

* Поиск в ширину (BFS) и поиск в глубину (DFS): это два алгоритма обхода графа. Оба алгоритма начинают с определенного узла на графе и исследуют соседние узлы, но они различаются порядком, в котором они исследуют узлы.

В BFS алгоритм исследует узлы в графе по одному уровню за раз, начиная с узла в корне графа и затем двигаясь к соседним узлам, затем к следующему уровню соседей и так далее. BFS удобна для поиска кратчайшего пути между двумя узлами в графе и может быть реализована с использованием структуры данных очереди.

В DFS алгоритм исследует узлы в графе в глубину, начиная с узла в корне графа и затем перемещаясь к одному из дочерних узлов, затем к одному из дочерних элементов и так далее. DFS удобна для обхода всего графа и может быть реализована с использованием структуры данных стека. BFS и DFS — это широко используемые алгоритмы для обхода графов, и они часто используются в качестве строительных блоков для других алгоритмов, работающих с графами.

Np-сложные и Np-полные задачи

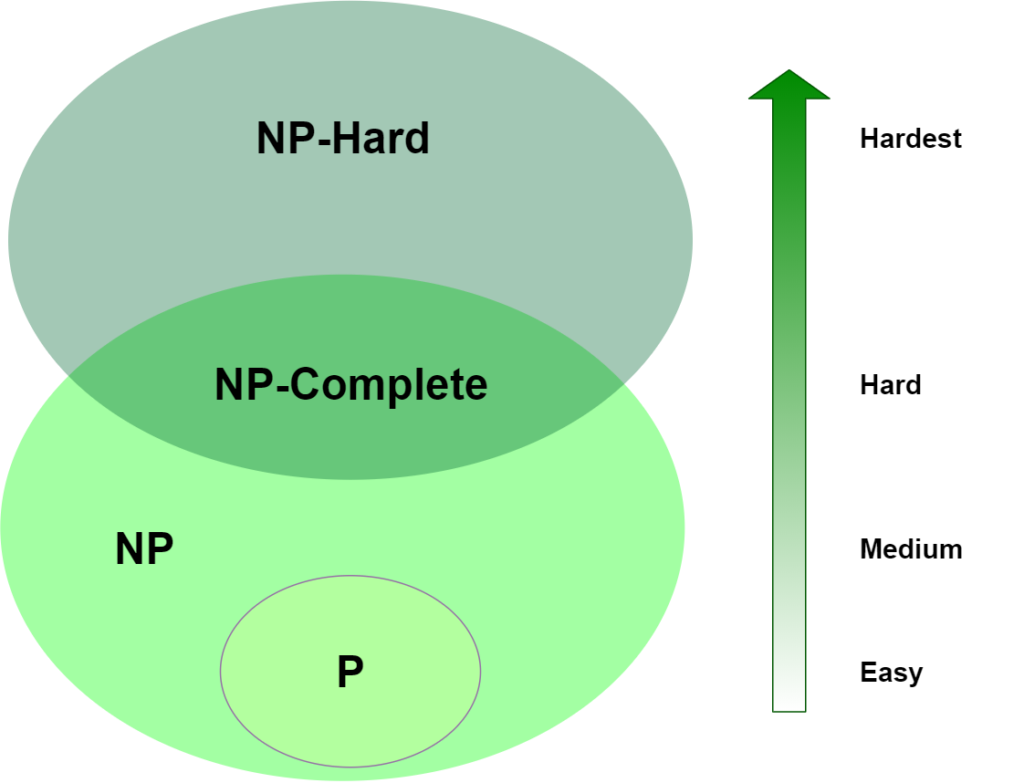
В информатике сложность проблемы — это мера количества вычислительных ресурсов (таких как время и пространство), необходимых для ее решения. Известно, что некоторые проблемы можно решить за разумное количество времени и пространства, в то время как другие известны как неразрешимые, а это означает, что не известно никакого эффективного решения.

NP-трудные и NP-полные задачи — это два типа неразрешимых задач, которые представляют особый интерес для информатики. Эти проблемы определяются в терминах класса алгоритмов, называемых недетерминированными алгоритмами с полиномиальным временем или NP-алгоритмами.

NP-сложная задача — это задача, которая не менее сложна, чем любая NP-полная задача. Это означает, что если будет найдено эффективное решение NP-сложной задачи, оно также решит все NP-полные задачи. Однако неизвестно, действительно ли все NP-сложные задачи являются NP-полными.

NP-полная задача — это задача, одновременно являющаяся NP-трудной и относящаяся к NP-классу. Это означает, что задача может быть решена за полиномиальное время с помощью NP-алгоритма. Однако неизвестно, могут ли какие-либо NP-полные задачи быть решены за полиномиальное время с помощью детерминированного алгоритма (алгоритма, который всегда дает один и тот же результат при одних и тех же входных данных).

Некоторые примеры NP-сложных и NP-полных задач включают задачу коммивояжера, задачу о рюкзаке и проблему выполнимости. Эти проблемы считаются неразрешимыми, но нет никаких доказательств того, что это так.

Заключение

Структуры данных и алгоритмы – это обширная и увлекательная область, в которой можно узнать гораздо больше, чем то, что описано в этом руководстве. Независимо от того, являетесь ли вы новичком, желающим изучить основы, или опытным программистом, стремящимся углубить свое понимание, существует множество доступных ресурсов, которые помогут вам узнать больше о структурах данных и алгоритмах.

Обзор ключевых моментов

• Структуры данных — это способы организации и хранения данных на компьютере.
• К общим структурам данных относятся массивы, связанные списки, стеки, очереди, деревья и графики.
• Алгоритмы — это наборы шагов для решения проблем.
• Основные алгоритмы включают сортировку, поиск и рекурсию.
• Расширенные алгоритмы включают машинное обучение, генетические алгоритмы и искусственный интеллект.
• Алгоритмы графов – это специализированные алгоритмы для работы с графами.
• NP-сложные и NP-полные задачи — это классы неразрешимых задач в информатике.

Дополнительные ресурсы для получения дополнительной информации о структурах данных и алгоритмах

Существует множество ресурсов для получения дополнительной информации о структурах данных и алгоритмах, включая книги, онлайн-учебники и курсы информатики для колледжей. Некоторые ресурсы, которые могут оказаться полезными, включают:

* Введение в алгоритмы Томаса Х. Кормена, Чарльза Э. Лейзерсона, Рональда Л. Ривеста и Клиффорда Штейна. * Структуры данных и алгоритмы на Java, Майкл Т. Гудрич и Роберто Тамассиа. * Алгоритмы Джеффа Эриксона. Алгоритмы, 4-е издание, Роберт Седжвик и Кевин Уэйн. * Руководство по проектированию алгоритмов Стивена С. Скиены. * Структуры данных и алгоритмы на Coursera, онлайн-курсе, преподаваемом Тимом Рафгарденом в Стэнфордском университете. * Структуры данных и алгоритмы в Khan Academy, сборнике онлайн-учебников и упражнений. * В разделе «Алгоритмы» онлайн-энциклопедии Википедия представлен обзор многих распространенных алгоритмов и структур данных.

В дополнение к этим ресурсам существует множество других книг, курсов и учебных пособий, посвященных структурам данных и алгоритмам. Вы можете найти дополнительные ресурсы, выполнив поиск в Интернете или обратившись за рекомендациями к тем, кто интересуется этой областью.