Алгоритм доказательства с нулевым разглашением, PLONK — Circuit: Sin7Y Tech Review (16)

Недавно мы исследовали алгоритм доказательства с нулевым разглашением — PLONK и хотели бы поделиться своим опытом обучения.

Статус кво

В последние годы один за другим появлялись различные новые алгоритмы доказательства с нулевым разглашением, каждый со своими уникальными характеристиками и преимуществами. Следующий рисунок из статьи Виталика иллюстрирует текущий статус алгоритма доказательства с нулевым разглашением.

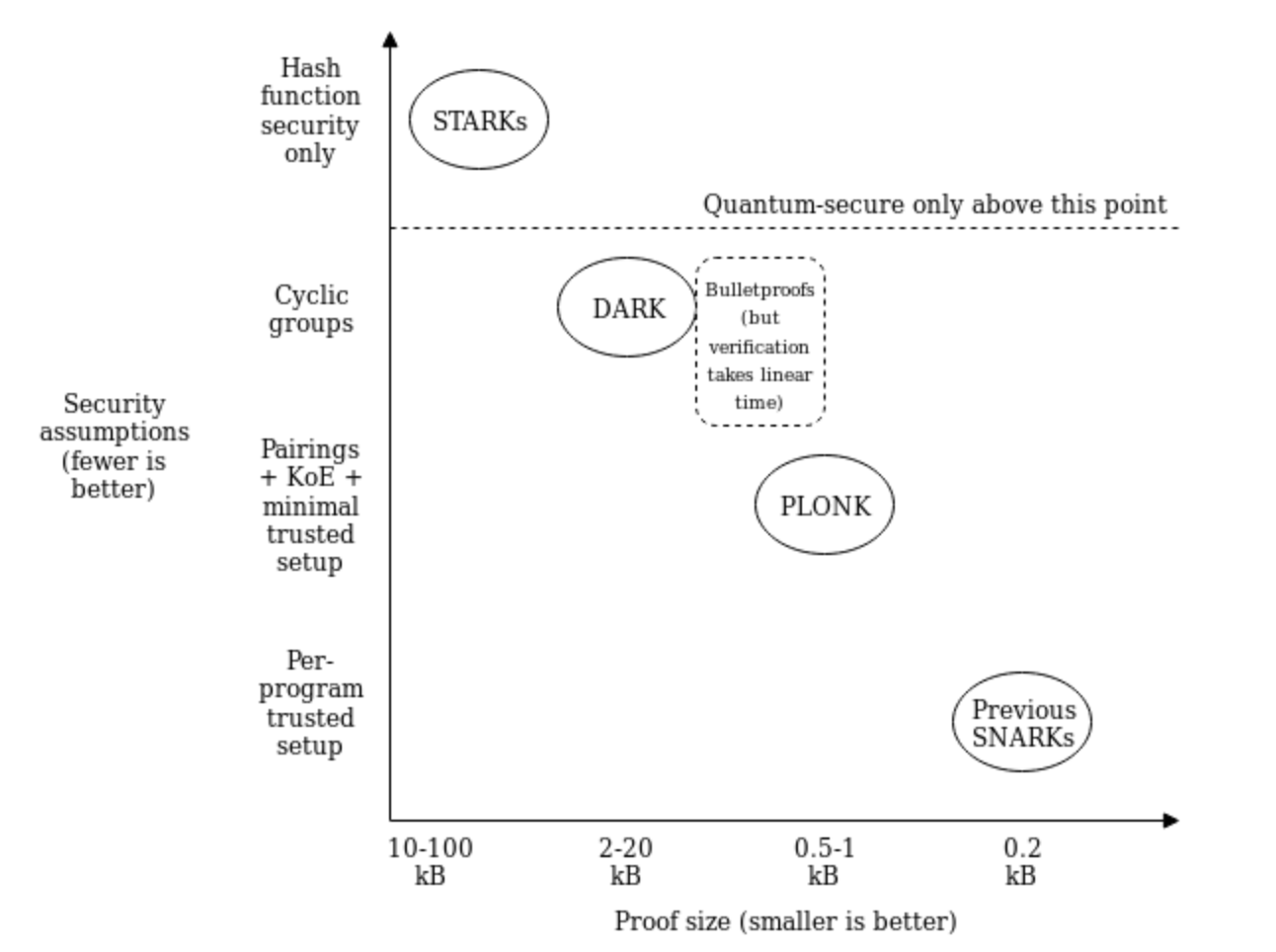
На рисунке представлены три ключевых момента:

1. Теоретически самым безопасным алгоритмом является STARK, который не опирается на допущение математических задач и является квантово-устойчивым.

1. SNARKs имеет наименьший размер Proof, такой как Groth16.

1. PLONK разработан между двумя пунктами выше, касающимися безопасности и размера доказательства.

Одной из нерешенных проблем SNARK является централизованная настройка доверия, также известная как Common Reference String (CRS). Будь то алгоритмы PGHR13, Groth16 или GM17, их CRS предназначены для одноразового использования и не подлежат обновлению. Различные проблемы будут соответствовать разным CRS, становясь более проблематичными в некоторых сценариях. Напротив, PLONK и SONIC имеют конкурентные преимущества в ответ на эти проблемы. Хотя им также требуется централизованная установка доверия, их CRS обладает определенной степенью универсальности. Пока размер цепи не превышает верхний порог CRS, некоторые задачи проверки могут совместно использовать CRS, которая называется универсальной структурированной эталонной строкой (SRS). Определение SRS см. в разделе 3 протокола SONIC.

PLONK принимает концепцию SRS SONIC, но значительно повышает эффективность доказательства. Далее мы разработаем PLONK в следующих четырех разделах:

1. Схемотехника ---- описание схемы PLONK

1. Аргумент перестановки или проверка перестановки — используйте ограничения копирования, чтобы доказать согласованность между вентилями в схеме.

1. Полиномиальное обязательство ---- эффективно доказывает правильность полиномиального уравнения

1. Анализ протокола PLONK

Схема

PLONK и SONIC имеют одинаковое описание схемы. Короче говоря, мы хотели бы поделиться двумя входами:

1. Независимо от описания схемы, схема удовлетворяет двум пунктам: справедливость отношения ограничений внутри элемента и между элементами.

1. В SNARK цепь состоит из эффективных проводов. В PLONK, SONIC и HALO схема состоит из вентилей.

Различные методы описания этих двух схем вызвали некоторые размышления. Когда мы ранее изучали SNARK, мы все верили в тот факт, что «справедливость полиномиальных уравнений доказывает, что ограничение каждого вентиля действительно», а затем делали вывод, что вся логика схемы верна. В этом процессе мы не доказали правильность согласованности между вентилями. Но в PLONK, в дополнение к проверке полиномиального уравнения, используется математический метод аргумента перестановки для проверки отношения ограничения между вентилями, то есть ограничения копирования. Почему такая разница? Не стесняйтесь обсуждать это в разделе комментариев, если это интересно. Насколько мы понимаем, разница возникает из-за разных описаний схем:

1. В PLONK вентиль — это описание схемы модуля, которое определяет свои собственные L, R и O для каждого вентиля. Следовательно, необходимо доказать согласованность между вентилями.

1. В SNARK проводник — это описание модуля, в котором значения между проводами имеют один и тот же свидетель. Поэтому нет необходимости доказывать целостность.

Аргумент перестановки

Как упоминалось в PLONK, необходимо доказать справедливость отношения ограничений между вентилями. Прежде чем объяснять конкретные принципы, мы рассмотрим процесс протокола PLONK, показанный на следующем рисунке.

![Рис. 2. Протокол PLONK] (https://cdn.hackernoon.com/images/Ns6mVt8NqgNkfsouVyus9tAe3mB2-ewb3fe3.jpeg)

На рисунке кратко показаны три точки:

1. Сгенерируйте три полинома на основе схемы, которая представляет левый вход, правый вход и выход этой схемы соответственно.

1. Используйте протокол проверки перестановки, чтобы доказать действительность отношения ограничения копирования.

1. Шаги 3 и Шаг 4 проверяют действительность отношения ограничения в пределах ворот.

Первый пункт уже был объяснен в разделе схемы. Далее мы проанализируем принципы процесса проверки полиномиальной перестановки. Мы начнем с простого сценария:

（1）Проверка перестановки одного полинома

Это нужно для того, чтобы доказать, что существуют две разные точки для конкретного многочлена f, x и y, где f(x) = f(y). Мы рассмотрим конкретные принципы.

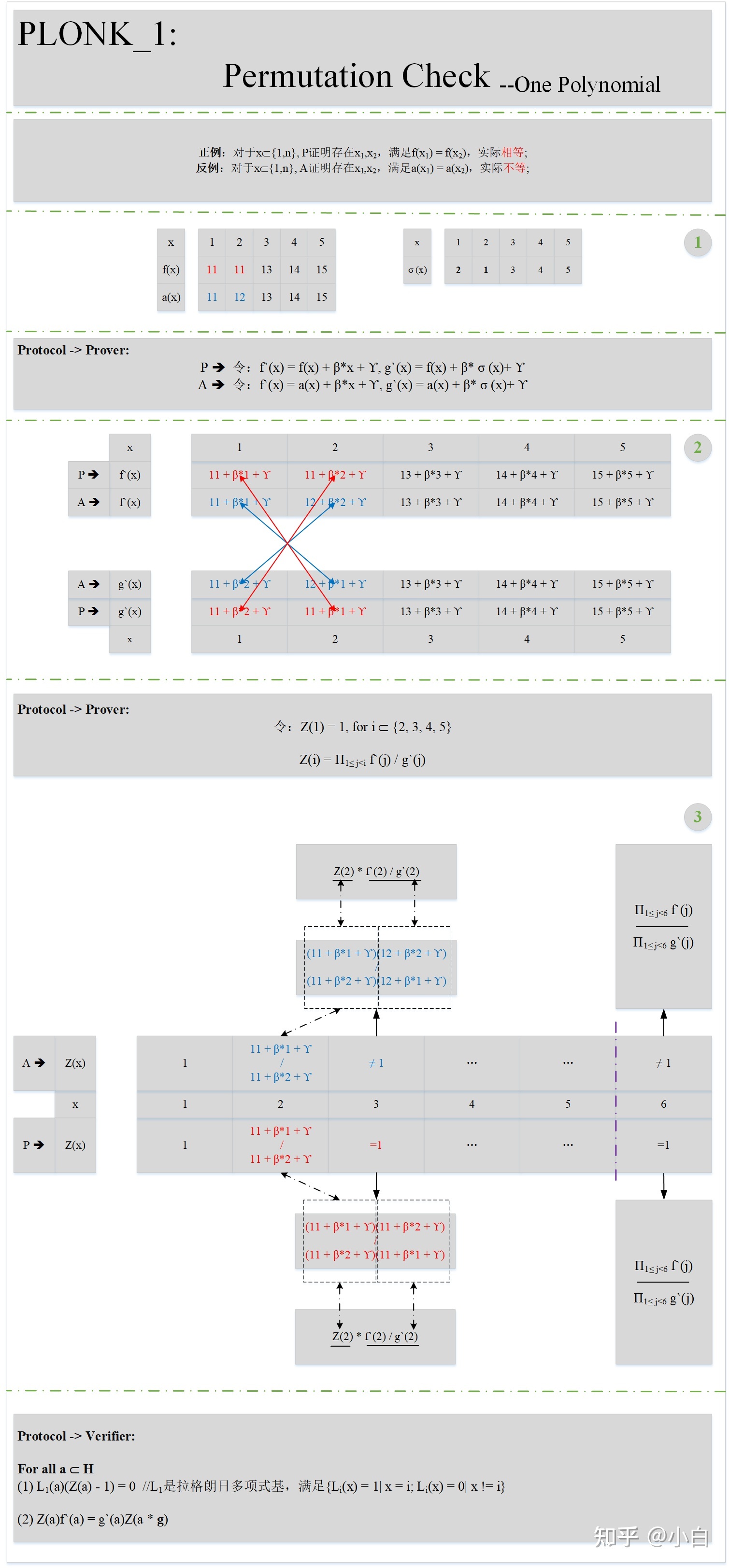
На приведенном выше рисунке пример P и контрпример A приведены для того, чтобы помочь понять принцип проверки перестановки. Есть несколько моментов, которые необходимо решить:

1. После тщательного анализа Z нетрудно обнаружить, что Z(n+1) представляет собой отношение между кумулятивным значением произведения двух функций (интересно, эквивалентно ли оно аккумулятору пар координат в статье Виталика ). Теоретически он равен 1. Следовательно, нам нужно придумать полином Z, который удовлетворяет:

1. град(Z) < п

1. Z(n+1) = 1

1. Мультипликативная циклическая группа может удовлетворять этому условию. Если мы создадим мультипликативную циклическую группу H порядка n, Z(g)=Z(g^(n+1)) можно узнать на основе свойств группы. Следовательно, при проектировании Z мы обеспечим Z(g) = 1. Значение независимой переменной на приведенном выше рисунке также изменится с {1…n} на {g…g^n}. Итак, в проверочной части рисунка выше a заменена всеми компонентами группы H.

1. Согласно протоколу в статье, полином Z будет отправлен доверенной третьей стороне I. Верификатор V получит все значения полинома Z для каждого a из I и затем проверит соответственно.

Давайте рассмотрим определение в статье:

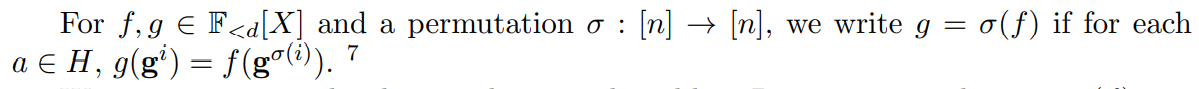
На основе определения: многочлены f и g имеют один и тот же набор значений в зависимости от диапазона [n]. Мы рассмотрим конкретную часть протокола в сочетании с тремя пунктами, описанными выше.

Примечание: f и g на рис. 4 соответствуют f на рис. 3. Другими словами, f и g — одни и те же многочлены. Пока это множество одного и того же значения, это может быть не один и тот же многочлен. Рисунок 3 — это частный случай.

（2）Проверка перестановки полиномов

Доказать, что для конкретных многочленов f, g существуют две точки x, y, где f(x) = g(y). Есть два различия по сравнению с (1):

1. Многочленов несколько.

1. Связь между х и у не является обязательной; он может быть равным или нет.

На основе раздела (1) мы сначала рассмотрим связанные определения:

Согласно определению, это проверка перестановки между двумя полиномами. Из подчеркнутой части видно:

1. Два набора многочленов по-прежнему имеют одинаковые значения.

1. Чтобы различать многочлены в множестве, необходимо различать индекс независимой переменной.

Следовательно, если есть два полинома f и g, и вы хотите доказать f(x) = g(y), согласно приведенному выше описанию, вы можете вычесть {f1,f2} = {f,g} = {g1, g2}, что также обеспечивает справедливость первого пункта выше.

Рассмотрим конкретные принципы:

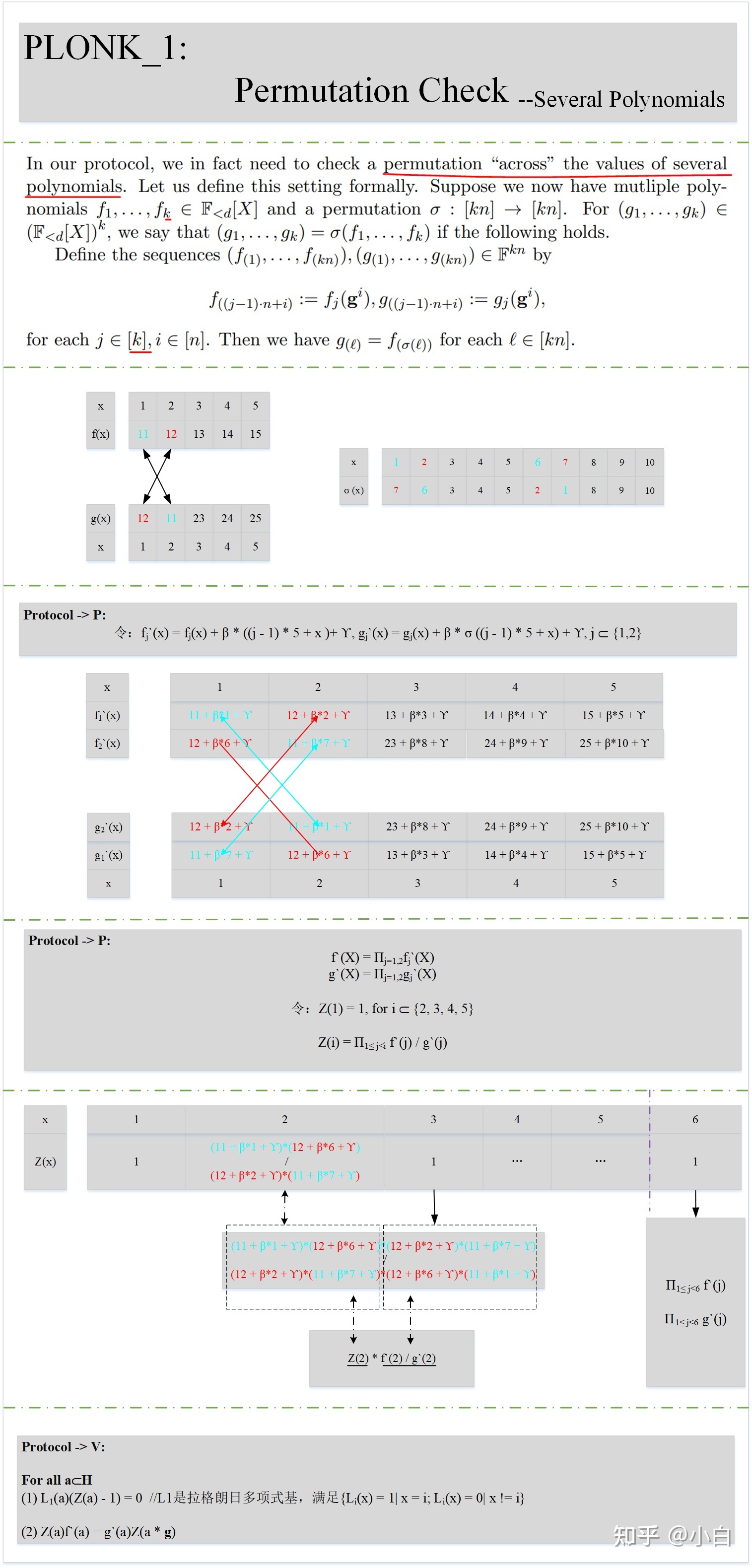
По сравнению с разделом (1) рабочая нагрузка доказывающего P увеличилась, а рабочая нагрузка верификатора V осталась прежней. В соответствии с приведенным выше описанием математические принципы также могут быть легко поняты.

Примечание. На самом деле мы постепенно перешли к основной части алгоритма PLONK. Как мы упоминали ранее, выполнимость схемы — это не только отношение ограничения внутри элемента, но также и отношение ограничения между элементами.

Например, вход x является одновременно левым входом вентиля умножения и правым входом другого вентиля умножения. Следовательно, необходимо доказать L(m)=R(n), что называется проверкой перестановок между многочленами.

На рисунке ниже представлены детали протокола в документе:

Вывод

В этой статье обсуждались две критически важные темы PLONK: проектирование схемы и процесс проверки ограничения копирования. Мы проанализируем действительность ограничения ворот и подробности протокола в следующей статье.