
Почему эгоистичная добыча более опасна, чем вы думаете
2 июля 2025 г.Таблица ссылок
Аннотация и 1. Введение
1.1 Связанная работа
Предварительные
2.1 Системная модель
2.2 Цель эгоистичной добычи
2.3 Процессы принятия решений Маркова
Эгоистичная горнодобывающая атака
3.1 Обзор
3.2 Формальная модель
3.3 Формальный анализ
3.4 Ключевые функции и ограничения
Экспериментальная оценка
Заключение, подтверждение и ссылки
A. NAS Mining Цели
B. Системы эффективных доказательств
C. Доказательство теоремы 3.1
3.2 Формальная модель
Теперь мы официально моделируем нашу эгоистичную горнодобывающую атаку как MDP. Напомним, что MDP M = (𝑆, 𝐴, 𝑃, 𝑠0) - это упорядоченный кортеж, где 𝑆 - конечный набор состояний, 𝐴 - это конечный набор действий, перегруженных для указания для каждого состояния 𝑠 ∈ 𝑆 Набор доступных действий 𝐴 (𝑠) ⊆ 𝐴, 𝑃: × → d (𝑆 𝑆 𝑆 𝑆 𝑆 𝑆 𝑆 → → → → → → → → → → → → → → → → → состояние. Следовательно, чтобы официально моделировать нашу атаку как MDP, нам нужно определить каждый из этих четырех объектов.
Параметры модели.Наша модель MDP использует в качестве основы модель системы, которую мы определили в разделе 2.2. Таким образом, это параметризовано параметрами 𝑝 и 𝛾, но также и тремя дополнительными параметрами, специфичными для самого эгоистичной майнинговой атаки. Мы используем n для обозначения набора всех положительных целых чисел:
• Относительный ресурс противника.𝑝 ∈ [0, 1] обозначает долю ресурсов в блокчейне, принадлежащем противнику.
• Переключение вероятностиПолем 𝛾 ∈ [0, 1] обозначает вероятность того, что честный шахтер переключится на недавно выявленную состязательную цепь, которая имеет такую же длину, что и основная цепь.
• Глубина атаки.𝑑 ∈ N обозначает глубину атаки противника на цепь, то есть количество последних блоков на основной цепи, на которой шахты противника горны.
• Номер разбиванияПолем 𝑓 ∈ N обозначает количество частных вилок, которые противник создает в каждом из последних 𝑑 публичных блоков.
• Максимальная длина вилки.𝑙 ∈ N обозначает максимальную длину частной вилки. Введение этого параметра гарантирует, что наша модель MDP состоит из конечных состояний, что необходимо, поскольку существующие решатели MDP среднего платежа применимы к MDP конечных состояний [18, 20]. Мы обсуждаем последствия этого в разделе 3.4.
Определение MDPПолем Мы определяем MDP M = (𝑆, 𝐴, 𝑃, 𝑠0) следующим образом:
• ГосударстваПолем Пространство состояния определяется через
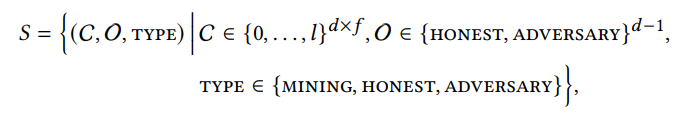
то есть каждое состояние определяется как тройной (c, o, тип), где C определяет текущую конфигурацию блокчейна (то есть топология) до глубины 𝑑, o указывает, кто владеет каждым блоком в основной цепочке до глубины 𝑑 (честные шахтеры или противник), и тип указывает, являются ли партии по -прежнему добывать или какая -то сторона, у него есть новый блок и должен добавить его в блок. В частности:
-Для каждого 1 ≤ 𝑖 ≤ 𝑑 и 1 ≤ 𝑗 ≤ 𝑓 мы используем C [𝑖, 𝑗], чтобы обозначать длину 𝑗-т-ту частную вилку, добываемую противником на глубине 𝑖 блока на главной цепи. Каждая частная вилка имеет большую часть 𝑙, поэтому мы навязываем, что каждый 𝐶 [𝑖, 𝑗] ∈ {0 ,. Полем Полем , 𝑙}.
- Для каждого 1 ≤ 𝑖 <𝑑 мы используем O [𝑖], чтобы обозначать, кто владеет блоком на глубине 𝑖 в основной цепи. В частности, o [𝑖] = честно, если блок принадлежит честным шахтерам и O [𝑖] = противник, если блок принадлежит противнику.
- Наконец, Type Указывает, является ли новый блок, который должен быть добавлен в блокчейн, все еще добывается, и в этом случае мы устанавливаем Type = Mining, или если какая -то сторона сгенерировала доказательство и добавит новый блок, в этом случае мы устанавливаем Type = честный и тип = противник соответственно.
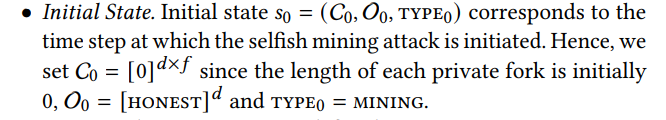
• ДействияПолем Пространство действий определяется через
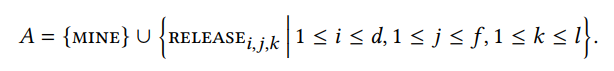
Интуитивно предписывает, что противник не должен выпускать какие -либо частные вилки и просто продолжать добывать новые блоки. С другой стороны, выпуск 𝑗, 𝑘 предписывает, что противник должен опубликовать первые 𝑘 блоки 𝑗-th Private Fork, добываемой на блоке на глубине 𝑖 в главной цепи. Набор доступных действий в каждом состоянии MDP 𝑠 = (C, O, тип) определяется следующим образом:
- Если тип = добыча, то 𝐴 (𝑠) = {mine}.
- if type ∈ {честно, противник}, то 𝐴 (𝑠) = {mine} ∪ {release𝑖, 𝑗, 𝑘 | 𝑘 ≤ C [𝑖, 𝑗]}, где условие 𝑘 ≤ c [𝑖, 𝑗] просто гарантирует, что длина опубликованной части частной вилки не может превышать общую длину частного вилка.
• Функция переходаПолем Наконец, мы определяем функцию перехода 𝑃: 𝑆 × 𝐴 → D (𝑆). Пусть 𝑠 = (c, o, тип) и 𝑎 ∈ 𝐴 (𝑠) быть действием, доступным в 𝑠:
- Если тип = добыча, то мы должны иметь 𝑎 = моя в качестве единственного доступного действия. Следующее состояние в MDP выбран вероятно, в зависимости от того, кто сводит следующий блок и где. Напомним, что честные шахтеры владеют 1 -𝑝 доли ресурсов в блокчейне и добывают только в основной цепи, тогда как противник владеет 𝑝 доли ресурсов, но в максимум 𝑑 · · · · · 𝑓 𝑓 𝑓 𝑓 𝑓 𝑓 𝑓 𝑓 𝑓 𝑓 Обратите внимание, что противник будет одновременно добывать поверх каждого частного вилка, начиная с общественных блоков до глубины 𝑑 в основной цепи, а также поверх каждого общественного блока до глубины 𝑑, в которой были инициированы не все частные работы. Следовательно:

-if type = честный и 𝑎 = release𝑖, 𝑗, 𝑘 𝑘, тогда противник публикует первые 𝑘 блоки 𝑗-th Private Fork, добываемой на блоке на глубине 𝑖 в главной цепи. Следовательно, следующее состояние MDP определяется цепью, которая принимается в качестве основной цепи честными шахтерами. Если недавно опубликованная вилка строго длиннее, чем основная цепочка, честные шахтеры принимают ее как новую основную цепь с вероятностью 1. В противном случае, если основная цепь и опубликованная вилка имеют одинаковую длину, то происходит «раса» между цепями, и опубликованная вилка становится основной цепью с вероятностью переключения 𝛾. Следовательно:

где C ′ и C ′ ′ определяются как предыдущий случай. Обратите внимание, что если опубликованная вилка и основная цепь имеют одинаковую длину, гонка не может произойти, поскольку последний блок был добыт противником, и для всех шахтеров было прошло достаточно времени, чтобы получить общественную цепь
Авторы:
(1) Krishnendu Chatterjee, IST Австрия, Австрия (Krishnendu.chatterjee@ist.ac.at);
(2) Амирали Эбрагимзаде, Технологический университет Шарифа, Иран (ebrahimzadeh.amirali@gmail.com);
(3) Мехрдад Карраби, Ист Австрия, Австрия (Mehrdad.karrabi@ist.ac.at);
(4) Krzysztof Pietrzak, IST Австрия, Австрия (Krzysztof.pietrzak@ist.ac.at);
(5) Мишель Йео, Национальный университет Сингапура, Сингапур (mxyeo@nus.edu.sg);
(6) ðorđe žikelić, Сингапурский университет управления, Сингапур (dzikelic@smu.edu.sg).
Эта статья есть
Оригинал
