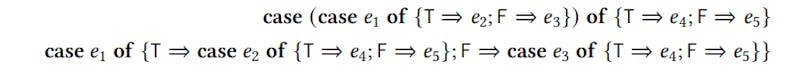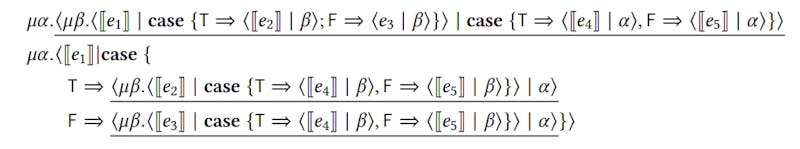Почему писатели компиляторов заботятся о случаях
9 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
5.3 LET-связы
Строительство метки в веселом переводится в ядро. Кроме того, при рассмотрении правила печати для метки 𝛼 {𝑡} в разделе 4.1 мы видим, что оно напрямую соответствует печати 𝜇-связывания с меткой 𝛼, которая является связанным ковриным. Аналогичным образом, связывание let переводится как 𝜇 𝜇-связывающую и печатающую let-связующую в веселом Таким образом, этикетки и лепные связки являются двойными друг для друга, одинаково 𝜇 и 𝜇 𝜇. Двойственность может быть распространена на другие операторы управления, такие как Call/CC.
Как выясняется, конструкция метки очень тесно связана с Call/CC. На самом деле есть только два различия. Во -первых, метка 𝛼 {𝑡} имеет связующее 𝛼 для продолжения, встроенного в конструкцию, так же, как изменение Call/CC с именем let/cc (который Рейнольдс [1972] назвал Escape). Второе и более важное отличие состоит в том, что вызов продолжения, захваченного меткой 𝛼 {𝑡}, происходит через явную языковую конструкцию (𝑡; 𝛼). Это позволяет легко дать перевод в ядро, так как мы можем просто вставить еще одну 𝜇-связующую, чтобы отказаться от оставшегося продолжения в том месте, где вызывается захваченное продолжение. Напротив, с помощью Call/CC и let/cc продолжение применяется так же, как и нормальная функция, что делает необходимым переопределить переменную, сдерживаемое продолжение при переводе с ядром. Это скрывает двойственность, чтобы позволить связывания, что настолько очевидно для лейбла и гомо.
Чтобы увидеть это, вот перевод let/cc 𝑘 𝑡 на ядро
[let/cc 𝑘 𝑡] ≔ 𝜇𝛼.⟨cocase {ap (𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩} | 𝜇𝑘. ˜ ⟨[𝑡] | 𝛼⟩⟩
Суть перевода по -прежнему заключается в том, что текущее продолжение захватывается внешним 𝜇 и связано с 𝛼. Но теперь мы также должны преобразовать это 𝛼 в функцию (здесь коказ), которая отбрасывает его контекст (здесь, связанный с 𝛽) и связывать эту функцию с 𝑘, которая выполняется с использованием 𝜇𝜇. Для Call/CC двойственность еще более скрыта, так как там переплет для продолжения скрыт в функции, к которой применяется Call/CC. Для перевода эта функция должна быть применена к вышеуказанной коказе и захваченному продолжению 𝛼, что приводит к следующему термину (см. Также [Miquey 2019]).
[Call/CC 𝑓] ≔ 𝜇𝛼.⟨ [𝑓] | AP (Cocase {ap (𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩}, 𝛼)⟩
Другие операторы управления для неосновных продолжений могут быть переведены аналогичным образом. Например, рассмотрим Felelisen C [Felleisen et al. 1987]. Разница в вызове/CC состоит в том, что C отказывается от текущего продолжения, если оно не используется где-то в термине C, к которому применяется, тогда как Call/CC оставляет его на месте и, таким образом, ведет себя как не-операционная, если захваченное продолжение никогда не вызывается. Единственное изменение, которое необходимо внести в перевод в ядро, заключается в том, что продолжение верхнего уровня должно использоваться для внешнего разреза вместо использования захваченного продолжения. Это наиболее легко видно для вариации C, который имеет связующее для продолжения, встроенного в оператор, и где вызов продолжения является явным, аналогично метке/GOTO. Называя эту вариационную метку, мы получаем следующий перевод
[labelc 𝛼 {𝑡}] ≔ 𝜇𝛼.⟨ [𝑡] | ⋆⟩
Здесь двойственность, чтобы позволить связываниям, снова очевидна. Перевод для самого C затем получен таким же образом, как и для Call/CC
[C 𝑓] ≔ 𝜇𝛼.⟨ [𝑓] | AP (Cocase {ap (𝑥, 𝛽) ⇒ ⟨𝑥 | 𝛼⟩}, ⋆)⟩
5.4 Трансформация случая
Одним из важных трансформаций в функциональных компиляторах является преобразование случая. Maurer et al. [2017] приведите следующий пример этого преобразования. Термин
если (если𝑒1затем𝑒2еще𝑒3)затем𝑒4еще𝑒5
может быть заменен на термин
если𝑒1затем (если𝑒2затем𝑒4еще𝑒5)еще (если𝑒3затем𝑒4еще𝑒5).
Логики называют такими видами трансформаций коммутативные конверсии, и они играют важную роль в изучении последовательного исчисления. Но как Maurer et al. [2017] Покажите, они также важны для писателей -компиляторов, которые хотят генерировать эффективный код.
В 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus конверсии не должны осуществляться в качестве специального прохода компилятора. Они выпадают бесплатно в качестве особого случая 𝜇-восстановления! Давайте проиллюстрируем этот момент, переведя пример Маурера и др. В 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus. Во-первых, давайте переведем два примера, используя синтаксис сопоставления шаблонов:
! [] (Данные: Image/SVG+XML,%3CSVG%20xmlns =%27http: //www.w3.org/2000/svg%27%20 Версия =%271,1%27%20width =%27800%27%20Height =%2761,38513513513513%27/%3E)
Давайте теперь переведем эти два термина в 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus:
! [] (Данные: Image/SVG+XML,%3CSVG%20xmlns =%27http: //www.w3.org/2000/svg%27%20 Версия =%271,1%27%20width =%27800%27%20Height =%27128,48765432098767%27/%3e)
Мы можем видеть, что, просто уменьшая все подчеркнутые RedExes, мы уменьшаем оба этих примера до одного и того же термина.
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал