Почему арифметика на функциональных языках требует последовательного исчисления
7 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
2 Перевод к последовательному исчислению
В этом разделе мы вводим удовольствие, ориентированный на выражение языка функционального программирования, а также его перевод в ядро промежуточного языка на основе последовательности. Мы представляем как языки, так и функцию перевода [ -] в нескольких шагах, начиная с арифметических выражений и добавляя больше функций в более поздних подразделах. Мы откладываем правила набора обоих языков до раздела 4.
2.1 Арифметические выражения
Мы начнем с арифметических выражений, которые состоят из переменных, целочисленных литералов, бинарных операторов и IFZ, условного выражения, которое проверяет, равен ли его первый аргумент. Синтаксис арифметических выражений для развлечения и ядра приведен в определении 2.1.

В развлечении есть только одна синтаксическая категория: термины. Этими терминами могут быть переменные 𝑥, литералы ⌜𝑛⌝, бинарные операторы 𝑡 + 𝑡, 𝑡 ∗ 𝑡 и 𝑡 - 𝑡 или условное IFZ (𝑡, 𝑡0, 𝑡1). Это условное оценивает до 𝑡0, если 𝑡 оценивает до ⌜0⌝, или и в противном случае. В отличие от этой единственной категории, Core использует три различные синтаксические категории: производители 𝑝, потребители 𝑐 и операторы 𝑠. Эти категории непосредственно унаследованы от 𝜆𝜇𝜇-калькулуса, и важно понимать их различия:
Производители все строят вОсновнойкоторый конструирует или создает элемент какого -либо типа, принадлежит к синтаксической категории производителей. Другими словами, производители соответствуют «формам введения» или «термины доказательства» и каждому термину языкаВесельепереводится на продюсера вОсновнойПолем
ПотребителиПотребители, вероятно, менее интуитивно понятны, чем производители, поскольку они не соответствуют непосредственному термину языкаВесельеПолем Основная идея состоит в том, что если у некоторых потребителей есть тип 𝜏, то 𝑐 потребляет или разрушает производителя типа 𝜏. Если вы сталкивались с контекстами или продолжениями оценки, то полезно думать о потребителях типа 𝜏 как о продолжениях или контекстах оценки для производителя типа 𝜏. И если вы знакомы с корреспонденцией Curry-Howard, то вы можете думать о потребителях как о опровержении или прямых доказательствах того, что предложение является ложным.
ЗаявленияЗаявления - это ингредиент, который делает вычисление происходить; Без утверждений у нас были бы только статические объекты без какого -либо динамического поведения. Вот не эксплуатационный список примеров для утверждений: каждое действие ввода-навода, которое считывает или печатает на консоли или файл, должно быть представлено в качестве оператора вОсновнойПолем Расчеты по примитивным типам, таким как целые числа машин, должны быть операторами. Наконец, все, что является Redex на языке, основанном на выражении выражения, также должно соответствовать утверждению вОсновнойПолем Поскольку сами заявления вычисляют только и не возвращают ничего, у них нет типа.
После этих общих замечаний давайте рассмотрим, как арифметические выражения представлены в ядре языка. Переменные 𝑥 и литералы ⌜𝑛⌝ оба принадлежат к категории производителей, но бинарные операторы представлены в виде утверждений ⊙ (𝑝1, 𝑝2; 𝑐). Во -первых, давайте объясним, почему они представлены в качестве заявлений вместо производителей. Идея состоит в том, что бинарный оператор на примитивных целых числах должен оцениваться непосредственно с помощью арифметической логики (ALU) базовой машины. И любая операция, которая непосредственно вызывает машину, должна принадлежать к той же синтаксической категории, что и печатная или другая инструкция IO: операторы. Машина не возвращает результат; Скорее, он считывает входы из регистров и предоставляет результат доступным в регистре для дальнейшего вычисления. Это также отражено во втором удивительном аспекте: у оператора есть три вместо двух аргументов. Два производителя 𝑝1 и 𝑝2 соответствуют обычным аргументам, но третий аргумент потребителя 𝑐 говорит, что должно произойти с результатом после оценки бинарного оператора. Это похоже на спорный аргумент функции в стиле продолжения. Бинарные операторы ⊙ (𝑝1, 𝑝2; 𝑐) также отображают синтаксическую конвенцию, которую мы используем: всякий раз, когда в некоторых конструкциях есть аргументы различных синтаксических категорий, мы используем полуколон вместо запятой для их разделения.
Мы можем сразу же увидеть, что результат J𝑝1 + 𝑝2k должен содержать утверждение + ([𝑝1] [𝑝2];?), Но нам все еще нужно выяснить, какой потребитель подключиться к месту третьего аргумента и как преобразовать это утверждение в производителя. Мы можем сделать это с помощью Abstraction in Core, которое превращает заявление в производителя при привязке ковариации 𝛼: 𝜇𝛼. + ([𝑝1], [𝑝2]; 𝛼).
Заявление IFZ работает аналогично бинарным операторам: это вычисление, которое проверяет, является ли производитель 𝑝 равен нулю, а затем продолжается с одной из двух его ветвей. Эти ветви также являются операторами, указывающими, какие вычисления выполнять после оценки условия. На языке развлечения эти две ветви были терминами, поэтому нам теперь нужно найти способ преобразовать двух продюсеров в два утверждения. Мы можем сделать это, используя разрез ⟨𝑝 | 𝑐⟩ Что объединяет производителя и потребителя того же типа, чтобы получить утверждение в каждой ветви: ifz ([𝑡1], ⟨[𝑡2] |?⟩, ⟨[𝑡3] |?⟩). Затем мы можем использовать одну и ту же ковариацию 𝛼 в обоих утверждениях, чтобы представлять тот факт, что мы хотим, чтобы результат в любой филиале вернулся к одной и той же точке в программе; Мы снова используем окружающее 𝜇-связывание, чтобы связать эту ковариацию: 𝜇𝛼.ifz ([𝑡1], ⟨[𝑡2] | 𝛼⟩, ⟨[𝑡3] | 𝛼⟩).
Давайте теперь посмотрим, как оцениваются арифметические выражения. Определение 2.2 вводит синтаксис значений и ковалеев и показывает, как уменьшить немедленные Redexes. Мы используем простую синтаксическую конвенцию здесь: метавария для значения терминов - 𝔱, записаны значения производителей 𝑝, а коваленты, которые соответствуют потребителям, написаны 𝔠. Мы используем символ ⊲ для уменьшения как веселья, так и для ядра (и записываем ⊲ ∗, когда выполняются несколько шагов одновременно).

Значения и оценка Redexes в веселье просты, единственный примечательный аспект заключается в том, что два правила для IFZ (·, 𝑡1, 𝑡2) не требуют 𝑡1 и 𝑡2, чтобы быть значениями. Таким образом, давайте продолжим обсуждение языкового ядра.
Первым интересным аспектом языкового ядра является то, что существуют как ценности, так и коваленты. Это может быть объяснено той ролью, которую значения играют в оперативной семантике: они указывают подмножество терминов, которые нам разрешают заменить переменную. И поскольку у нас есть обе переменные, которые соответствуют производителям и ковариации, которые стоят за потребителей, нам нужны как значения, так и коваленты в качестве соответствующих подмножеств, которые нам разрешают заменить переменную или коварируемую.
Второй интересный аспект языкового ядра заключается в том, что только заявления уменьшаются, а не производители или потребители. Это подтверждает наше замечание сверху, что это утверждения, которые вводят динамизм в язык за счет вычислений. Это также способствует ощущению, что снижение языка близко к оценке абстрактной машины и что утверждения ядра соответствуют состояниям такой абстрактной машины.
Мы все еще сталкиваемся с небольшой проблемой, когда хотим показать, что термин веселья оценивается с тем же результатом, что и его перевод в ядро: мы указали только сокращение заявлений, но не для производителей. Мы можем легко решить эту проблему, внедрив специальную коврискую ⋆, которая действует как «верхний» потребителя оценки. Использование ⋆ мы можем затем оценить утверждение ⟨[𝑡] | ⋆⟩ вместо производителя [𝑡].
Пример 2.1.Рассмотрим два термина ⌜2⌝ ∗ ⌜3⌝ и ifz (⌜2⌝, ⌜5⌝, ⌜10⌝) развлечения. Их соответствующие переводы в ядро - 𝜇𝛼. ∗ (⌜2⌝, ⌜3⌝; 𝛼) и 𝜇𝛼.ifz (⌜2⌝, ⟨⌜5⌝ | 𝛼⟩, ⟨⌜10⌝ | 𝛼⟩). Когда мы обертываем их в заявление, используя продолжение верхнего уровня ⋆, мы наблюдаем следующую оценку:
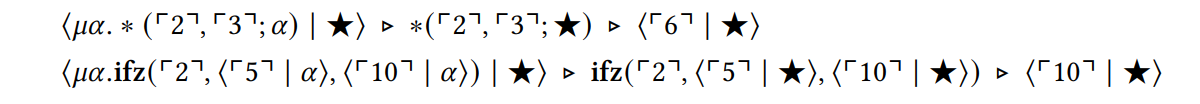
Мы успешно оценили первый термин до результата ⌜6⌝ и второй член к результату ⌜10⌝.
Далее мы часто пропускаем первый этап восстановления в примерах, таким образом, молча заменяя ковариацию, связанную самой внешней 𝜇-связывающей с потребителем верхнего уровня ⋆.
Вот большая проблема, с которой мы еще не решались. Правила оценки в настоящем разделе не позволяют оценивать вложенные выражения, такие как (⌜2⌝ ∗ ⌜4⌝) + ⌜5⌝ в веселье или его перевод 𝜇𝛼. + (𝜇𝛽. ∗ (⌜2⌝, ⌜4⌝; 𝛽), ⌜5⌝; 𝛼) в ядре. Мы обсудим эту проблему и ее решение более подробно в разделе 3.
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал
