
Что последовательное исчисление учит нас о вычислении
9 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
А отношение к последовательному исчислению
В основной части статьи мы представили 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus без каких-либо ссылок на последовательное исчисление, потому что мы думаем, что не важно понять последнее, чтобы понять первое. В этом приложении мы предоставляем детали, которые помогают установить соединение между логическим исчислением и терминкой системы чистым. Мы обсуждаем только очень простое последовательное исчисление, которое содержит два логических соединений: два соединения 𝐴 𝐵 𝐵 𝐵 𝐵 𝐴 & 𝐵, которые соответствуют строгим и ленивым парам, которые мы видели в ядре. Мы используем 𝑋 для пропозициональных переменных.
𝐴, 𝐵 f 𝑋 | 𝐴 ⊗ 𝐵 | 𝐴 & 𝐵
В (классическом) последовательном исчислении как предпосылок, так и заключения правила вывода состоят из последовательности γ Δ. Как γ, так и δ являются многоселами формул; То есть важно, как часто формула происходит слева или правой, но не в том, в каком порядке возникают формулы. В последовательном исчислении у нас есть только правила введения. Это означает, что логически сложная формула 𝐴 𝐵 𝐵 𝐵 𝐵 𝐴 & 𝐵 происходит только в заключении правил, которые его определяют, а не в одном из помещений. Каждое соединение поставляется с набором правил, которые вводят соединение слева и справа от турникета. В нашем случае правила выглядят так:
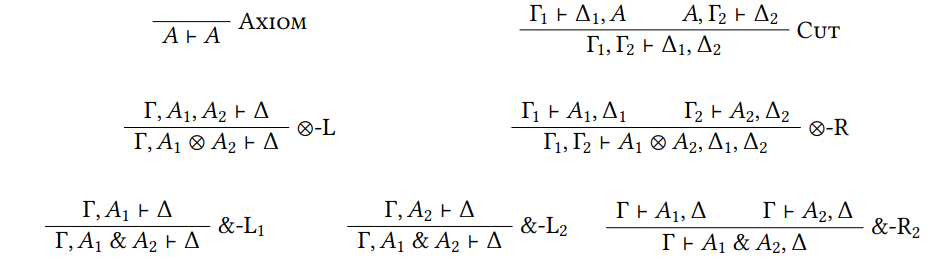
The rule Cut is the only rule which destroys the so-called subformula property. This property says that every formula which occurs anywhere in a derivation is a subformula of a formula occurring in the conclusion of the derivation. Proof theorists therefore try to show that we can eliminate the cuts; if every sequent which can be derived using the Cut rule can also be derived without using it, we say that the calculus enjoys the cut-elimination property. The Curry-Howard correspondence for the sequent calculus relates this cut-elimination procedure to the computations that we have seen in the paper.
Первый шаг от последовательного исчисления к 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus состоит в маркировке, не более одной из формул в каждой из последовательности как активных. Мы отмечаем формулу как активную, заключая ее в пару скобков. Это дает две версии аксиомы правила, в которой мы отмечаем формулу слева и одна, где мы отмечаем формулу справа. Если мы хотим перевести каждый вывод, используя исходные правила на вывод в новом варианте, мы также должны добавить специальные правила, которые активируют и деактивируют формулы как слева, так и справа. Это дает следующий новый набор правил:

B Правила печатания для развлечения
Учитывая термин 𝑡, среда γ и программа 𝑃, если 𝑡 имеет тип 𝜏 в среде γ и программа 𝑃, мы пишем γ ⊢𝑃 𝑡: 𝜏. Поскольку 𝑃 используется только для печати вызовов в определениях верхнего уровня (вызов правила), мы обычно оставляем это подразумевающим в правилах набора. Чтобы убедиться, что программы 𝑃 хорошо сформированы, у нас есть дополнительные правила проверки для программ ∅-ok и p-ok. Если программа хорошо сформирована, мы пишем ⊢ 𝑃 OK.


C Оперативная семантика лейбла/goto
Полная эксплуатационная семантика для конструкции лейбла/goto по сути такая же, как и для let/cc. Чтобы сделать это точным, мы продвигаем контексты оценки до значений времени выполнения
Сначала повторяем определение 3.1 контекстов оценки с одним изменением: метка 𝛼 {𝐸} не является контекстом оценки. Мы уменьшаем этикетку, как только он попадет в оценку.
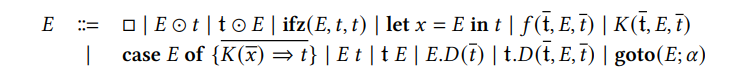
Теперь мы добавляем их в качестве другой формы стоимости
𝔱 f. Полем Полем | 𝐸
Обратите внимание, что эти значения существуют только во время выполнения, то есть они не могут появиться в выражениях до начала оценки. Они печатаются как потребители, что означает, что они являются единственными значениями с типом потребителя. Это гарантирует, что мы можем заменить их на ковариации. Их набор может быть захвачен следующим правилом.
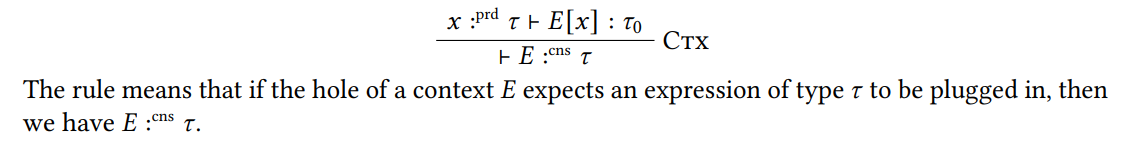
Теперь мы можем дать правила оценки для лейбла и goto:
𝐸 [метка 𝛼 {𝑡}] ⊲ 𝐸 [𝑡 [𝐸/𝛼]] 𝐸 ′ [goto (𝔱; 𝐸)] ⊲ 𝐸 [𝔱]

Правило для GOTO также является причиной, по которой теорема сильного сохранения не сразу же (см. Обсуждение в разделе 4.3). Проблема заключается в том, что из этого правила и данных правил печати для развлечения не сразу же, что контексты оценки 𝐸 ′ и 𝐸 дают термин одного и того же типа при заполнении их отверстий, так что общий тип термина не может быть сохранен. Но это на самом деле не может произойти, потому что все другие правила сокращения сохраняют общий тип, и, следовательно, все контексты оценки, которые укрепляются правилом для метки, должны дать термин того же общего типа, когда их отверстия заполнены. Следовательно, также правило GOTO является сохранением типов. Это может быть сделано точным путем явного отслеживания общего типа в системе типов (см., Например, раздел 6 в [Wright and Felleisen 1994]).
Ссылки
Андреас Абель, Бриджит Пинтека, Дэвид Тибодо и Антон Сетцер. 2013. Copatterns: программирование бесконечных структур с помощью наблюдений. В материалах 40-го ежегодного симпозиума ACM Sigplan-SIGACT по принципам языков программирования (Рим, Италия) (POPL ’13). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 27–38. https://doi.org/ 10.1145/2480359.2429075
Жан-Марк Андреоли. 1992. Логическое программирование с фокусирующими доказательствами в линейной логике. Журнал логики и вычислений 2 (1992), 297–347. Выпуск 3. https://doi.org/10.1093/logcom/2.3.297
Джонатан Иммануэль Брахтхаузер, Филипп Шустер и Клаус Остерманн. 2020. Эффекты как возможности: обработчики эффекта и легкий полиморфизм эффекта. Прокурор Программа ACM. Ланг 4, OOPSLA, статья 126 (ноябрь 2020 г.), 30 страниц. https: //doi.org/10.1145/3428194
Уильям Р. Кук. 2009. О понимании абстракции данных, повторно. В материалах конференции по объектно-ориентированному программированию, системам, языкам и приложениям: далее! Эссе (Орландо). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 557–572. https://doi.org/10.1145/1640089.1640133
Пьер-Луи Кюриен и Хьюго Хербелин. 2000. Двойственность вычислений. В материалах Пятой международной конференции ACM Sigplan по функциональному программированию (ICFP ’00). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 233–243. https://doi.org/10.1145/357766.351262
Пьер-Луи Кюриен и Гийом Мунк-Макканнини. 2010. Двойственность вычислений находится в центре внимания. В теоретической информатике Кристиан С. Калуда и Владимиро Сассоне (ред.). Springer Berlin Heidelberg, Берлин, Гейдельберг, 165–181.
Пол Даунен и Зена М. Ариола. 2014. Двойственность строительства. В материалах 23 -го Европейского симпозиума по языкам и системам программирования - Том 8410 (ESOP ’14). Springer, Berlin, Heidelberg, 249–269. https: //doi.org/10.1007/978-3-642-54833-8_14
Пол Даунен и Зена М. Ариола. 2018a. За пределами полярности: к многодисциплинарному промежуточному языку с обменом. В 27 -й ежегодной конференции EACSL по логике компьютерных наук (CSL 2018) (Международное разбирательство Leibniz Informatics (Lipics), том 119), Dan Ghica и Achim Jung (ред.). Schloss Dagstuhl - Leibniz -Zentrum für Informatik, Dagstuhl, Германия, 21: 1–21: 23. https://doi.org/10.4230/lipics.csl.2018.21
Пол Даунен и Зена М. Ариола. 2018b. Учебник по вычислительной классической логике и последовательному исчислению. Журнал функционального программирования 28 (2018). https://doi.org/10.1017/S0956796818000023
Пол Даунен и Зена М. Ариола. 2020. Компиляция с классическими соединениями. Логические методы в информатике Том 16, выпуск 3 (август 2020 г.). https://doi.org/10.23638/lmcs-16(3:13)2020
Пол Даунен, Филипп Джонсон-Фрейд и Зена М. Ариола. 2015. Структуры для структурной рекурсии. В материалах 20 -й международной конференции ACM Sigplan по функциональным программированию (Ванкувер, Британская Колумбия, Канада) (ICFP 2015). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 127–139. https://doi.org/10.1145/2784731.2784762
Пол Даунен, Люк Маурер, Зена М Ариола и Саймон Пейтон Джонс. 2016. Последовательный исчисление как промежуточный язык компилятора. В материалах 21 -й Международной конференции ACM SIGPLAN по функциональному программированию. 74–88.
Пол Даунен, Захари Салливан, Зена М. Ариола и Саймон Пейтон Джонс. 2019. Кодата в действии. В европейском симпозиуме по программированию (ESOP ’19). Springer, 119–146. https://doi.org/10.1007/978-3-030-17184-1_5
Матиас Феллеисен. 1987. Размышления о J-операторе Лэндина: частично историческая заметка. Компьютерные языки 12, 3 (1987), 197–207. https://doi.org/10.1016/0096-0551(87)90022-1
Матиас Феллеисен, Даниэль П. Фридман, Юджин Колбекер и Брюс Дуба. 1987. Синтаксическая теория последовательного контроля. Теоретическая информатика 52, 3 (1987), 205–237. https://doi.org/10.1016/0304-3975(87)90109-5
Андреме Филински. 1989. Декларативные продолжения: исследование двойственности в семантике языка программирования. В теории категорий и информатики. Springer-Verlag, Берлин, Гейдельберг, 224–249.
Герхард Дженцен. 1935a. Untersuchungen über Das Logische Schließen. I. Mathematische Zeitschrift 35 (1935), 176–210.
Герхард Дженцен. 1935b. Untersuchungen über Das Logische Schließen. II Mathematische Zeitschrift 39 (1935), 405–431.
Герхард Дженцен. 1969. Собранные документы Герхарда Дженцен. Северо-Голландия издательская компания, Амстердам.
Жан-Ив Жирард. 1987. Линейная логика. Теоретическая информатика 50, 1 (1987), 1–101. https://doi.org/10.1016/0304- 3975 (87) 90045-4
Brian Goetz et al. 2014. JSR 335: Lambda выражения для языка программирования Java. https://jcp.org/en/jsr/detail?id=335
Тимоти Г. Гриффин. 1989. Формул-тип понятия контроля. В материалах 17-го симпозиума ACM Sigplan-SIGACT по принципам языков программирования (Сан-Франциско, Калифорния, США) (Popl ’90). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 47–58. https://doi.org/10.1145/96709.96714
Тацуя Хагино. 1989. Codatatypes в ML. Журнал символических вычислений 8, 6 (1989), 629–650. https://doi.org/10.1016/ S0747-7171 (89) 80065-3
Питер Джон Ландин. 1965. Переписка между Алголом 60 и Церковным Ламбда-нотацией: Часть I. Коммун. ACM 8, 2 (февраль 1965 г.), 89–101. https://doi.org/10.1145/363744.363749
Пол Блейн Леви. 1999. ЗАКЛЮЧИТЕЛЬНОЙ ЗАПОЛНЕНИЯ: Обращающаяся парадигма. В материалах 4 -й Международной конференции по типированным лямбдам Calculi и заявкам (TLCA ’99). Springer-Verlag, Берлин, Гейдельберг, 228–242.
Люк Маурер, Пол Даунен, Зена М. Ариола и Саймон Пейтон Джонс. 2017. Компиляция без продолжения. В материалах 38 -й конференции ACM Sigplan по дизайну и реализации языка программирования (Барселона, Испания) (PLDI 2017). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 482–494. https://doi.org/10.1145/3062341.3062380
Этиен Мики. 2019. Классическое последовательное исчисление с зависимыми типами. ACM Trans. Программа Ланг Система 41, 2, статья 8 (март 2019 г.), 47 страниц. https://doi.org/10.1145/3230625
Гийом Мунк-Макканнони. 2009. Фокализа и классическая реализуемость. В области информатики Logic: 23 -й международный семинар, CSL 2009, 18 -я ежегодная конференция EACSL (Coimbra, Portugal) (CSL ’09), Эрих Градель и Рейнхард Кале (ред.). Springer, Berlin, Heidelberg, 409–423. https://doi.org/10.1007/978-3-642-04027-6_30
Гийом Мунк-Макканнони. 2013. Синтаксис и модели неассоциативного состава программ и доказательств. Ph. D. Диссертация. Univ. ПАРИЖ ДИДЕРОТ.
Сара Негри и Ян фон Платон. 2001. Теория структурных доказательств. Издательство Кембриджского университета. https://doi.org/10.1017/ CBO9780511527340
Клаус Остерманн, Дэвид Биндер, Инго Скупин, Тим Сюберкруб и Пол Даунен. 2022. Введение и устранение, влево и вправо. Прокурор Программа ACM. Ланг 6, ICFP, статья 106 (2022), 28 страниц. https://doi.org/10.1145/3547637
Мишель Паригот. 1992. 𝜆𝜇-Calculus: алгоритмическая интерпретация классического естественного вычета. В логическом программировании и автоматическом рассуждении Андрей Воронков (ред.). Springer, Berlin, Heidelberg, 190–201.
Джон Чарльз Рейнольдс. 1972. Определение переводчиков для языков программирования высшего порядка. В ACMConf (Бостон). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 717–740. https://doi.org/10.1145/800194.805852
Arnaud Spiwack. 2014. Рассекция Л. (2014). Неопубликованный черновик.
Мортен Хейн Сёренсен и Павес Урзикзин. 2006. Лекции по изоморфизму карри-ховарда. Исследования по логике и основаниям математики, вып. 149. Elsevier.
Хайо Тилекке. 1998. Введение в Ландин «обобщение прыжков и ярлыков». Символ высшего порядка. Вычислительный 11, 2 (сентябрь 1998), 117–123. https://doi.org/10.1023/a:1010060315625
Энн Сьерп Троэльстра и Хельмут Швихтенберг. 2000. Основная теория доказательств, второе издание. Издательство Кембриджского университета.
Филипп Уодлер. 1990. Линейные типы могут изменить мир!. В концепциях и методах программирования. Северная Голландия.
Филипп Уодлер. 2003. Звоните по цене двойной, чтобы позвонить по названию. В материалах восьмой Международной конференции ACM Sigplan по функциональному программированию (Uppsala, Швеция) (ICFP ’03). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 189–201. https://doi.org/10.1145/944705.944723
Филипп Уодлер. 2005. Звоните по цене двойной, чтобы позаботиться по названию-перезагружен. В сроке переписывания и заявлений, 16-я Международная конференция, RTA 2005, NARA, Япония, 19-21 апреля 2005 г., Труды (записки о лекциях в области компьютерных наук, том 3467), Юрген Гисл (ред.). Springer, 185–203. https://doi.org/10.1007/978-3-540-32033-3_15
Эндрю К. Райт и Матиас Феллеисен. 1994. Синтаксический подход к типу звукости. Информация и вычисления 115, 1 (11 1994), 38–94. https://doi.org/10.1006/inco.1994.1093
Ноам Зейлбергер. 2008. О единстве двойственности. Анналы чистой и прикладной логики 153, 1-3 (2008), 66–96. https://doi.org/10. 1016/j.apal.2008.01.001
Ноам Зейлбергер. 2009. Логическая основа заказа оценки и сопоставления моделей. Ph. D. Диссертация. Университет Карнеги Меллона, США. Советник (ы) Пфеннинг, Фрэнк и Ли, Питер.
Йижхоу Чжан, Гвидо Сальванески, Куинн Бейтлол, Барбара Лисков и Эндрю С. Майерс. 2016. Принятие вины за безопасные туннельные исключения. В материалах 37 -й конференции ACM Sigplan по дизайну и реализации языка программирования (Санта -Барбара, Калифорния, США) (PLDI ’16). Ассоциация компьютерной машины, Нью -Йорк, Нью -Йорк, США, 281–295. https://doi.org/10.1145/2908080.2908086
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал
