Математика, стоящая за эгоистичной добычей и распределением наград
2 июля 2025 г.Таблица ссылок
Аннотация и 1. Введение
1.1 Связанная работа
Предварительные
2.1 Системная модель
2.2 Цель эгоистичной добычи
2.3 Процессы принятия решений Маркова
Эгоистичная горнодобывающая атака
3.1 Обзор
3.2 Формальная модель
3.3 Формальный анализ
3.4 Ключевые функции и ограничения
Экспериментальная оценка
Заключение, подтверждение и ссылки
A. NAS Mining Цели
B. Системы эффективных доказательств
C. Доказательство теоремы 3.1
3.3 Формальный анализ
Цель анализаПолем Теперь мы показываем, как вычислить оптимальный ожидаемый относительный доход вместе с состязательной стратегией, достигающей ее в MDP M = (𝑆, 𝐴, 𝑃, 𝑠0), до произвольного параметра точности 𝜖> 0.

быть ожидаемым относительным доходом в соответствии с состязательной стратегией 𝜎, то есть относительное отношение количества блоков, принятых в основной цепочке, принадлежащей противнику и честным шахтерам. Более того, пусть
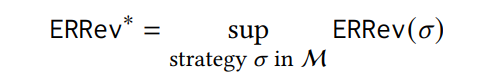
быть оптимальным ожидаемым относительным доходом, который может достичь состязательной стратегии. Учитывая точный параметр 𝜖> 0, наша цель - вычислить

Мы делаем это, определяя класс функций вознаграждения в MDP M и показывая, что для любого значения параметра точности 𝜖> 0 мы можем вычислить вышеперечисленное, решив MDP среднего платежника в отношении функции вознаграждения, принадлежащей этому классу. Наш анализ опирается на понимание [27], которое рассматривало эгоистичную добычу в блокчейнах POW, а также уменьшает рассуждения о ожидаемом относительном доходе для решения MDP средней платежи в отношении соответственно определенных функций вознаграждения. Однако, в отличие от [27], мы рассматриваем эгоистичную добычу в эффективных системах доказательств, в которых противник может добывать на нескольких блоках, что означает, что наш дизайн функций вознаграждения и анализ требует дополнительной помощи.
Определение функции вознагражденияПолем Ключевой задачей в разработке функции вознаграждения является то, что основная цепочка и блоки на ней могут меняться всякий раз, когда противник публикует частную вилку. Следовательно, мы разрабатываем функцию вознаграждения, чтобы понести положительное (соответствующее отрицательное) вознаграждение всякий раз, когда блок, принадлежащий противнику (соответственно честные шахтеры), принимается на глубине, строго больше, чем 𝑑 в главной цепи. Поскольку противник только шахты и публикует частные вилки, добываемые на блоках до глубины 𝑑 в основной цепи, это означает, что блоки за пределами глубины 𝑑гарантированнооставаться на главной цепи.
Формально, для каждого 𝛽 ∈ [0, 1] мы определяем 𝑟𝛽: 𝑆 × 𝐴 × 𝑆 → R, чтобы быть функцией вознаграждения в M, который для каждого тройного состояния состояния (𝑠, 𝑎, 𝑠 ′) назначает вознаграждение:
• 1 - 𝛽, для каждого блока, принадлежащего кпротивникпринято на глубине, превышающую 𝑑 в результате выполнения действия;
• −𝛽, для каждого блока, принадлежащего кчестные шахтерыпринято на глубине, превышающую 𝑑 в результате выполнения действия.

Формальный анализ.Наш формальный анализ основан на следующей теореме. Для ясности экспозиции мы откладываем доказательство теоремы в Приложение c. Для каждого 𝜖> 0 теорема показывает, как связывать оптимальный ожидаемый относительный доход в MDP и 𝜖-оптимальные стратегии с оптимальным средним платом и оптимальными стратегиями в соответствии с функцией вознаграждения 𝑟𝛽 для соответствующего выбранного значения 𝛽.



Авторы:
(1) Krishnendu Chatterjee, IST Австрия, Австрия (Krishnendu.chatterjee@ist.ac.at);
(2) Амирали Эбрагимзаде, Технологический университет Шарифа, Иран (ebrahimzadeh.amirali@gmail.com);
(3) Мехрдад Карраби, Ист Австрия, Австрия (Mehrdad.karrabi@ist.ac.at);
(4) Krzysztof Pietrzak, IST Австрия, Австрия (Krzysztof.pietrzak@ist.ac.at);
(5) Мишель Йео, Национальный университет Сингапура, Сингапур (mxyeo@nus.edu.sg);
(6) ðorđe žikelić, Сингапурский университет управления, Сингапур (dzikelic@smu.edu.sg).
Эта статья есть
Оригинал
