
Основные уравнения, которые могут упростить пейджинг/разбиение на разделы
10 января 2023 г.Изучите математические уравнения разбиения на страницы/разделы и способы их применения в коде JavaScript и .NET C#.
Концепция Paging или Partitioning используется во многих областях. Когда у вас есть набор элементов и вы хотите разделить их поровну между какими-то контейнерами или группами, вы думаете о подкачке или разбиении на разделы, но, возможно, вы еще не распознали это…
Основные цели этой статьи:
- Объясните некоторые математические уравнения, которые облегчат вам реализацию концепции разбиения на страницы или секционирования.
- Предоставьте несколько примеров кода для реализации разбиения по страницам.

Отказ от ответственности
- Если вы ожидаете найти объяснения концепции подкачки в конкретных приложениях, таких как управление памятью операционной системы или файловая система,… значит, вы читаете не ту статью.
- Всякий раз, когда упоминается «Страница» или «Разбивка по страницам», «Раздел» и «Разделение на разделы» быть действительным. Поэтому для краткости я буду использовать «Страница» и «Пейджинг».

Назад к основам
Лучший способ объяснить разбиение на страницы — обратиться к примеру. Предположим, у нас есть коллекция из 10 предметов, любых предметов, может быть, бутылок, карандашей, бананов… всего, что делает вас счастливыми.
Теперь мы хотим разделить эти 10 элементов на группы, каждая из которых содержит 3 элемента.
Если мы сделаем это вручную, элементы будут распределены, как показано на изображении ниже.
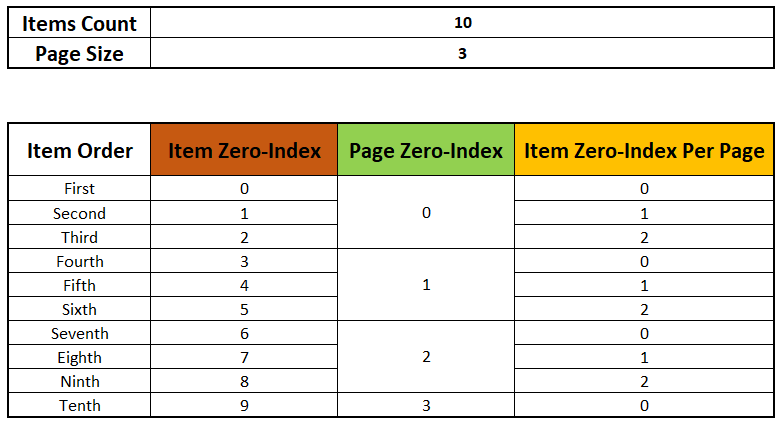
Это было легко, правда?
Давайте объясним, что у нас есть в таблице выше.
- Первый элемент, содержащий 0 в качестве нулевого индекса, будет найден в позиции 0 с нулевым индексом внутри страницы. 0 с нулевым индексом.
- Второй элемент, содержащий 1 в качестве нулевого индекса, будет находиться в позиции 1 с нулевым индексом внутри страницы. 0 с нулевым индексом.
- Третий элемент, содержащий 2 в качестве нулевого индекса, будет находиться в позиции 2 с нулевым индексом внутри страницы. 0 с нулевым индексом.
- Четвертый элемент с нулевым индексом 3 будет находиться в позиции 0 с нулевым индексом внутри страницы. из 1 с нулевым индексом.
- Пятый элемент с нулевым индексом 4 будет находиться в позиции 1 с нулевым индексом внутри страницы. из 2 с нулевым индексом.
- И так далее…
На этот раз вы могли сделать это вручную, так как количество элементов не такое большое, но это не всегда так. Поэтому нам нужно проанализировать приведенный выше пример и придумать некоторые математические формулы.

Формула
Проведя некоторый анализ, мы можем прийти к следующей формуле:

Позволь мне объяснить; когда вы делите нулевой индекс элемента на размер страницы, вы получаете две вещи:
- Результат, представляющий нулевой индекс страницы
- Остаток, представляющий нулевой индекс элемента на странице.
Ты мне не веришь? хорошо, я покажу вам…

Момент истины
Давайте применим формулу к нашему примеру и посмотрим, что получится дальше.
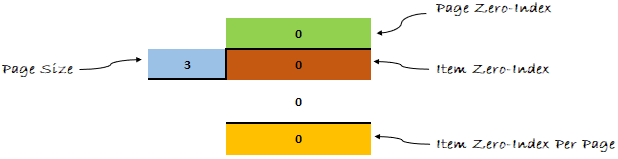
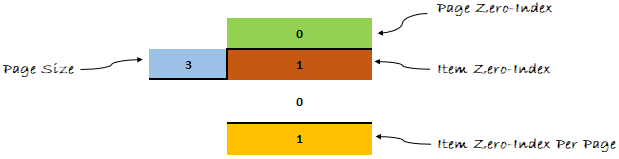
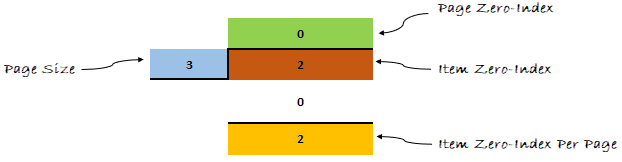
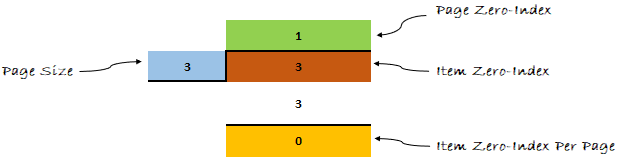
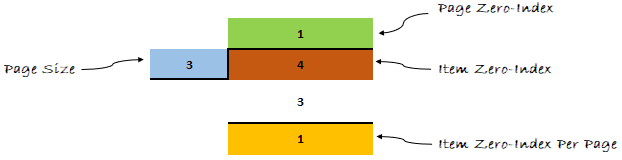
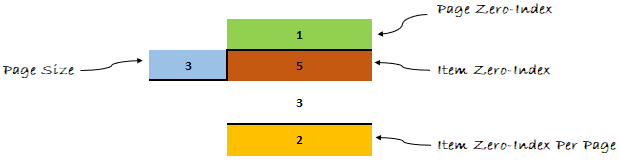
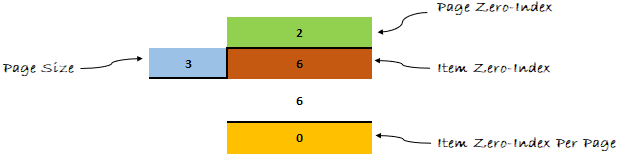
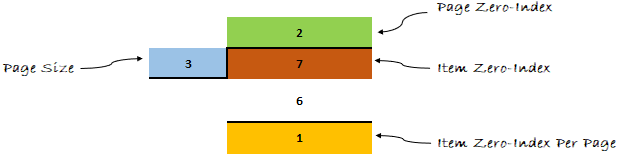
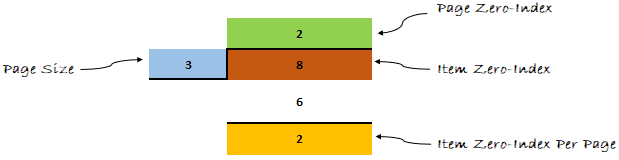
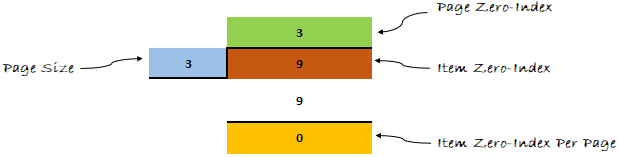
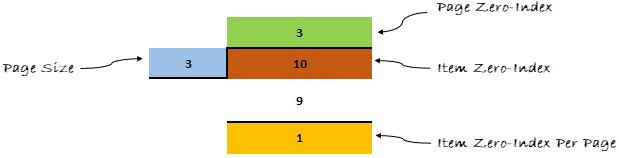
Думаю, теперь ты мне веришь. Формула доказала свою эффективность.

Дальнейший анализ
Доказав формулу, давайте проведем дополнительный анализ.
Формула может быть преобразована в форму ниже:
<цитата>Нулевой индекс элемента = (Нулевой индекс страницы * < em>Размер страницы) + (Нулевой индекс элемента на странице)
Это означает, что если у нас есть значение Нулевой индекс страницы и значение Размер страницы, нам нужно знать Нулевой индекс. > первого элемента и последнего элемента на этой странице, мы можем использовать приведенное выше уравнение следующим образом.
**Первый элемент с нулевым индексом = (Нулевой индекс страницы * Размер страницы) + Минимум (Нулевой индекс элемента на странице) n = (Нулевой индекс страницы * Размер страницы) + 0 n = (Нулевой индекс страницы * Размер страницы)
**Последний элемент с нулевым индексом = (Нулевой индекс страницы * Размер страницы) + Максимум (Нулевой индекс элемента на странице) n = (Нулевой индекс страницы * Размер страницы) + (Размер страницы — 1)
Но обратите внимание: если рассчитанный нулевой индекс последнего элемента больше, чем индекс последнего элемента во всей коллекции, тогда берется меньшее число, которое является индексом последний элемент во всей коллекции.
Опять ты все еще мне не веришь?
Чтобы проверить эти уравнения, давайте применим наш пример:
- На первой странице (нулевой индекс первого элемента = 0 * 3 = 0) и (нулевой индекс последнего элемента = (0 * 3) + (3–1) = 2)
- На второй странице (нулевой индекс первого элемента = 1 * 3 = 3) и (нулевой индекс последнего элемента = (1 * 3) + (3–1) = 5)
- На третьей странице (нулевой индекс первого элемента = 2 * 3 = 6) и (нулевой индекс последнего элемента = (2 * 3) + (3–1) = 8)
- На четвертой странице (первый элемент с нулевым индексом = 3 * 3 = 9) и (последний элемент с нулевым индексом = (3 * 3) + (3–1) = 11, что больше максимального доступного элемента. index (9), следовательно, последний элемент Zero-Index = 9)

Давайте посмотрим код
Подтвердив все уравнения, давайте посмотрим, как применить их в коде. Я предоставлю две реализации: одну на JavaScript, а другую на .NET C#.
Код JavaScript
Применение уравнений в виде функции расширения к JavaScript массиву.
Array.prototype.page = function(pageSize){
const self = this;
let actualPageSize = pageSize;
if(actualPageSize <= 0) {
actualPageSize = self.length;
}
let maxNumberOfPages = Math.max(1, Math.ceil(parseFloat(parseFloat(self.length) / parseFloat(actualPageSize))));
let pagesBoundries = {};
for(let pageZeroIndex = 0; pageZeroIndex < maxNumberOfPages; pageZeroIndex++) {
pagesBoundries[pageZeroIndex] = {
firstItemZeroIndex: (pageZeroIndex * actualPageSize),
lastItemZeroIndex: Math.min((pageZeroIndex * actualPageSize) + (actualPageSize - 1), self.length - 1)
};
}
return {
actualPageSize: actualPageSize,
numberOfPages: maxNumberOfPages,
pagesBoundries: pagesBoundries,
find: function(itemZeroIndex) {
return {
pageZeroIndex: parseInt(parseInt(itemZeroIndex) / parseInt(actualPageSize)),
itemZeroIndexInsidePage: parseInt(parseInt(itemZeroIndex) % parseInt(actualPageSize))
};
}
};
};
Теперь выполняем этот код:
let items = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
let pagingResult = items.page(3);
console.log(pagingResult);
Вернется:

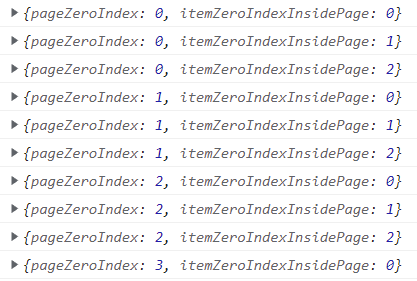
И, выполняя этот код:
console.log(pagingResult.find(0)); // { pageZeroIndex: 0, itemZeroIndexInsidePage: 0 }
console.log(pagingResult.find(1)); // { pageZeroIndex: 0, itemZeroIndexInsidePage: 1 }
console.log(pagingResult.find(2)); // { pageZeroIndex: 0, itemZeroIndexInsidePage: 2 }
console.log(pagingResult.find(3)); // { pageZeroIndex: 1, itemZeroIndexInsidePage: 0 }
console.log(pagingResult.find(4)); // { pageZeroIndex: 1, itemZeroIndexInsidePage: 1 }
console.log(pagingResult.find(5)); // { pageZeroIndex: 1, itemZeroIndexInsidePage: 2 }
console.log(pagingResult.find(6)); // { pageZeroIndex: 2, itemZeroIndexInsidePage: 0 }
console.log(pagingResult.find(7)); // { pageZeroIndex: 2, itemZeroIndexInsidePage: 1 }
console.log(pagingResult.find(8)); // { pageZeroIndex: 2, itemZeroIndexInsidePage: 2 }
console.log(pagingResult.find(9)); // { pageZeroIndex: 3, itemZeroIndexInsidePage: 0 }
Вернется:
Код .NET C#
Применение уравнений в форме метода расширения к .NET C# List.
public delegate ItemPosition FindItemPositionHandler(int itemZeroIndex);
public class PagingDescriptor
{
public int ActualPageSize { get; private set; }
public int NumberOfPages { get; private set; }
public PageBoundry[] PagesBoundries { get; private set; }
public FindItemPositionHandler Find { get; private set; }
public PagingDescriptor(
int actualPageSize,
int numberOfPages,
PageBoundry[] pagesBoundries,
FindItemPositionHandler find)
{
ActualPageSize = actualPageSize;
NumberOfPages = numberOfPages;
PagesBoundries = pagesBoundries;
Find = find;
}
}
public class PageBoundry
{
public int FirstItemZeroIndex { get; private set; }
public int LastItemZeroIndex { get; private set; }
public PageBoundry(int firstItemZeroIndex, int lastItemZeroIndex)
{
FirstItemZeroIndex = firstItemZeroIndex;
LastItemZeroIndex = lastItemZeroIndex;
}
}
public class ItemPosition
{
public int PageZeroIndex { get; private set; }
public int ItemZeroIndexInsidePage { get; private set; }
public ItemPosition(int pageZeroIndex, int itemZeroIndexInsidePage)
{
PageZeroIndex = pageZeroIndex;
ItemZeroIndexInsidePage = itemZeroIndexInsidePage;
}
}
public static class ListExtensionMethods
{
public static PagingDescriptor Page(this IList list, int pageSize)
{
var actualPageSize = pageSize;
if (actualPageSize <= 0)
{
actualPageSize = list.Count;
}
var maxNumberOfPages = (int)Math.Round(Math.Max(1, Math.Ceiling(((float)list.Count) / ((float)actualPageSize))));
return new PagingDescriptor(
actualPageSize,
maxNumberOfPages,
Enumerable
.Range(0, maxNumberOfPages)
.Select(pageZeroIndex => new PageBoundry(
pageZeroIndex * actualPageSize,
Math.Min((pageZeroIndex * actualPageSize) + (actualPageSize - 1), list.Count - 1)
)).ToArray(),
(itemZeroIndex) => new ItemPosition(
itemZeroIndex / actualPageSize,
itemZeroIndex % actualPageSize
)
);
}
}
Теперь выполняем этот код:
var items = new List<int> { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
var pagingDescriptor = items.Page(3);
Вернется:
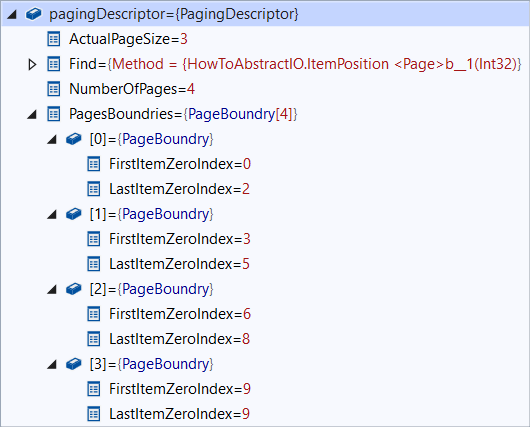
И, выполняя этот код:
var itemPosition01 = pagingDescriptor.Find(0); // { PageZeroIndex = 0, ItemZeroIndexInsidePage = 0 }
var itemPosition02 = pagingDescriptor.Find(1); // { PageZeroIndex = 0, ItemZeroIndexInsidePage = 1 }
var itemPosition03 = pagingDescriptor.Find(2); // { PageZeroIndex = 0, ItemZeroIndexInsidePage = 2 }
var itemPosition04 = pagingDescriptor.Find(3); // { PageZeroIndex = 1, ItemZeroIndexInsidePage = 0 }
var itemPosition05 = pagingDescriptor.Find(4); // { PageZeroIndex = 1, ItemZeroIndexInsidePage = 1 }
var itemPosition06 = pagingDescriptor.Find(5); // { PageZeroIndex = 1, ItemZeroIndexInsidePage = 2 }
var itemPosition07 = pagingDescriptor.Find(6); // { PageZeroIndex = 2, ItemZeroIndexInsidePage = 0 }
var itemPosition08 = pagingDescriptor.Find(7); // { PageZeroIndex = 2, ItemZeroIndexInsidePage = 1 }
var itemPosition09 = pagingDescriptor.Find(8); // { PageZeroIndex = 2, ItemZeroIndexInsidePage = 2 }
var itemPosition10 = pagingDescriptor.Find(9); // { PageZeroIndex = 3, ItemZeroIndexInsidePage = 0 }
Console.WriteLine($"PageZeroIndex: {itemPosition01.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition01.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition02.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition02.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition03.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition03.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition04.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition04.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition05.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition05.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition06.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition06.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition07.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition07.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition08.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition08.ItemZeroIndexInsidePage}");
Console.WriteLine($"PageZeroIndex: {itemPosition09.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition09.ItemZeroIndexInsidePage}");
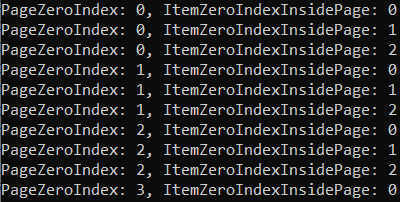
Console.WriteLine($"PageZeroIndex: {itemPosition10.PageZeroIndex}, ItemZeroIndexInsidePage: {itemPosition10.ItemZeroIndexInsidePage}");
Вернется:

Заключительные слова
Вот и все. Это наиболее важные уравнения, которые вам необходимо знать, чтобы применять пейджинг в любой ситуации.
Вы также можете использовать примеры кода, чтобы применить их к своему собственному проекту, используя любой язык или платформу, которую вы используете.
Вот и все, надеюсь, вам было так же интересно читать эту статью, как мне было ее писать.
Также опубликовано здесь
Оригинал

