Деликатная математика за быстрым сжатием и прибылью в LLMS
15 июля 2025 г.Таблица ссылок
Аннотация и 1. Введение
Основные помещения для наших моделей
2.1. Как взимаются LLM
2.2 Анедотальная модель из промышленности
2.3 Выбор затрат в модели
2.4 Почему несколько сценариев
Теоретическая модель решения
3.1 Как смоделировать успех
Модель для коммерческих операций на основе одной транзакции
4.1 Пример использования модели
4.2 Анализ модели
4.3 Обсуждение рентабельности рентабельности по сравнению
Моделирование проблемы бинарной классификации
5.1 Локальный анализ чувствительности
5.2 Глобальный анализ чувствительности методом SOBOL
Связанная работа
Будущая работа
Заключение, ссылки и подтверждения
4.2 Анализ модели
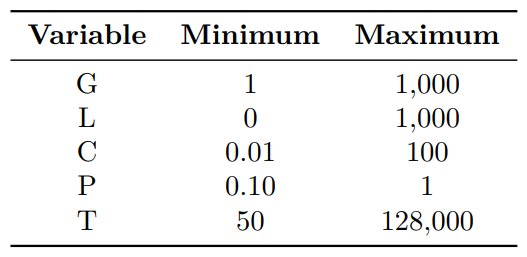
Мы должны отметить, что из -за использования LLM в коммерческом контексте неопределенности будут в основном в G, L и P. Было бы разумно ожидать нормальное распределение вероятностей для P и нормальное или даже распределение вероятностей власти для G и L., поскольку G и L являются бизнес -ценностями, а P - результаты бизнеса, которые поступают в соответствие с TASKS AI, эти значения не находятся под прямым контролем проектной команды. Мы помним, что полная модель вероятности успеха должна начинаться с уравнения 17, но это выходит за рамки этой статьи.
С другой стороны, t, то есть размер транзакции в токенах, он больше находится под контролем команды проекта, поскольку она зависит от размера используемых данных и желаемых, при вводе и выходе, а также от размера подсказки. Следует также ожидать нормального или распределения вероятности мощности для T., наконец, для одного выбранного LLM C фактически является постоянной, и нам нужно только понять его влияние на решение, когда рассматривается более одного LLM.
Looking at Equation 18, we can also see that if G and L are large and T small, the factor CT will be small and E[E] will be mainly a function of GP −L(1−P), and since G and P are expected to have the same distribution for a single business task, P would have the greater impact. Это может значительно повлиять на оценку методов быстрого сжатия, таких как Llmlinguajiang et al. [2023a, b], Pan et al. [2024] для небольших подсказок. Например, предположим, что задача классификации с использованием транзакции токена 1000 может привести к прибыли от 10 долларов США или убытке в 1 доллар США. Его стоимость составит 0,005 долл. США в GPT 4O. Таким образом, сжатие подсказки 20 × сэкономит 0,00475 долл. США в КТ. Между тем, каждый 1%, потерянный в P, приведет к потере GP - L (1 - P) в размере 0,11 долл. США. С другой стороны, для маленьких G и L и более крупного T, сжатие может быть эффективным.
Принимая во внимание все это, мы решили выполнить как локальный, так и глобальный анализ чувствительности, чтобы понять влияние параметров на E [E] и E [R]. Мы понимаем, что локальная чувствительность легче понять и разумна в этом случае, в то время как глобальная чувствительность теоретически сильнее; Поэтому мы также анализируем линейность функций, чтобы понять, насколько действителен локальный анализ.
4.2.1 Локальный анализ чувствительности
Этот первый анализ чувствительности является локальным и качественным. Это осуществляется путем оценки частичных производных E [E] по отношению к каждой переменной в их соответствующих интервалах. Это дает представление о том, насколько чувствителен E [E] к изменениям в каждом параметре в диапазоне вариации.
Taking into account Equation 18, it is possible to find all the partial derivatives for variables G, C, T, P and L.
Частичными производными для E [E] являются:
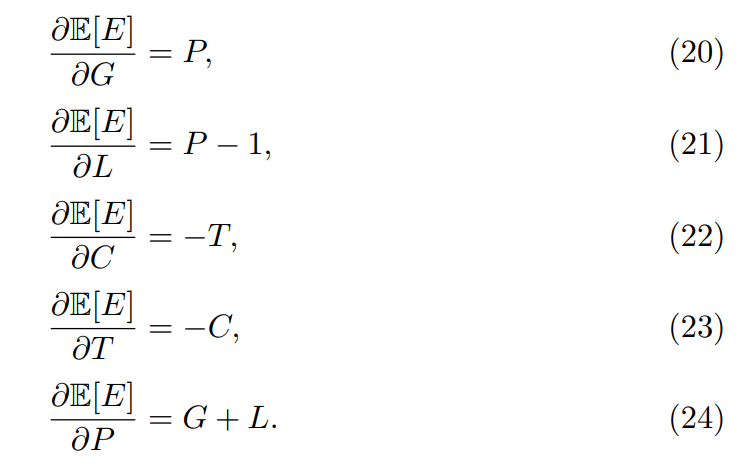
Гессиан E [E] в основном состоит из нулей, что указывает на довольно линейное поведение, которое было бы очень приемлемо для локального анализа.
Точно так же частичные производные для e [r] являются:
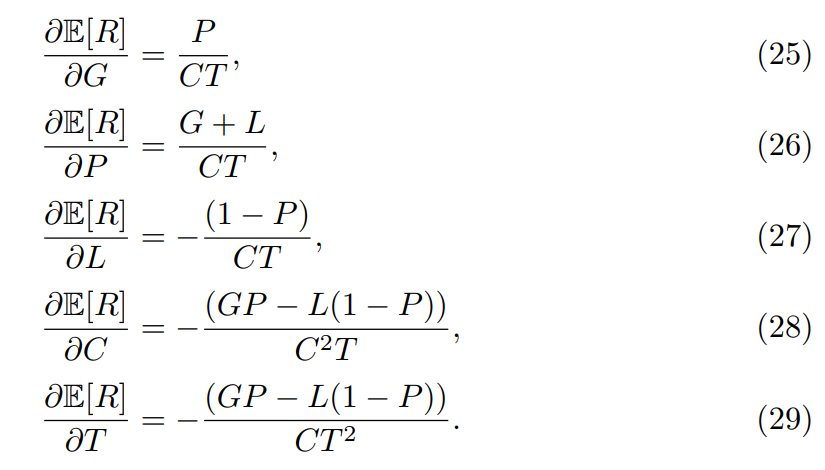
Таким образом, гессская матрица h e [r] относительно переменных g, c, t, l и p - это:
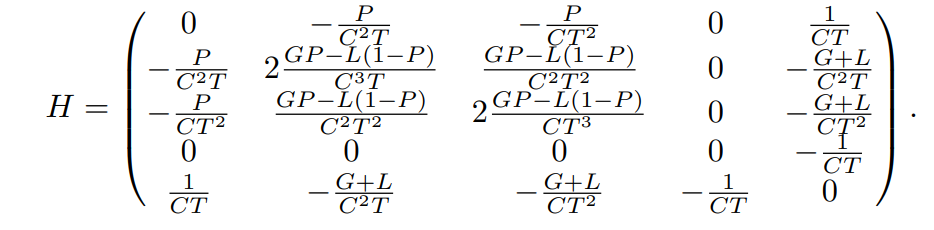
Гессианская матрица E [R] имеет меньше нулей, и небольшое значение C, обнаруженное в знаменателе большинства частичных производных, принесет большие значения. Это отражение является проблемой для локального анализа чувствительности; Тем не менее, просмотр частичных производных по -прежнему позволяет получить некоторые преимущества в отношении интерпретации.

4.2.2 Глобальный анализ чувствительности доходов с помощью техники SOBOL
Хотя локальный анализ чувствительности рассматривает одну переменную каждый раз в окрестностях точки, и, следовательно, является лишь адекватным, если так, для линейных и в основном линейных функций, глобальный анализ может изучать эффект всех переменных одновременно, для конкретных распределений, даже в случае нелинейности [Saltelli et al., 2004, 2008].
Sobol [2001] предложил метод для анализа глобального чувствительности, основанный на запуске модели с отбором выборки, генерируемой в определенных помещениях, и создал разложение дисперсии, которое позволяет расчет набора индексов чувствительности.
Индекс Sobol первого порядка измеряет индивидуальный вклад каждой входной переменной в дисперсию в выходе модели, игнорируя взаимодействия с другими переменными. В более простых терминах он количественно определяет, сколько неопределенности в выходе модели может быть напрямую связана с изменениями в конкретном входе, в то время как все остальные входы удерживаются фиксированными. This quantification is performed between values 0 and 1 [Sobol, 2001].
Индекс общего порядка SOBOL определяет общий вклад входной переменной в выходную дисперсию, учитывая как его индивидуальный эффект, так и его взаимодействие с другими переменными. По сути, он измеряет влияние переменной на результаты путем учета всех возможных способов, которыми она может влиять на результат, включая его комбинированные эффекты с другими переменными. Этот индекс также колеблется между значениями 0 и 1, указывая на долю выходной изменчивости, приписываемой общему влиянию заданной входной переменной [Sobol, 2001].
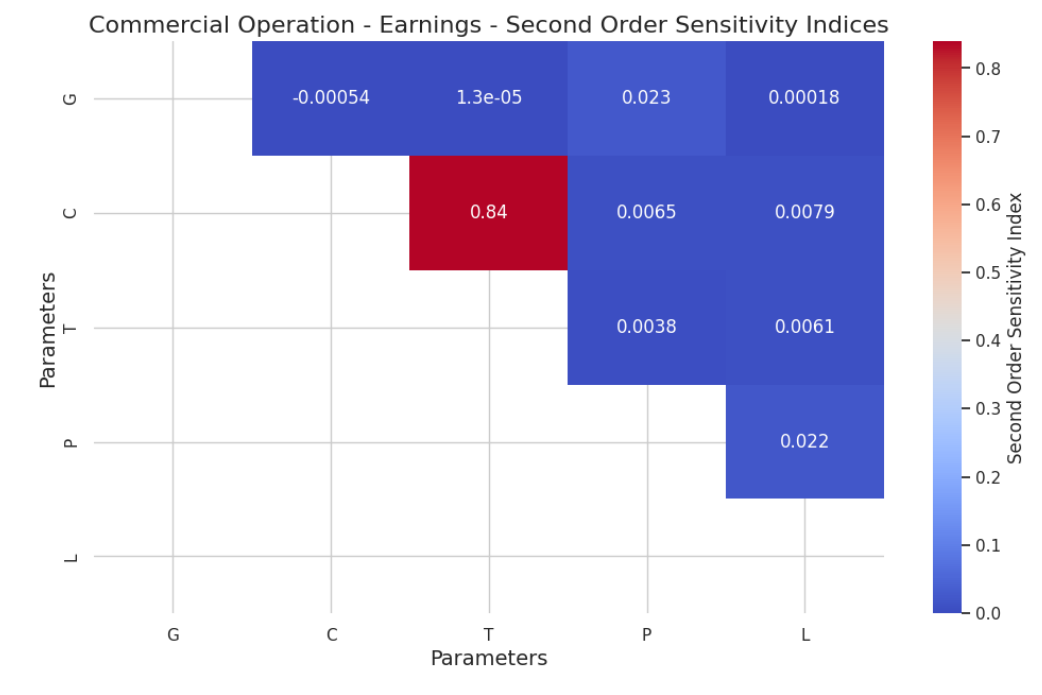
Наконец, второй заказ и более высокие порядки индекс SOBOL является расширением индекса первого порядка и используется для измерения комбинированного эффекта или взаимодействия между парами или кортежями входных переменных при дисперсии выхода модели. В то время как индекс первого порядка фокусируется на индивидуальном вкладе каждой переменной, индекс второго порядка рассматривает, как взаимодействие между двумя переменными способствует неопределенности в выводе, помимо того, что можно было бы ожидать на основе отдельных эффектов каждой переменной [Sobol, 2001]. Это обеспечивает хорошее визуальное представление комбинированного эффекта пары переменных в матрице.

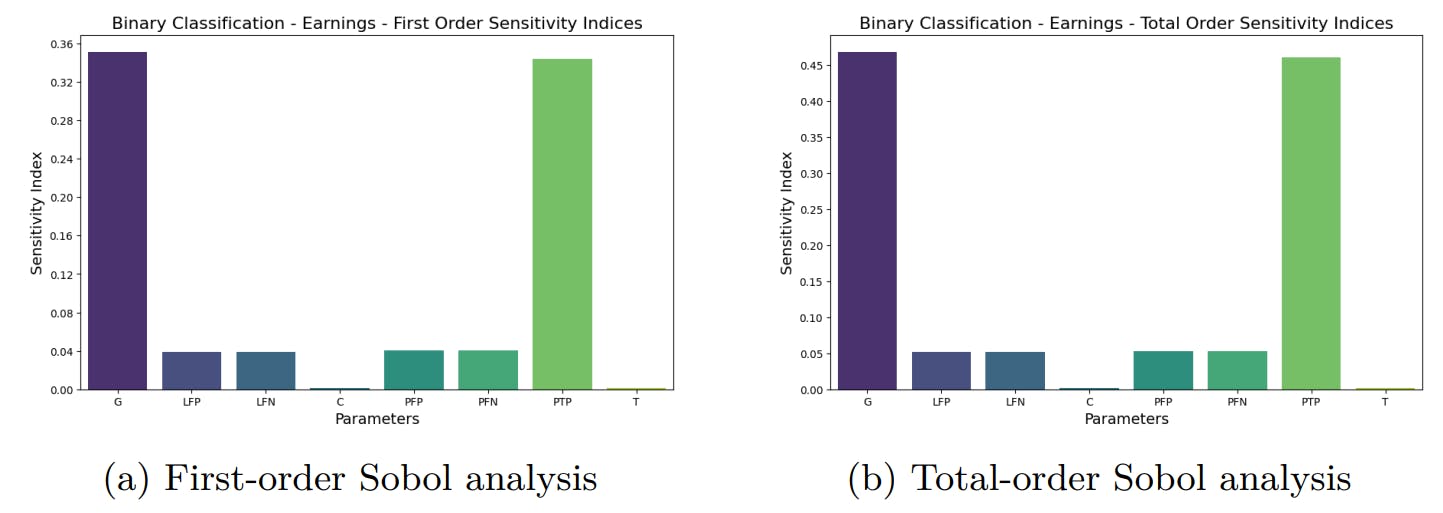
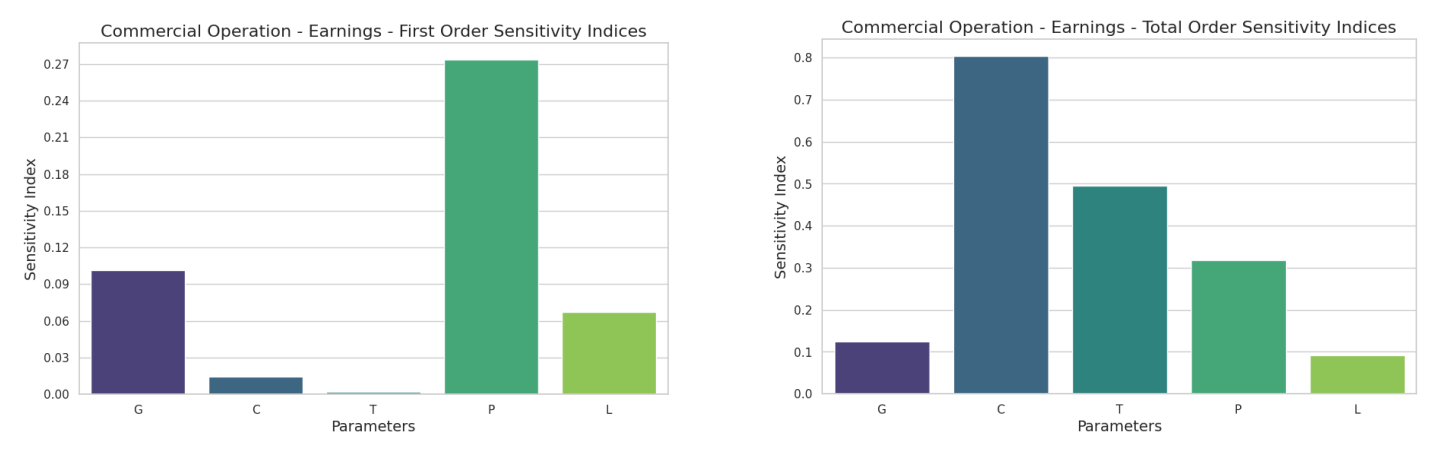
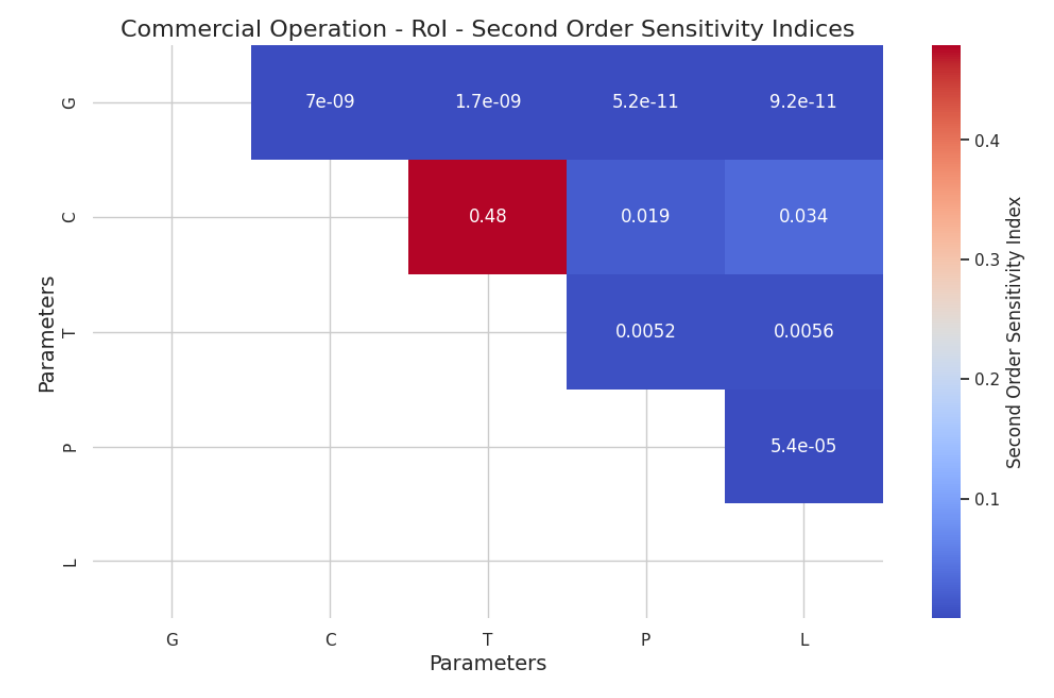
Из глобального анализа чувствительности доходов для модели коммерческой операции можно увидеть, что значение P, очевидно, является наиболее важным фактором в анализе первого порядка Рисунок 2A. Для общего индекса порядка рисунок 2B показывает важность C и T, что также отражается во значениях второго порядка, показанные на рисунке 3, который показывает четкое преобладание пары C и T в качестве пары. Продукт КТ является общей стоимостью транзакции.
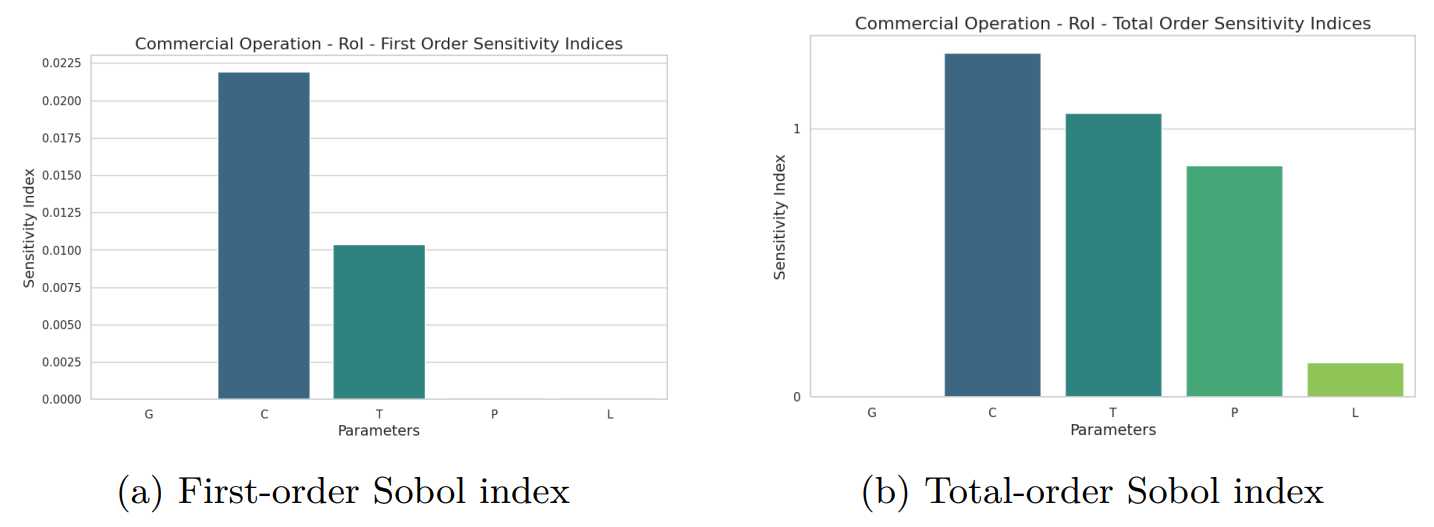
Анализ чувствительности ROI для модели коммерческой операции показывает, что ROI особенно чувствителен к изменениям C, T и P для общего порядка в пределах заданных диапазонов. В частности, комбинация C и T оказывает большее влияние на изменение ROI второго порядка. Поскольку C и T уже были наиболее важными факторами в анализе доходов, ожидается, что они увидят их значение в ROI, где они играют большую роль в конечной стоимости уравнения ROI.
Доходы в основном чувствительны к C и T, причем P играет важную роль. Основываясь на этом сценарии, следует обратить внимание на хороший прогноз T и P, поскольку C будет зафиксирован для определенного LLM.
4.3 Обсуждение рентабельности рентабельности по сравнению
Выбор между проектами, которые различаются по их потенциальной прибыли и рентабельности инвестиций, является распространенной дилеммой, с которой сталкиваются менеджеры проектов [Институт управления проектами, 2021]. Выбор между проектом с меньшим доходом, но более высоким ROI, и другим с большим доходом, но более низким ROI включает в себя стратегический процесс принятия решений, который рассматривает различные финансовые и нефинансовые факторы.
Хотя ROI является важнейшей метрикой, абсолютный потенциал заработка проекта не следует упускать из виду. Проект с более низкой ROI, но более высокий общий доход может быть более полезным, если дополнительный доход значительно влияет на перспективы финансового здоровья или роста компании. Тем не менее, в рамках бюджетных ограничений проекты с более низкими затратами и более высокой рентабельности инвестиций могут быть более осуществимыми, даже если их общий заработок ниже. На самом деле, поскольку обычно это легко обмениваться LLM, это может быть начальной загрузкой. Анализ текущего и будущего денежного потока может помочь с решением.
Авторы:
(1) Джеральдо Xexéo, Programa de Engenharia de Sistemas E Computação - Coppe, Universidade Federal Do Rio De Janeiro, Бразиль;
(2) Филипе Брайда, Destamento de Ciência da Computação, Universidade Federal Rural Do Rio de Janeiro;
(3) Маркус Паррейс, Programa de Engenharia de Sistemas e Computação - Coppe, Universidade Federal Do Rio de Janeiro, Бразил и Координадория де Энгенхария де Продушен - Coenp, Cefet/RJ, Unidade Nova Iguaçu;
(4) Пауло Ксавье, Programa de Engenharia de Sistemas E Computação - Coppe, Universidade Federal Do Rio de Janeiro, Бразил.
Эта статья есть
Оригинал
