
Снижение сборов блокчейна с помощью R2-TFRM и случайной случайности в цепочке
30 июня 2025 г.Таблица ссылок
Аннотация и 1. Введение
Связанная работа
Предварительные
3.1 TFMS: желательные свойства
3.2 Механизм перераспределения Groves (RM)
Идеал-TFRM: невозможность достижения строго положительного индекса перераспределения
Механизм перераспределения платы за транзакцию (TFRM)
R-TFRM: TFRM, надежный для манипуляций с шахтером
6.1 R-TFRM: анализ влияния манипуляций с шахтером на скидку и доходы от шахтеров
R2-TFRM: надежный и рациональный TFRM
Заключение и ссылки
A. Доказательства для результатов раздела 4 и 5
B. Доказательства для результатов раздела 6
C. Доказательства для результатов раздела 7
R2-TFRM: надежный и рациональный TFRM

R2 -TFRM: случайная случайность в цепочке.Как указано, каждая транзакция получает скидку с вероятностью 𝛼. Подобно другим TFM [8], мы используем доверенную случайность в сети для этой рандомизации. Исследователи предложили такие надежные рандомизированные протоколы с использованием различных криптографических примитивов [3, 10]. Примечательно, что шахтер блока не может оказать какое -либо влияние на эту рандомизацию.

Доказательство эскиза. Мы разделяем доказательство на две части.


R2 -TFRM: анализ манипуляции с шахтером.Как и R -TFRM, R2 - TFRM также обеспечивает строго положительный RRI даже с манипуляциями на шахтере, как формально указано в теореме 7.
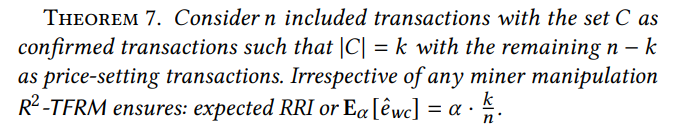
Доказательство эскиза. Результат следует из аналогичного результата в теореме 5 для R -TFRM и того факта, что майнер не имеет контроля над рандомизацией в R2 -TFRM.

Обсуждение по TFRM.Учитывая, что текущая литература TFM предполагает, что пользователи и шахтеры являются миопическими, мы считаем, что перераспределение избытка является более эффективным в сокращении чистых платежей, выплачиваемых пользователями. Другое желательное свойство в TFMS - это предсказуемые сборы за транзакцию, то есть снижение волатильности сборов, уплаченных пользователями. Например, EIP-1559 [5] использует детерминированную функцию, основанную на предыдущем потреблении блока для расчета минимальной пороговой платы, определяемой сетью (вызываетсябазаплата) оплачивается каждым пользователем. Пользователи также могут заплатитьприоритетПлата за базовую плату за стимулирование шахтеров включить их транзакции. Базовая комиссия направлена на снижение волатильности платы и направлена на то, чтобы получить рыночную цену очистки. Важно отметить, что эта минимальная пороговая платасгорел- Передается на невыразимый адрес - подразумевает, что шахтер не получает эту плату в качестве дохода. Мы видим, что сжигание некоторой части платы необходимо, чтобы гарантировать такие свойства. В таких механизмах приоритетная плата, рассчитанная после сжигания, может быть дополнительно уменьшена с использованием TFRM.
8 Заключение
В этой статье мы утверждали важность минимизации пользовательских затрат в TFM. Наша ключевая идея состоит в том, чтобы использовать основанный на механизме перераспределения подход для определения сборов за транзакцию, который мы называем механизмом перераспределения платы за транзакцию (TFRM). Из -за стратегических манипуляций с шахтером мы сначала показываем, что гарантирование строго положительной скидки в TFRM и других желательных свойствах невозможно. Следовательно, мы предлагаем R-TFRM, который обеспечивает строго положительные скидки даже в худшем случае, но на компромисс на ИК шахтеров. Тем не менее, мы показываем, что в R-TFRM стратегический шахтер никогда не будет нести негативную утилиту, в то же время гарантируя строго положительные скидки для пользователей. Мы также предлагаем R2 -TFRM, который использует необоснованность блокчейна, чтобы гарантировать строго положительную скидку для пользователей, а также уважать ИК шахтера.
Будущая работа.Будущие направления могут исследовать TFRM с рандомизированными функциями скидок, которые, вероятно, могут удовлетворить более сильные представления о IC и IR. Другой подход может заключаться в изучении нелинейных функций скидок, которые в среднем могут обеспечить лучший индекс перераспределения. Кроме того, в отличие от этой работы, будущая работа также может изучать транзакции с различными размерами.
Ссылки
[1] Мартин Дж. Бейли. 1997. Процесс выявления спроса: распределить избыток. Общественный выбор 91, 2 (1997), 107–26. https://econpapers.repec.org/repec:kap: pubcho✌91: y: 1997: i: 2: p: 107-26
[2] Суйя Басу, Дэвид Исли, Морин О'Хара и Эмин Сирер. 2019. StableFees: предсказуемый рынок платежей для Cryptocurrencie. Доступно по адресу SSRN 3318327 (2019).
[3] Адития Бхат, Нибеш Шрестха, Чжунганг Луо, Аникет Кейт и Картик Наяк. 2021. Рэндпипер-реконфигурация, благоприятные случайными маяками с квадратичной связи. В ACM CCS. 3502–3524.
[4] Vitalik Baterin et al. 2014. Смарт-контракт следующего поколения и децентрализованная платформа приложений. Белая бумага 3, 37 (2014), 2–1.
[5] Виталик Бутерин, Эрик Коннер, Рик Дадли, Мэтью Слиппер, Ян Норден и Абдельхамид Бахта. 2019. EIP-1559: изменение рынка плат для цепочки ETH 1.0. eips.ethereum.org/eips/eip-1559.
[6] Руджеро Кавалло. 2006. Оптимальное принятие решений с минимальными отходами: стратегическое перераспределение выплат VCG. В Proc. 5 -го инт. Совместный конф. об автономных агентах и многогентных системах (AAMAS'06). Хакодат, Япония, 882–889. http://econcs.seas.harvard.edu/files/econcs/files/cavallo-redis.pdf
[7] Руджеро Кавалло. 2008. Эффективность и перераспределение в конструкции динамического механизма. В Proc. 9 -й ACM Conf. по электронной торговле (EC’08). Чикаго, Иллинойс, 220–229. http://econcs.seas.harvard.edu/files/econcs/files/cavallo-ec08.pdf
[8] Хао Чунг и Элейн Ши. 2023. Основы проектирования механизма плата за транзакцию. В ACM-SIAM Soda. 3856–3899.
[9] Эдвард Кларк. 1971. Многоарные цены на общественные блага. Общественный выбор 11, 1 (1971), 17–33.
[10] Сурав Дас, Винит Кришнан, Ирен Мириам Исаак и Линг Рен. 2022. SPRT: масштабируемый распределенный маяк случайности с прозрачной установкой. В IEEE S & P.
[11] Джеффрой де Клиппель, Виктор Народицкий, Мария Полукаров, Эми Гринвальд и Николас Р. Дженнингс. 2014. Уничтожьте, чтобы спасти. Игры и экономическое поведение 86, C (2014), 392–404.
[12] Пол Дюттинг, Чжэ Фэн, Харикришна Нарасимхан, Дэвид Паркс и Саи Шриватса Равиндранат. 2019. Оптимальные аукционы через глубокое обучение. В ICML. PMLR, 1706–1715.
[13] Бой Фалтингс. 2005. Бюджетная сбалансированная, совместимая с стимулом для социального выбора. В агентском опосредованном электронной коммерции VI. Теории и разработка распределенных механизмов и систем: семинар AAMAS 2004, AMEC 2004. 30–43.
[14] Матеус В. Х. Феррейра, Даниэль Дж. Мороз, Дэвид С. Паркс и Митчелл Стерн. 2021. Динамические механизмы рассылки на рынок транзакции блокчейна. В конференции ACM по авансам в области финансовых технологий (кормовой). 86–99.
[15] Теодор Гроувс. 1973. Стимулы в командах. Econometrica 41, 4 (1973), 617–31.
[16] Суджит Гуджар и Ю. Нарахари. 2011. Механизмы перераспределения для назначения гетерогенных объектов. J. Artif. Инт. Резерв 41, 2 (май 2011), 24. [17] Mingyu Guo. 2012. В худшем случае оптимальное перераспределение выплат VCG на аукционах гетерогенных элементов с спросом на единицу. В аамах. 745–752.
[18] Минью Го и Винсент Коницер. 2007. В худшем случае оптимальное перераспределение выплат VCG. В ACM EC. 30–39.
[19] Минью Го и Винсент Коницер. 2008. Лучшее перераспределение с неэффективным распределением на аукционах с несколькими единицами с спросом на единицу. В ACM EC. 210–219.
[20] Минью Го и Винсент Коницер. 2009. В худшем случае оптимальное перераспределение выплат VCG на аукционах с несколькими единицами. Игры и экономическое поведение 67, 1 (2009), 69–98.
[21] Джейсон Д. Хартлин и Тим Гроугарден. 2008. Оптимальный проект механизма и сжигание денег. В материалах сорокового ежегодного симпозиума ACM по теории вычислений (Виктория, Британская Колумбия, Канада) (Stoc ’08). ACM, Нью -Йорк, Нью -Йорк, США, 75–84. https://doi.org/10.1145/1374376.1374390
[22] Махимна Келкар, фанат Чжан, Стивен Голдфедера и Ари Джуэльс. 2020. Орден на византийский консенсус. В ежегодной международной криптологической конференции (крипто). 451–480.
[23] Клаус Курсаве. 2020. Венди, Виджет «Хорошая маленькая справедливость: достижение справедливости порядка для блокчейнов». В конференции ACM по авансам в области финансовых технологий (кормовой). 25–36.
[24] Падала Маниша, CV Jawahar и Sujit Gujar. 2018 год. В материалах 17 -й Международной конференции по автономным агентам и многоагентным системам. 345–353.
[25] Эрик Маскин, Дж. Дж. Лаффон и Дж. Дж. Лаффонт. 1979. Дифференциальный подход к ожидаемой полезности максимизации механизмов. Северная Голландия, 289-308.
[26] Джоннатан Мессиас, Мохамед Альзаят, Балакришнан Чандрасекаран и Кришна П Гуммади. 2020. На блокчейне время совершения: анализ того, как шахтеры выбирают биткойн -транзакции. Во втором международном семинаре по интеллектуальным данным для блокчейна и распределенной книги (SDBD2020).
[27] Херве Мулен. 2009. Практически сбалансированные механизмы VCG для назначения нескольких объектов. Журнал экономической теории 144, 1 (2009), 96–119.
[28] Роджер Б. Майерсон и Марк Саттертвайт. 1983. Эффективные механизмы для двусторонней торговли. Журнал экономической теории 29, 2 (1983), 265–281.
[29] Сатоши Накамото. 2008. Биткойн: одноранговая электронная система денежных средств. Децентрализованный бизнес -обзор (2008), 21260.
[30] Ариэль Орда и Ори Роттенштрех. 2021. Обеспечение справедливости в упорядочении транзакций блокчейна. Одноранговые сети и приложения 14, 6 (2021), 3660–3673.
[31] Дэвид С. Паркс, Джаянт Р. Калагнанам и Марта Эзо. 2001. Достижение бюджетного баланса с схемами платежей на базе Викри на биржах. В Proc. 17 -я Международная совместная конференция по искусственному интеллекту (IJCAI’01). 1161–1168. http://econcs.seas.harvard.edu/files/econcs/files/combexch01.pdf
[32] Райан Портер и Йоав Шохам. 2003. О мошенничестве на запечатанных аукционах. В материалах 4 -й конференции ACM по электронной торговле. 76–84.
[33] Тим Гроуггарден. 2021. Конструкция механизма плата за транзакцию. В конференции ACM по экономике и вычислениям (ACM EC). 792.
[34] Shoeb Siddiqui, Ganesh Vanahalli и Sujit Gujar. 2020. BitCoinf: достижение справедливости для биткойнов в модели только в плате за транзакцию. В аамах. 2008–2010.
[35] Корвин Смит. 2023. Награды и штрафы. ethereum.org/en/developers/docs/consensus-mechanisms/pos/rewards-andpenalties/. [Онлайн].
[36] Андреа Точетти, DJ Strouse, Marta Garnelo, Thore Graepel и Yoram Bachrach. 2019. Нейронная архитектура для проектирования правдивых и эффективных аукционов. Arxiv Preprint arxiv: 1907.05181 (2019).
[37] В. Викри. 1961. Контроль, аукционы и конкурентные герметичные тендеры. Журнал финансов 16, 1 (март 1961 г.), 8–37.
[38] Ycharts. 2022. Биткойн -транзакции в день. ycharts.com/indicators/bitcoin_ transactions_per_day.
[39] Ycharts. 2022. Транзакции Ethereum в день. ycharts.com/indicators/ ethereum_transactions_per_day.
[40] Зишуо Чжао, Си Чен и Юань Чжоу. 2022. Байесовский намек-интенсивный механизм для распределения платы за транзакцию блокчейна. В конференции по безопасности Crypto Economics (CESC).
Авторы:
(1) Sankarshan Damle, IIIT, Хайдарабад, Хайдербад, Индия (Sankarshan.damle@research.iiit.ac.in);
(2) Маниша Падала, IISC, Бангалор, Бангалор, Индия (manishap@iisc.ac.in);
(3) Суджит Гуджар, IIIT, Хайдарабад, Хайдербад, Индия (sujit.gujar@iiit.ac.in).
Эта статья есть
Оригинал
