Наивный байеса превосходит конкурентов в области аудита финансовых, текстовых и сетевых данных

Таблица ссылок

• Аннотация и 1. Введение
• 2. Обзор литературы
  • 3. Наивный байесовский классификатор
• 4. Результаты
  • 5. Дискуссия
  • 6. Выводы и ссылки

4. Результаты

Это исследование генерирует три эксперимента, чтобы проиллюстрировать преимущества и ограничения комбинирования алгоритма машинного обучения с выборкой. Первый эксперимент демонстрирует, что интеграция машинного обучения помогает избежать смещения отбора проб и сохранять случайность и изменчивость. Второй эксперимент показывает, что предлагаемые работы помогают образец неструктурированных данных. Окончательный эксперимент показывает, что гибридный подход уравновешивает репрезентативность и рискованность при выборочном аудиторском доказательстве.

Ссылаясь на предыдущее исследование [15], реализация интеграции машинного обучения с выборкой лучше на основе точных результатов классификации, предоставленных алгоритмом машинного обучения. Следовательно, это исследование выбирает случайный лесной классификатор и модель опорных векторных машин с ядром радиальной базисной функции в качестве базовых моделей.

4.1. Эксперимент 1

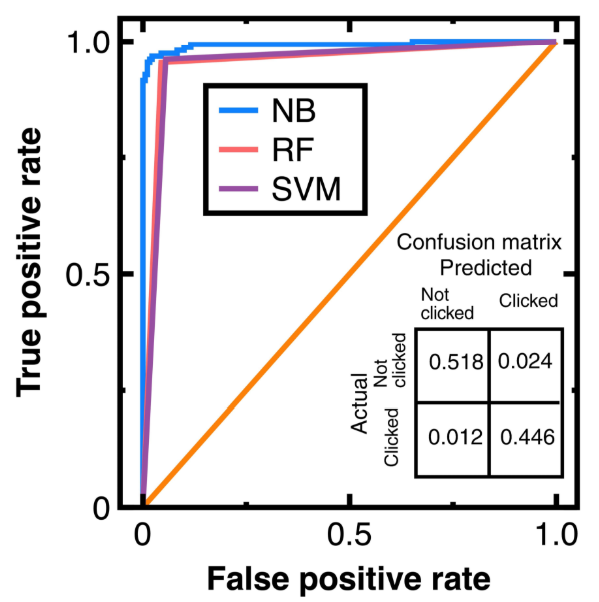
Чтобы избежать ошибок отбора проб [15] [15], необходимо изучение вывода точности классификации по уравнениям (3)-(4). На рисунке 4 показаны полученные кривые ROC, в которых NB, RF и SVM являются аббревиатурами наивных байесов, случайных лесов и опорных векторных машин. На этом рисунке также показан вывод матрицы путаницы по уравнениям (3)-(4). Его компоненты были нормализованы на основе количества тестовых данных. Более того, это исследование вычисляет:

Дальнейшее вычисление показателя F1 из уравнений (14)-(15)

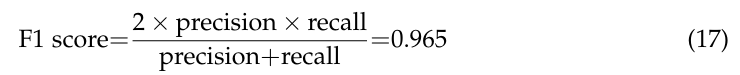
Между тем, расчет AUC на рисунке 4 получает 0,965 (уравнения (3)-(4)), 0,953 (классификатор случайного леса) и 0,955 (модель опорных векторных машин с ядром радиальной базисной функции). Эти значения AUC указывают, что уравнения (3)-(4) слегка превосходят модель случайного классификатора и векторов опорных лесов с ядром радиальной базисной функции во избежание ошибок в рамках отбора проб и под прикрытием. Тем не менее, все три алгоритма являются хорошими моделями.

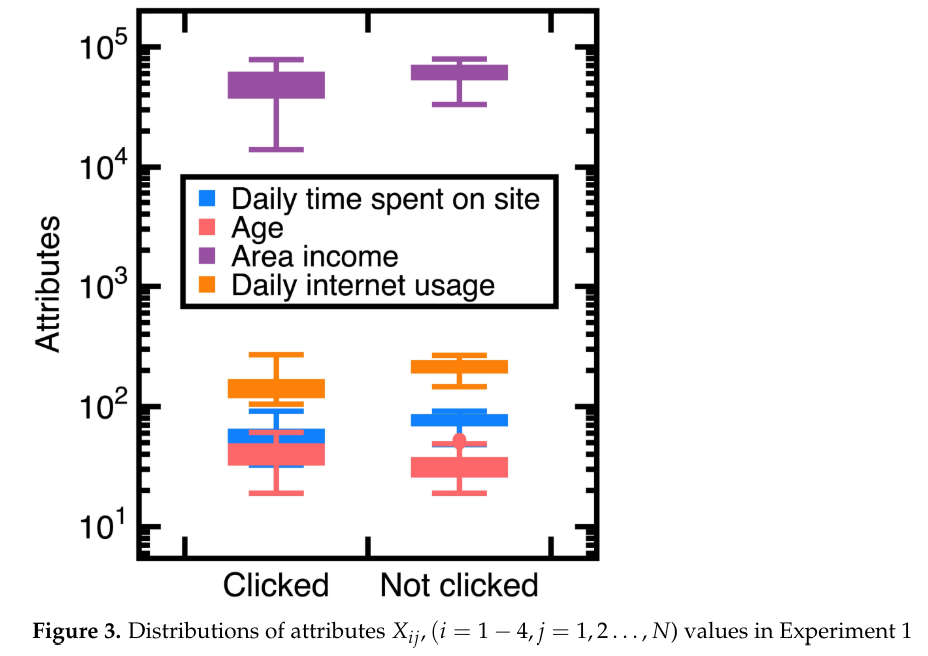
Наша цель для тестирования Раздел 3.1 - попробовать непредвзятое представление экспериментальных данных с интеграцией машинного обучения. На рисунке 5 показаны полученные аудиторские доказательства с 50 % доверительным интервалом для каждого класса. Гистограммы на верхних и правых сторонах этой фигуры сравнивают распределения оригинальных клиентов и аудиторские доказательства. На этом рисунке световые и тяжелые серо -точки обозначают экспериментальные данные, тогда как красные и синие цветы отмечают доказательства аудита. Общее количество синих и красных точек на рисунке 5 равно 250 соответственно. Замена полученных аудиторских доказательств в уравнение (7) получает индексы репрезентативности, перечисленные в «Легенде» на рисунке 5.

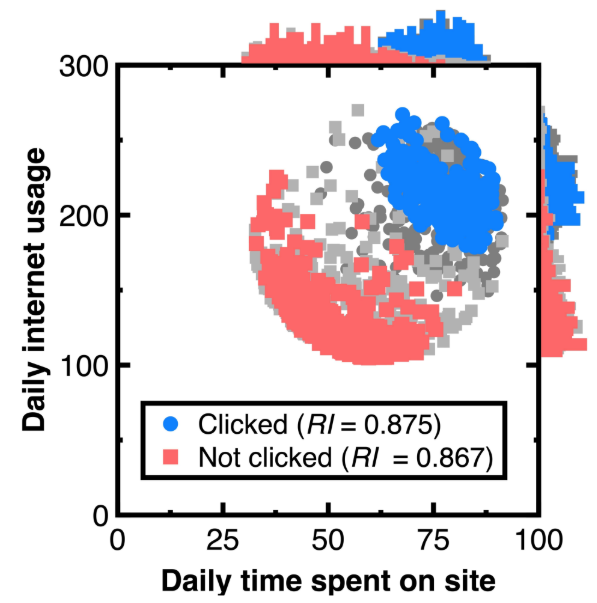
Расчет статистики теста Колмогорова-Смирнова гарантирует, что аудиторские доказательства на рисунке 5 являются беспристрастными и представителями первоначальных клиентов. Если полученная статистика теста Колмогоровсмирнова ниже критического значения для заключения этой статистики теста, первоначальные клиенты и аудиторские доказательства происходят из того же распределения вероятностей. Таким образом, мы можем снизить риск системных ошибок или смещений в оценке атрибутов клиентов.

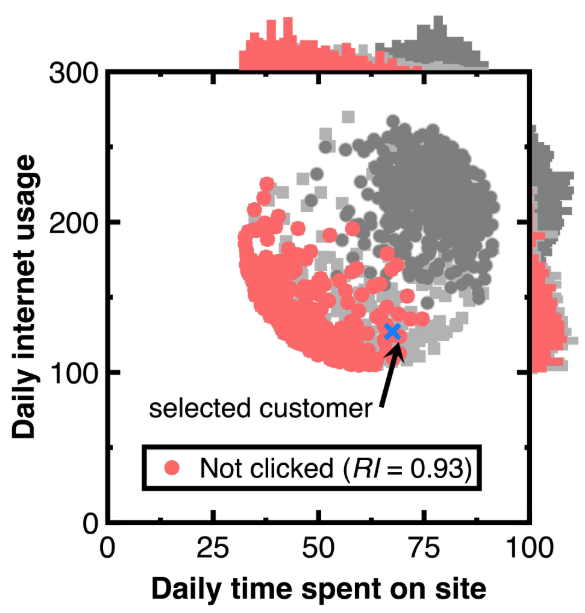
У нас есть еще одна цель сохранения изменчивости в разделе тестирования 3.2. Как отмечено синим крестом на рисунке 6, выберите клиента с прогнозируемой апостериорной вероятностью 0,999. В заголовке рисунка 6 перечислены атрибуты этого клиента. Другие клиенты, имеющие отношение к этому клиенту, привлекаются в качестве аудиторских доказательств и отмечаются с использованием красных точек на рисунке 6. Кроме того, мы все еще используем световые или тяжелые точки серого, представляющие экспериментальные данные и гистограммы, кроме рисунка 6, чтобы описать распределение аудиторских доказательств. Поскольку знаменатель PR (CI) уравнения (11) равен 0,5. Установка порога σ2 на 1,9999 рассматривается. Замена полученных аудиторских доказательств в уравнение (7) дает индекс репрезентативности RI в легенде на рисунке 7. Подсчет количества нарисованных аудиторских доказательств дает 294.

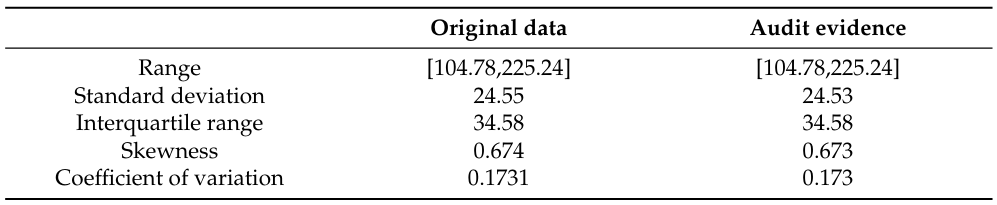
В таблице 1 сравнивается изменчивость между исходной «переменной ежедневного использования интернета» и аудиторными доказательствами. Мы используем диапазон, стандартное отклонение, межквартильный диапазон и коэффициент вариации для измерения изменчивости.

Измерение изменчивости помогает понять форму и распространение аудиторских доказательств. В таблице 1 показано, что аудиторские доказательства сохраняют изменчивость.

4.2. Эксперимент 2

Сообщение о спаме является одним из неструктурированных данных, которые не отображались в обычной выборке. В этом эксперименте это исследование вводит набор данных, содержащий 5572 сообщения, а 13 % из них - спам. Это исследование случайным образом выбирает 75 % из них в качестве данных поезда. Остальные 25 % являются данными тестирования. При реализации этого эксперимента первым шагом является предварительная обработка этих данных поезда и тестирования путем векторизации каждого сообщения в серию ключевых слов. Мы используем словарь, чтобы выбрать ключевые слова кандидата. Подсчет их частоты выполняется в следующий раз. Классификация сообщений HAM и SPAM выполняется путем установки переменной класса CI (1 ≤ I ≤ N), указывая на сообщение о спаме или ветчине, а атрибуты являются частотой ключевых слов.

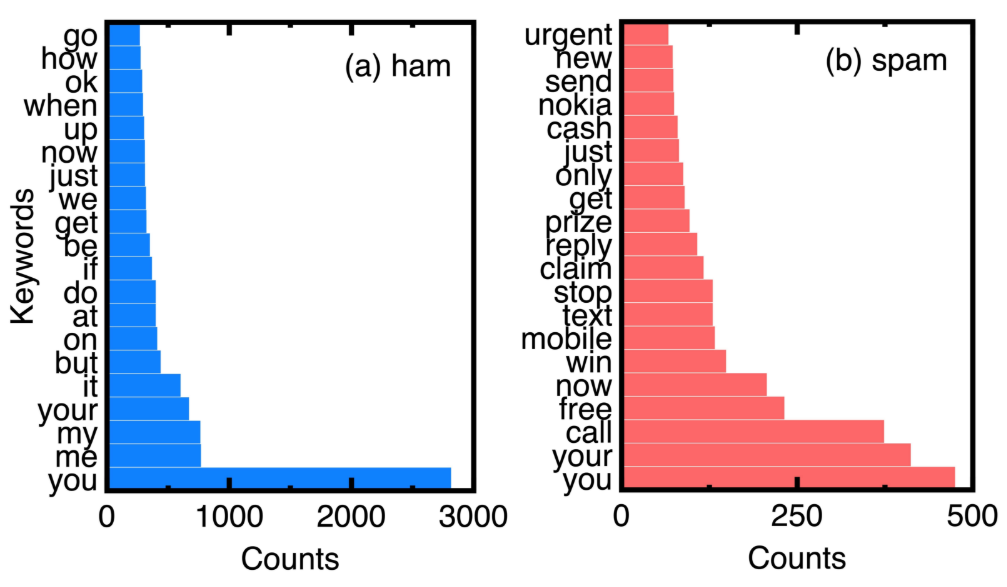
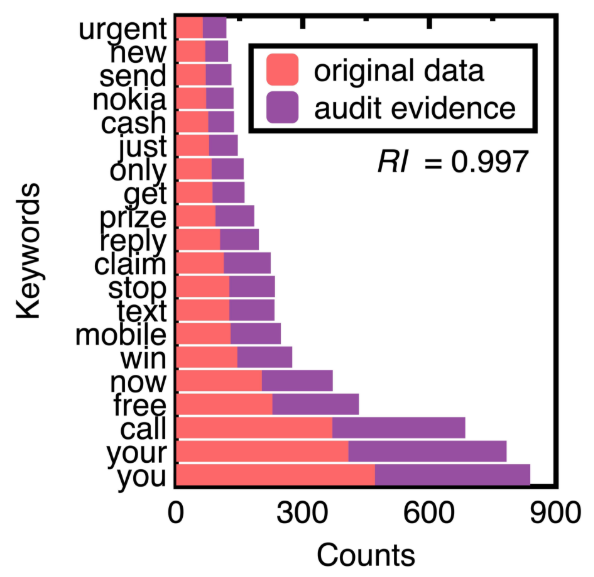
Основываясь на подсчетах ключевых слов в HAM и спам -сообщениях экспериментальных данных, рисунок 7 сравнивает 20 ключевых слов. Выбор их устраняет обычные соединения и предлоги, такие как «к» и »и. Мы можем понять уникальные ключевые слова спам -сообщений с рисунка 7.

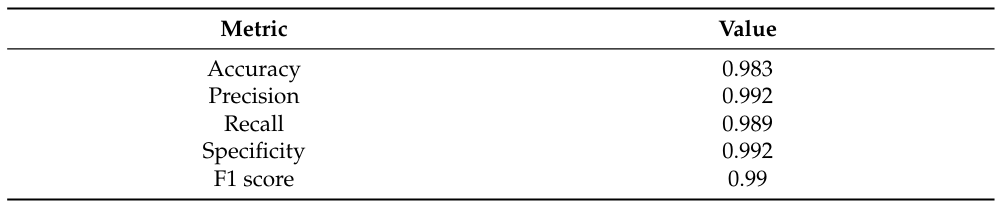
Чтобы предотвратить ошибки кадра и при приспособлении [15], рисунок 8 сравнивает соответствующие кривые ROC по сравнению с различными алгоритмами машинного обучения. Он также показывает вывод матрицы путаницы по уравнениям (3)-(4). Мы нормализовали его компоненты на основе количества тестовых данных. В таблице 2 перечислены другие показатели для демонстрации точности классификации в этой матрице путаницы.

Расчет значений AUC на рисунке 8 дает 0,989 (уравнения (3)-(4)), 0,923 (классификатор случайного леса) и 0,934 (модель опорных векторных машин с ядром радиальной базисной функции). Такие значения AUC указывают на модель опорных векторных машин, случайный лес и уравнения (3)-(4)-все это хорошие модели для предотвращения ошибок и под прикрытием; Тем не менее, производительность уравнений (3)-(4) по-прежнему является лучшей.

Затем это исследование выбирает 75 % доверительный интервал спам -сообщений для генерации аудиторских доказательств. Мы получили 652 образца спам -сообщений. На рисунке 9 сравниваются количество ключевых слов в верхних 20 оригинальных текстовых данных и аудиторских доказательств. Заменить их задние вероятности вычисления индекса репрезентативности RI равен 0,997.

Figure 9 demonstrates that machine learning integration promotes sampling unstructured data (e.g., spam messages) while keeping their crucial information. The design of conventional sampling methods does not consider unstructured data [4]. In this figure, sampling spam messages keeps the ranking of all the top 20 keywords. The resulting samples may form a benchmark data set for testing the performance of different spam message detection methods.

4.3. Эксперимент 3

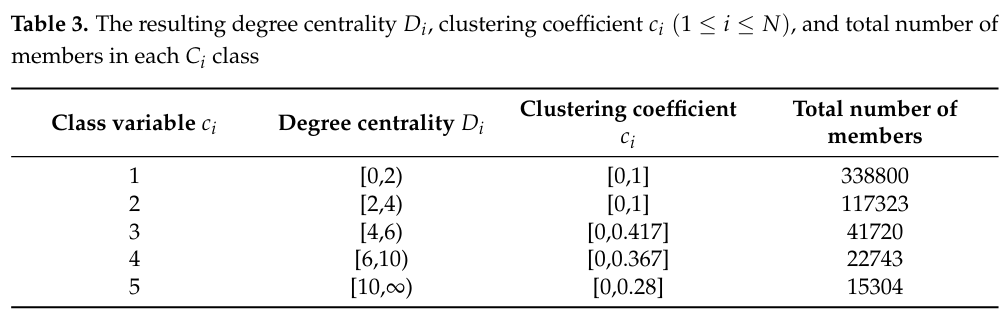
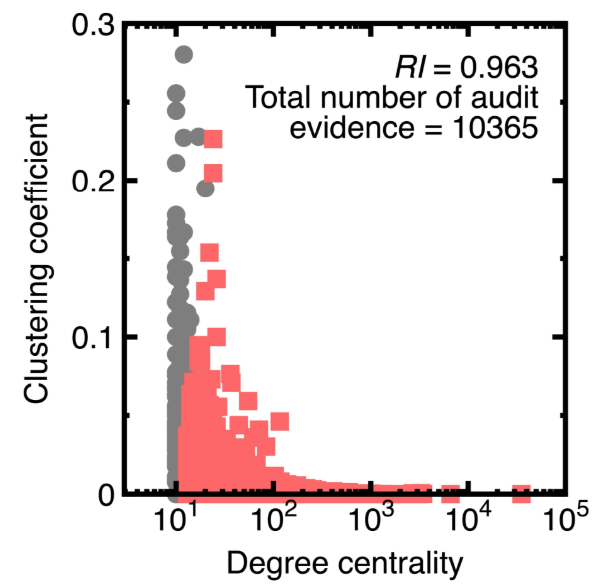
Третий эксперимент показывает, что интеграция машинного обучения с выборкой может сбалансировать репрезентативность и рискованность. Мы используем Panama Papers для создания направленной графической модели с вершинами 535891, в которых каждая вершина обозначает подозрительный финансовый счет. Его атрибуты - степень центральности и коэффициента кластеризации.

Панамские документы были огромной утечкой документов. Они разоблачили, как богатые люди, политики и общественные деятели во всем мире использовали оффшорные финансовые счета и компании Shell, чтобы уклониться от налогов, отмывать деньги и участвовать в других незаконных действиях.

Степень центральности D [17] - это количество краев, соединяющихся с вершиной. Чем выше центральная степень, тем больше возможность обнаруживает течет черных денег. Кроме того, мы считаем, что у двух финансовых счетов могут быть повторные денежные переводы. Следовательно, вычисление центральной степени учитывает существование множественных краев. Например, если отправитель передает деньги получателю получателя два раза, степень вершины, имитирующей такого отправителя или получателя, равна 2.

Между тем, коэффициент кластеризации C [17] измеряет степень, в которой узлы на графике имеют тенденцию к группе. Данные показывают, что в реальных сетях вершины могут создавать близкие группы, характеризующиеся относительно высокой плотностью связей. В проблеме отмывания денег уникальный коэффициент кластеризации может выделить группу, в которой ее члены обмениваются черными деньгами. Как и расчет центральной степени, расчет коэффициента кластеризации учитывает возможное существование множественных краев.

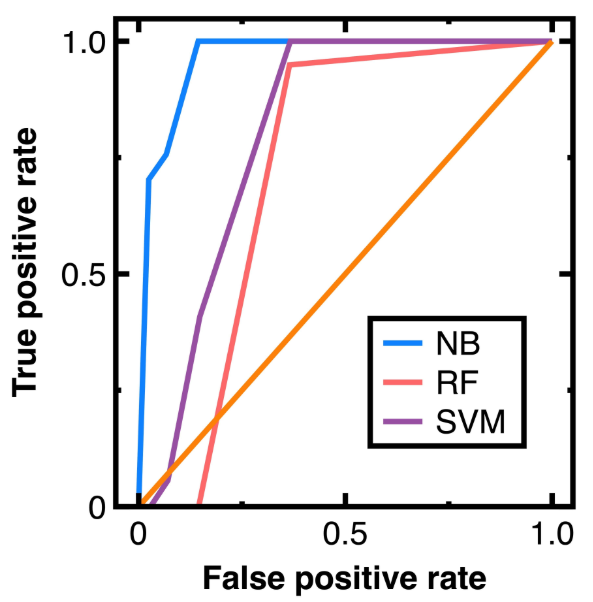
Чтобы предотвратить ошибки и при приспособлении [15], на рисунке 10 рисунок 10 сравнивается кривые ROC, выводящие различные алгоритмы машинного обучения в классификационных узлах в эксперименте 3. Получение рисунка 10 выбирает 80 % случайных узлов в качестве данных поезда и других вершин в качестве тестовых данных. Более того, уравнения (3)-(4) Вывод матрицы путаницы, показанная в уравнении (18):

в котором каждый компонент был нормализован на основе количества тестовых данных.

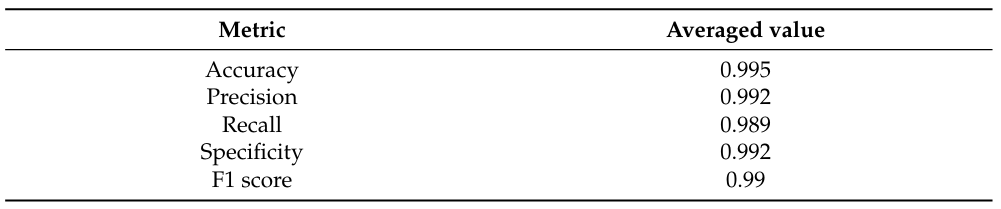
Из уравнения (18) мы дополнительно рассчитываем усредненную точность, специфичность, воспоминание, точность и значение F1, как показано в таблице 4. Далее, расчет значений AUC из рисунка 10 и таблицы 4 приводит к 0,965 (уравнения (3)-(4)), 0,844 (классификатор случайного леса) и 0,866 (модель модели Vector-Vector-Vector с функцией Radial Base FundEL). На рисунке 10 показано, что модель случайного лесного классификатора и векторных машин опорных векторов с ядром радиальной базисной функции не подходит для этого эксперимента. Поскольку в этом эксперименте мы имеем большой объем данных, эти два алгоритма могут выводить неприемлемые ошибки в узлах отбора проб.

5. Обсуждение

Раздел 4 подразумевает преимущества и ограничения интеграции наивного байеса классификатора с выборкой. Мы также перечислим эти преимущества и ограничения:

• Традиционные методы отбора проб [4] не могут профилировать полное разнообразие данных; Таким образом, они могут обеспечить предвзятые образцы. Поскольку это исследование выбирает данные после классификации их с использованием наивного классификатора Байеса, оно заменяет метод отбора проб для профилирования всего разнообразия данных. Экспериментальные результаты раздела 4 показывают, что классификатор наивного байеса точно классифицирует три открытых набора данных, даже если они чрезмерны. Эти точные результаты классификации показывают, что мы захватываем все разнообразие экспериментальных данных.

• Разработка традиционных методов выборки может не учитывать сложные закономерности или корреляции в данных [4]. В этом исследовании мы обрабатываем сложные корреляции или паттерны в данных (например, структура графика в разделе 4.3) с помощью наивного байеса классификатора. Эта конструкция смягчает смещение отбора проб, вызванное сложными шаблонами или корреляциями, если он дает точные результаты классификации.

• Раздел 4.3 указывает, что наивный классификатор Байеса хорошо работает для больших данных в проблеме отмывания денег. Он превосходит модель случайного лесного классификатора и поддержки векторных машин с ядром радиальной базисной функции при классификации массовых вершин. Таким образом, мы показываем, что эффективность выборки больших данных может быть улучшена. Можно отбрасывать моделирование мошеннических финансовых счетов мошеннических счетов без профилирования конкретных групп узлов.

• Разработка традиционных методов отбора проб рассматривает структурированные данные; Тем не менее, они изо всех сил пытались обрабатывать неструктурированные данные, такие как спам -сообщения в разделе 4.2. Мы решаем эту трудность, используя наивный классификатор Байеса перед отбором проб.

• Поскольку это исследование выбывает данные из каждого класса, классифицированного по наивному классификатору Байеса, точные результаты классификации устраняют ошибки кадра выборки и неправильные размеры выборки.

Тем не менее, это исследование также находит ограничения в интеграции машинного обучения и отбора проб. Они перечислены следующим образом:

• По -прежнему возможно, что наивный классификатор Байеса дает неточные результаты классификации. Нужно проверить точность классификации перед отбором выборки с интеграцией машинного обучения.

• В реализации Раздела 3.2 необходимы пороговые значения σj (j = 1-3). Тем не менее, мы должны проверять вариации предыдущих вероятностей определения правильных значений σj (j = 1 - 3). Они обозначают второе ограничение нашей выборки на основе машинного обучения.