
LLM против Leetcode (части 1 и 2): понимание решений алгоритмических задач с помощью трансформаторов
17 апреля 2024 г.В духе программы Механистической интерпретируемости для нейронные сети, в этом посте (и, возможно, других последующих в серии) исследуются «алгоритмы», изученные моделью преобразователя для решения узкой технической задачи — модифицированной версия проблемы Leetcode «Действительные скобки».
Хотя полезность этой задачи гораздо скромнее по объему, чем более общее предсказание следующего токена, которое вы ожидаете от LLM, это упражнение поможет нам изучить некоторые из ранних интуиций, исследовательских инструментов и общих эпистемологических методологий, обычно используемых для знать, что делают модели (и откуда мы это знаем).
:::информация Ежемесячные испытания ARENA Mechinterp оказали огромное влияние на этот пост, и оттуда придет первый набор задач. (Вам обязательно стоит ознакомиться с программой.)
:::
Структура серии:
- Выберите проблему с Leetcode в качестве задачи. (Часть 1)
- Обучите на нем минимально жизнеспособную модель Трансформера. (Часть 2)
- Изучите, чему научилась модель. (Часть 3)
- Максимальная длина входной последовательности — 40 символов.
- Чтобы сделать нашу модель небольшой для быстрых итераций.
- nesting_length ≠ 0 в конце последовательности
- Каждая длина строки одинаково вероятна.
- Каждая подстрока глубины вложенности одинаково вероятна для всех строк.
Часть 1: Проблема
Проблема с допустимыми скобками в Leetcode:
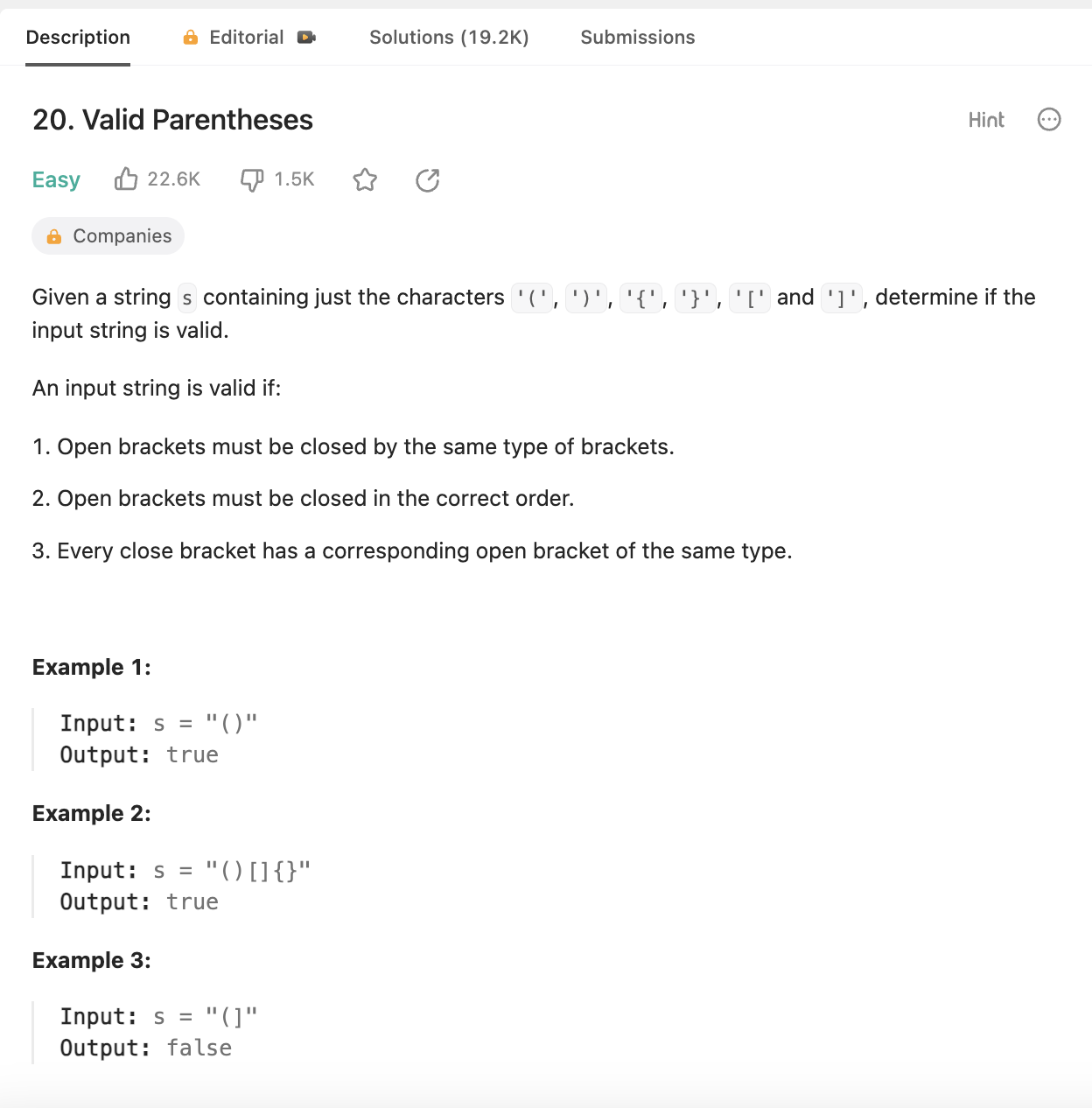
Некоторые измененные ограничения проблемы, которую мы будем использовать для этой задачи:
* Единственными допустимыми символами являются «(» и «)». * Это устраняет необходимость обрабатывать такие случаи, как "([)]".
Примеры
“(((())))” → Действительно
“()()()(” → Неверно
“)()()()(” → Неверно
Ванильное решение
def isValid(self, s: str) -> bool:
nesting_depth = 0
for bracket in s:
if bracket == '(':
# An opening bracket increases unresolved nesting depth
nesting_depth += 1
elif bracket == ')':
# A closing bracket decreases unresolved nesting depth
nesting_depth -= 1
# We don't expect to ever have negative unresolved nesting depth,
# so we can declare 'invalid' midway through the sequence if we see this
if nesting_depth < 0:
return False
# Final check that all open brackets were closed.
return nesting_depth == 0
Примечания по случаям сбоя:
“()()()((” → Неверно
При этом не очевидно, что что-то не так до самого конца, когда мы видим, что последние открытые скобки не имеют сопровождающей скобки. Следует отметить, что до самого конца в последовательности нет ни одного момента, где бы у нас было достаточно информации, чтобы понять, что что-то не так.
2. вложенность_глубина < 0 в любой точке последовательности
пример: «())()()(» → Неверно
В этом случае, с другой стороны, в третьей позиции достаточно информации, чтобы знать, что достоверность последовательности не подлежит восстановлению, поэтому мы можем объявить ее досрочным завершением.
Следует отметить, что этот пример прошел бы первый тест на отказ, поскольку nesting_length в конце был бы равен 0. Таким образом, этот тестовый пример не просто помогает нам остановиться раньше, он жизненно важен. . То же самое относится и к первому примеру случая сбоя, когда он прошел бы тест 2.
Мы не ожидаем, что модель авторегрессионного преобразователя решит проблему точно таким же образом, поскольку ее архитектура предоставляет несколько иные механизмы, чем однократный цикл последовательности и проверка, все ли в порядке. Однако мы точно знаем, что архитектура преобразователя (и другие архитектуры обработки последовательностей), по крайней мере, способна обнаруживать и обрабатывать информацию обо всех элементах последовательности. Важно помнить, что, хотя решение может выглядеть по-разному, структура проблемы одна и та же, и жесткие границы того, что известно и где в последовательности, продолжают оставаться верными, будь то цикл и операторы if или ансамбль самоопределений. - переключение внимания и нелинейности MLP.
Тогда возникает интересный вопрос: как эта архитектура использует эту информацию и легко ли ее различить с помощью существующих инструментов; потому что для достаточно производительного решения любой архитектуры неизбежно не проверять по крайней мере два вышеупомянутых случая сбоя.
Это одно из преимуществ игрушечных задач; с этими жесткими гарантиями мы получаем достаточно понятную узкую задачу, которая может помочь в расследовании, как мы скоро увидим.
Часть 2. Данные и усилители; Модель
Подготовка обучающих данных
Вот некоторые целевые характеристики, которых мы добиваемся при создании данных:
* Равное количество сбалансированных и несбалансированных струн. * Строки будут четной длины, поскольку строка нечетной длины явно несбалансирована; что было бы не очень интересной эвристикой для изучения модели. * Все длины строк (2–40) должны быть равновероятными. * Для заданной длины строки все потенциальные глубины вложения скобок должны быть равновероятными.
Очевидна общая тема: мы пытаемся сделать каждую мыслимую статистику распределения одинаково вероятной, чтобы уменьшить смещение в любом заданном направлении, обеспечить надежность и исключить очевидные эвристики быстрого выигрыша как вариант для модели. Для создания случаев сбоя мы сначала создадим действительные круглые скобки с указанными выше гарантиями, а затем изменим половину из них, чтобы они стали несбалансированными.
from random import randint, randrange, sample
from typing import List, Tuple, Union, Optional, Callable, Dict
from jaxtyping import Float, Int
import torch as t
from torch import Tensor
import plotly.express as px
import einops
from dataclasses import dataclass
import math
def isValid(s: str) -> bool:
nesting_depth = 0
for bracket in s:
if bracket == '(':
# An opening bracket increases unresolved nesting depth
nesting_depth += 1
elif bracket == ')':
# A closing bracket decreases unresolved nesting depth
nesting_depth -= 1
# We don't expect to ever have negative unresolved nesting depth,
# so we can declare 'invalid' midway through the sequence if we see this
if nesting_depth < 0:
return False
# Final check that all open brackets were closed.
return nesting_depth == 0
assert isValid('()()((((()())())))') == True
assert isValid(')()((((()())()))(') == False
Схема генерации данных №1: случайное блуждание
Первая попытка создания круглых скобок просто выполняет случайное блуждание. Но, как вы можете видеть на графиках ниже, подпространство несбалансированных круглых скобок намного больше, чем у сбалансированных; поэтому нам придется ввести стохастичность по-другому.
PARENS = ['(', ')']
def get_random_walk_parens(parens_num: int, length_range: Tuple[int]) -> List[str]:
range_start, range_end = length_range
random_parens = [
# Add 1 to make passed range_end inclusive
''.join(PARENS[randint(0, 1)] for _ in range(randrange(range_start, range_end + 1, 2)))
for _ in range(parens_num)
]
return random_parens
random_parens = get_random_walk_parens(1000, (2, 10))
random_parens[:10]
# output
[')(',
'(((())()',
')(((()()))',
'))))))',
'))())()(',
'))',
'(())',
')()(()()()',
')()())))((',
'()']
is_valid_evals = [str(isValid(random_paren)) for random_paren in random_parens]
len_evals = [len(random_paren) for random_paren in random_parens]
fig = px.histogram(is_valid_evals, title="Count of is-balanced for random walk parentheses strings")
fig.show()
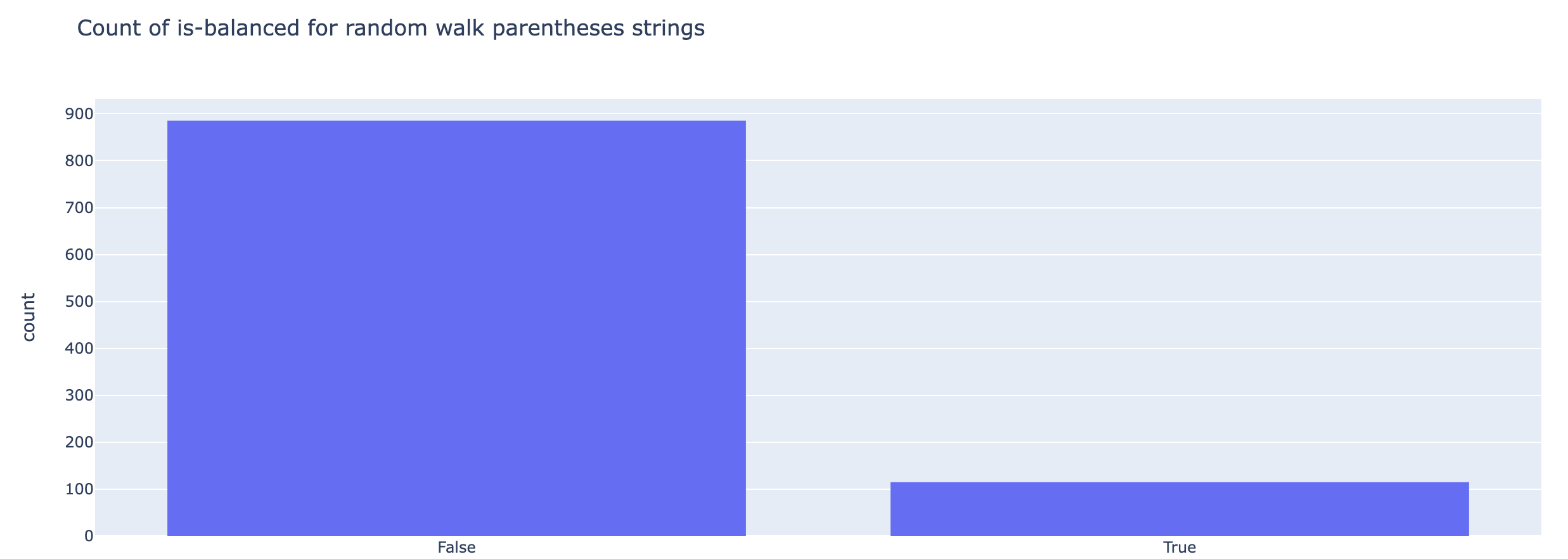
Схема генерации данных №2: жадная случайная последовательность вложений
Мы можем разбить конструкцию строки сбалансированных круглых скобок на отдельные блоки вложенных круглых скобок. Для этой жадной конструкции на каждом этапе процесса создания строки глубина вложенности выбирается из корзины возможных глубин (чтобы соответствовать целевой длине строки).
Например, для целевой длины 6 возможны следующие уникальные декомпозиции вложенности:
<код>-> [2, 1], [1, 2], [1,1,1] или [3]
Соответствует:
-> (())(), ()(()), ()()(), ((()))
def get_balanced_parens(nest_depth: int) -> str:
"""Generate parentheses at the required nesting depth."""
return (PARENS[0] * nest_depth) + (PARENS[1] * nest_depth)
assert get_balanced_parens(3) == '((()))'
def get_balanced_sequence_parens(nest_depth_sequence: List[int]) -> str:
"""Return a parentheses string following the nesting depth sequence from a given list."""
return ''.join(get_balanced_parens(nest_depth) for nest_depth in nest_depth_sequence)
assert get_balanced_sequence_parens([1,1,2,3]) == '()()(())((()))'
def get_random_depth_sequence(target_paren_len: int) -> List[int]:
depth_sequence = []
while target_paren_len > 0:
depth = randint(1, target_paren_len / 2)
depth_sequence.append(depth)
target_paren_len -= 2 * depth
return depth_sequence
rand_depth_seq = get_random_depth_sequence(10)
print(rand_depth_seq)
# Example output: '[3, 1, 1]'
assert sum([2 * depth for depth in rand_depth_seq]) == 10
def get_random_sequence_parens(parens_num: int, length_range: Tuple[int]) -> List[str]:
random_depth_sequences = [get_random_depth_sequence( randrange(*length_range, 2) ) for _ in range(parens_num)]
random_parens = [
get_balanced_sequence_parens(random_depth_sequence) for random_depth_sequence in random_depth_sequences
]
return random_parens, random_depth_sequences
Получить сбалансированные скобки
random_seq_parens, depth_sequences = get_random_sequence_parens(100000, (2, 11))
is_valid_evals = [str(isValid(random_paren)) for random_paren in random_seq_parens]
len_evals = [len(random_paren) for random_paren in random_seq_parens]
Посмотрим частоты глубины вложенности
depth_freq = {}
for seq in depth_sequences:
for depth in seq:
depth_freq.setdefault(depth, 0)
depth_freq[depth] += 1
depth_freq
# output -> {2: 39814, 1: 100088, 3: 20127, 4: 9908, 5: 4012}
depth_seq_hist = px.histogram(depth_sequences, title="Frequence of nesting depths in 'Random Nesting Depth Sequence' Output")
depth_seq_hist.show()
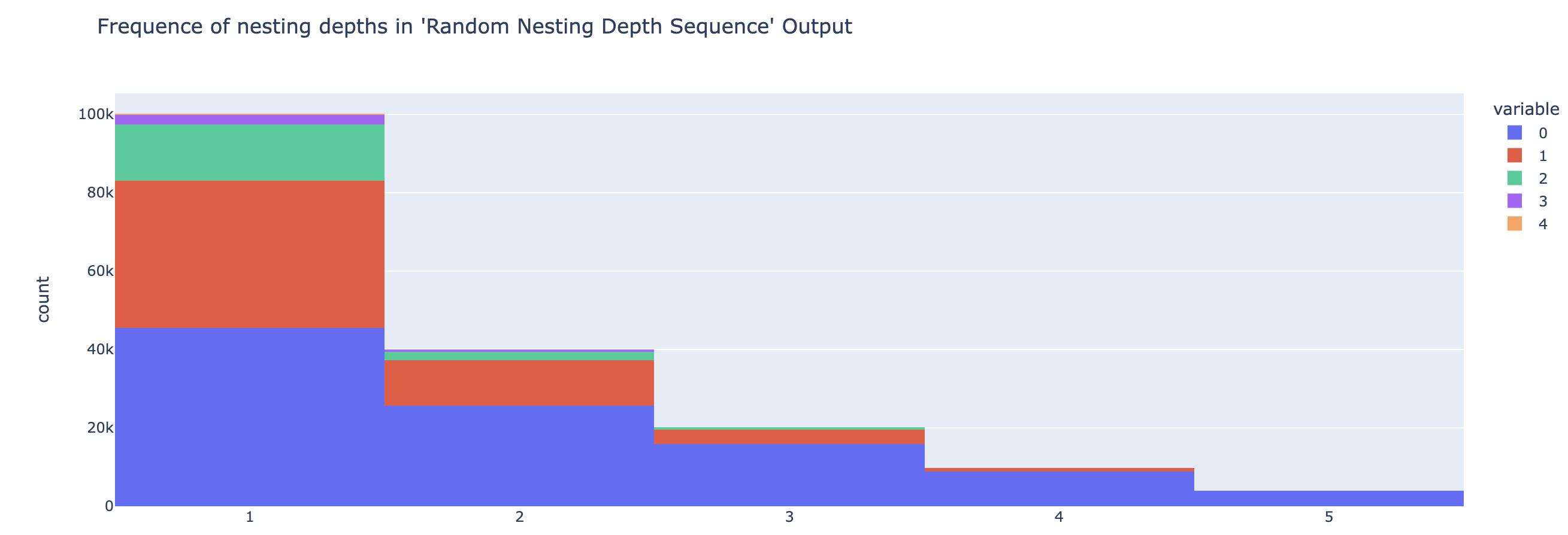
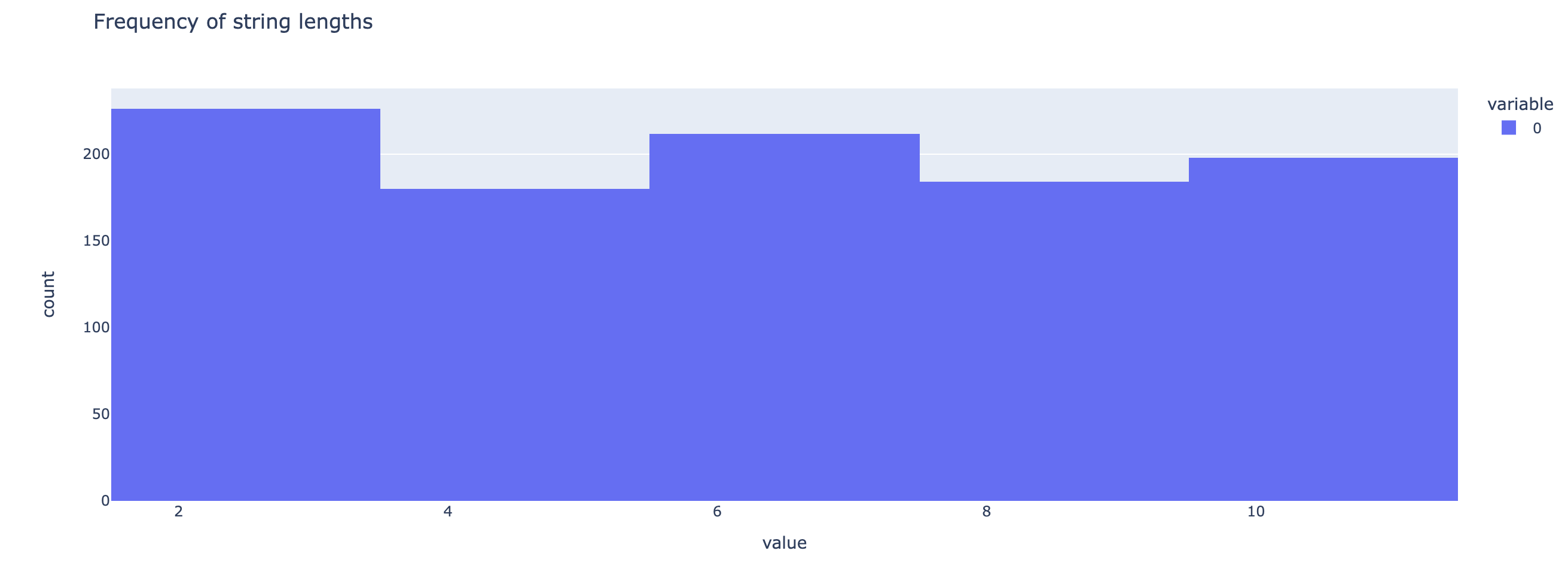
А теперь посмотрим частоты длины.
paren_len_hist = px.histogram(len_evals, title="Frequency of string lengths")
paren_len_hist.show()
Примечание по созданию данных
Обратите внимание, что существует противоречие между следующими потенциальными свойствами нашего распределения данных.
Это связано с тем, что подпоследовательности с низкой глубиной вложения будут иметь больше возможностей появиться в данной случайной последовательности вложенности, как показано на графиках выше.
Чтобы противостоять этой естественной тенденции чисто случайной последовательности, при создании заданной подстроки круглых скобок мы могли бы выполнить выборку из распределения, искаженного, чтобы повысить вероятность более глубоких значений гнезда.
К этому вопросу мы вернемся после первого прохождения обучения.
px.histogram(random_seq_parens, title="Frequency of balanced Parentheses").show()
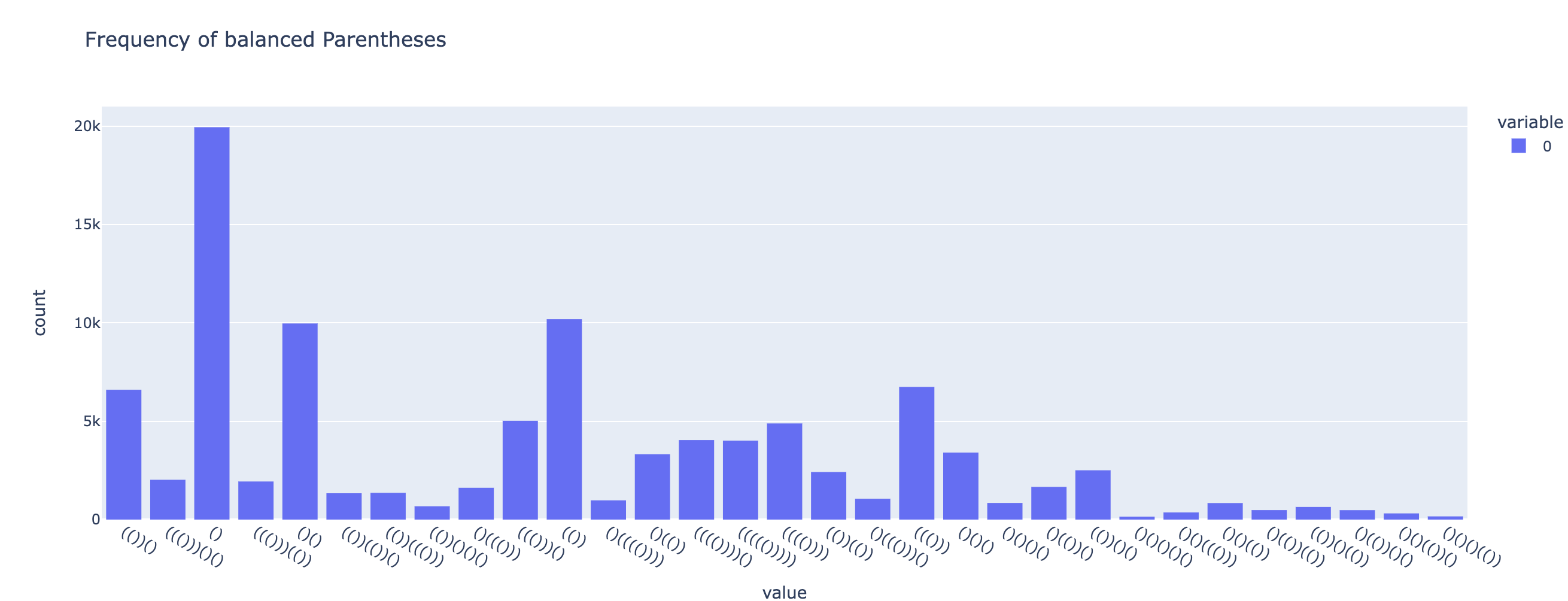
Создание несбалансированных круглых скобок
Наш набор данных не может содержать только сбалансированные круглые скобки. Таким образом, мы можем создать стратегию генерации данных для получения несбалансированных строк из нашего сбалансированного набора данных.
def _flip_idx(idx):
return (idx + 1) % 2
assert _flip_idx(0) == 1
assert _flip_idx(1) == 0
def make_parens_unbalanced(paren: str) -> str:
"""Take balanced-parentheses and randomly mutate it till it's unbalanced.
Both the number of mutations and indices are chosen at random.
"""
paren_idx_dict = {'(': 0, ')': 1}
paren_list = list(paren)
num_flipped_positions = randint(1, len(paren))
while isValid(''.join(paren_list)):
flip_points = sample(range(len(paren)), num_flipped_positions)
for flip_idx in flip_points:
idx_char = paren_idx_dict[paren_list[flip_idx]]
flipped_idx = _flip_idx(idx_char)
paren_list[flip_idx] = PARENS[flipped_idx]
return ''.join(paren_list)
assert not isValid(make_parens_unbalanced('((()))'))
Получить несбалансированный набор данных по парным элементам
unbal_random_seq_parens = [make_parens_unbalanced(paren) for paren in random_seq_parens]
Обучение модели
Теперь у нас есть наборы данных. Ради интереса мы напишем архитектуру Transformer с нуля.
Сначала немного настроек
@dataclass
class Config:
context_len = 12
d_vocab: int = 5
d_out_vocab: int = 2
d_model: int = 56
d_head = 28
d_mlp = 56 * 4
causal_attention = False
num_heads = 2
num_layers = 3
init_range: float = 1
PAD_TOKEN_IDX = 1
Затем наш токенизатор для анализа входных данных:
class Tokenizer:
def __init__(self, vocab: str, context_width: Int, enforce_context: bool=False):
self.START_TOKEN, START_TOKEN_IDX = "<start>", 0
self.PAD_TOKEN, PAD_TOKEN_IDX = "<pad>", 1
self.END_TOKEN, END_TOKEN_IDX = "<end>", 2
util_tokens_t_to_i = {self.START_TOKEN: START_TOKEN_IDX, self.PAD_TOKEN: PAD_TOKEN_IDX, self.END_TOKEN: END_TOKEN_IDX}
util_tokens_i_to_t = {START_TOKEN_IDX: self.START_TOKEN, PAD_TOKEN_IDX: self.PAD_TOKEN, END_TOKEN_IDX: self.END_TOKEN}
self.enforce_context = enforce_context
self.context_width = context_width
self.vocab = vocab
self.t_to_i = {**util_tokens_t_to_i, **{token: token_id + 3 for token_id, token in enumerate(self.vocab)}}
self.i_to_t = {**util_tokens_i_to_t, **{token_id + 3: token for token_id, token in enumerate(self.vocab)}}
@staticmethod
def pad_sequence(sequence: str, end_token: str, pad_token: str, max_length: Int, enforce_context: bool) -> List[str]:
if not enforce_context:
# Truncate if sequence length is greater
sequence = sequence[:max_length]
else:
assert len(sequence) <= max_length, f"Sequence length is greater than the max allowed data length: {max_length}"
return list(sequence) + [end_token] + [pad_token] * (max_length - len(sequence))
def tokenize(self, data: Union[str, List[str]]) -> Int[Tensor, "batch seq"]:
if isinstance(data, str):
data = [data]
def _list_tokens_to_id(tokens: List[str]) -> List[Int]:
return [self.t_to_i[token] for token in tokens]
# to leave room for start and end tokens
max_seq_len = self.context_width - 2
data_as_tokens = [
_list_tokens_to_id([
self.START_TOKEN,
*self.pad_sequence(seq, self.END_TOKEN, self.PAD_TOKEN, max_seq_len, self.enforce_context),
])
for seq in data
]
return t.tensor(data_as_tokens)
(Не)встраивания
class EmbedLayer(t.nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.W_E = t.nn.Parameter(t.empty(cfg.d_vocab, cfg.d_model))
t.nn.init.normal_(self.W_E, mean=0.0, std=cfg.init_range)
def forward(self, x: Int[Tensor, "batch seq"]) -> Int[Tensor, "batch seq d_model"]:
return self.W_E[x]
class UnEmbedLayer(t.nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.W_U = t.nn.Parameter(t.empty(cfg.d_model, cfg.d_out_vocab))
t.nn.init.normal_(self.W_U, mean=0.0, std=cfg.init_range)
def forward(self, x: Int[Tensor, "batch seq d_model"]) -> Int[Tensor, "batch seq d_out_vocab"]:
return x @ self.W_U
class PositionalEmbedding(t.nn.Module):
def __init__(self, cfg: Config):
super().__init__()
denom = t.exp(
t.arange(0, cfg.d_model, 2) * -(math.log(10000.0) / cfg.d_model)
)
pos = t.arange(0, cfg.context_len).unsqueeze(1)
param = pos * denom
P_E = t.zeros(cfg.context_len, cfg.d_model)
P_E[:, 0::2] = t.sin(param)
P_E[:, 1::2] = t.cos(param)
P_E = P_E.unsqueeze(0)
self.register_buffer("P_E", P_E)
def forward(self, x):
_batch, seq_len, d_model = x.shape
x = x + self.P_E[..., :seq_len, :d_model].requires_grad_(False)
return x
Удобный слой норм
class LayerNorm(t.nn.Module):
def __init__(self, cfg):
super().__init__()
self.scale = t.nn.Parameter(t.ones(cfg.d_model))
self.bias = t.nn.Parameter(t.zeros(cfg.d_model))
def forward(self, x):
mean = t.mean(x, dim=2, keepdim=True)
var = t.var(x, dim=2, keepdim=True, unbiased=False)
y = (x - mean) / (var + 0.00001).sqrt()
return (y * self.scale) + self.bias
И, наконец, внимание!
class AttentionLayer(t.nn.Module):
def __init__(self, cfg):
super().__init__()
self.register_buffer("IGNORE", t.tensor(-1e5, dtype=t.float32))
self.cfg = cfg
self.W_Q = t.nn.Parameter(t.empty(cfg.num_heads, cfg.d_model, cfg.d_head))
self.W_K = t.nn.Parameter(t.empty(cfg.num_heads, cfg.d_model, cfg.d_head))
self.W_V = t.nn.Parameter(t.empty(cfg.num_heads, cfg.d_model, cfg.d_head))
self.W_O = t.nn.Parameter(t.empty(cfg.num_heads, cfg.d_head, cfg.d_model))
self.b_Q = t.nn.Parameter(t.zeros(cfg.num_heads, cfg.d_head))
self.b_K = t.nn.Parameter(t.zeros(cfg.num_heads, cfg.d_head))
self.b_V = t.nn.Parameter(t.zeros(cfg.num_heads, cfg.d_head))
self.b_O = t.nn.Parameter(t.zeros(cfg.d_model))
t.nn.init.normal_(self.W_Q, mean=0.0, std=cfg.init_range)
t.nn.init.normal_(self.W_K, mean=0.0, std=cfg.init_range)
t.nn.init.normal_(self.W_V, mean=0.0, std=cfg.init_range)
t.nn.init.normal_(self.W_O, mean=0.0, std=cfg.init_range)
def forward(self, params):
#TODO: revisit implementing pad_mask with hooks
x, pad_mask = params
Q = einops.einsum(x, self.W_Q, 'b s dm, h dm dh -> b s h dh') + self.b_Q
K = einops.einsum(x, self.W_K, 'b s dm, h dm dh -> b s h dh') + self.b_K
V = einops.einsum(x, self.W_V, 'b s dm, h dm dh -> b s h dh') + self.b_V
attention_scores = einops.einsum(Q, K, 'b s_q h dh, b s_k h dh -> b h s_q s_k')
scaled_attention_scores = attention_scores / (self.cfg.d_head ** 0.5)
if self.cfg.causal_attention:
scaled_attention_scores = self.apply_causal_mask(scaled_attention_scores)
scaled_attention_scores = self.apply_padding_mask(scaled_attention_scores, pad_mask)
attention_patterns = t.nn.Softmax(dim=-1)(scaled_attention_scores)
post_attention_values = einops.einsum(
attention_patterns,
V,
'b h s_q s_k, b s_k h dh -> b s_q h dh'
)
out = einops.einsum(
post_attention_values,
self.W_O,
'b s_q h dh, h dh dm -> b s_q dm'
) + self.b_O
return out
def apply_causal_mask(self, attention_scores):
b, h, s_q, s_k = attention_scores.shape
mask = t.tril(t.ones(s_q,s_k)).bool()
return t.where(mask, attention_scores, self.IGNORE)
def apply_padding_mask(self, attention_scores, pad_mask):
return t.where(pad_mask, attention_scores, self.IGNORE)
Слои MLP
class LinearLayer(t.nn.Module):
def __init__(self, in_dim, out_dim, include_bias=True):
super().__init__()
self.include_bias = include_bias
self.W = t.nn.Parameter(t.empty(in_dim, out_dim))
t.nn.init.normal_(self.W, mean=0.0, std=cfg.init_range)
self.b = None
if include_bias:
self.b = t.zeros(out_dim)
def forward(self, x: Int[Tensor, "batch seq in_dim"]) -> Int[Tensor, "batch seq out_dim"]:
out = x @ self.W
if self.include_bias:
out = out + self.b
return out
class MLP(t.nn.Module):
def __init__(self, cfg):
super().__init__()
self.in_layer = LinearLayer(cfg.d_model, cfg.d_mlp)
self.out_layer = LinearLayer(cfg.d_mlp, cfg.d_model)
self.non_linearity = t.nn.ReLU()
def forward(self, x):
post_W_in = self.in_layer(x)
post_non_lin = self.non_linearity(post_W_in)
return self.out_layer(post_non_lin)
Соберите его в трансформатор
class TransformerBlock(t.nn.Module):
def __init__(self, cfg):
super().__init__()
self.ln1 = LayerNorm(cfg)
self.attention = AttentionLayer(cfg)
self.ln2 = LayerNorm(cfg)
self.mlp = MLP(cfg)
def forward(self, params):
x, pad_mask = params
resid_mid = self.attention((self.ln1(x), pad_mask)) + x
resid_post = self.mlp(self.ln2(resid_mid)) + resid_mid
return resid_post, pad_mask
class Transformer(t.nn.Module):
def __init__(self, cfg: Config):
super().__init__()
self.cfg = cfg
self.embed = EmbedLayer(cfg)
self.pos_embed = PositionalEmbedding(cfg)
self.final_ln = LayerNorm(cfg)
self.unembed = UnEmbedLayer(cfg)
self.blocks = t.nn.Sequential(*([TransformerBlock(cfg)] * cfg.num_layers))
def forward(self, x):
#TODO: revisit implementing pad_mask with hooks
pad_mask = self.get_pad_mask(x)
res_post_pos_embed = self.pos_embed(self.embed(x))
post_blocks, _ = self.blocks((res_post_pos_embed, pad_mask))
logits = self.unembed(self.final_ln(post_blocks))
return logits
def get_pad_mask(self, x):
batch, seq = x.shape
return einops.repeat(x != self.cfg.PAD_TOKEN_IDX, 'batch seq -> batch 1 seq_q seq', seq_q=seq)
Учебные утилиты
def cross_entropy_loss(output, targets):
log_probs = output.log_softmax(dim=-1)
predictions = log_probs[:, 0]
batch, out_dim = predictions.shape
true_output = predictions[range(batch), targets]
return -true_output.sum() / batch
def test(model, data, loss_func):
inputs, targets = data
with t.no_grad():
output = model(inputs)
loss = loss_func(output, targets)
return loss
def train(model, data, optimizer, loss_func):
inputs, targets = data
optimizer.zero_grad()
output = model(inputs)
loss = loss_func(output, targets)
loss.backward()
optimizer.step()
return loss
Конфигурация обучения
cfg = Config()
tokenizer = Tokenizer('()', 12, True)
inputs = tokenizer.tokenize([*unbal_random_seq_parens, *random_seq_parens])
targets = t.tensor([*([0] * len(unbal_random_seq_parens)), *([1] * len(random_seq_parens))])
rand_indices = t.randperm(targets.shape[0])
rand_inputs = inputs[rand_indices, :]
rand_targets = targets[rand_indices]
model = Transformer(cfg)
adamW = t.optim.AdamW(model.parameters(), lr=0.01)
Фактическое обучение
batch_size = 10000
train_size = int(0.7 * batch_size)
epochs = 15
for epoch in range(epochs):
for batch_id in range(0, rand_inputs.shape[0], batch_size):
rand_inputs_batch, rand_targets_batch = rand_inputs[batch_id : batch_id + batch_size], rand_targets[batch_id : batch_id + batch_size]
train_input, train_target = rand_inputs_batch[:train_size, :], rand_targets_batch[:train_size]
test_input, test_target = rand_inputs_batch[train_size:, :], rand_targets_batch[train_size:]
train(model, (train_input, train_target), adamW, cross_entropy_loss)
test_loss = test(model, (test_input, test_target), cross_entropy_loss)
print(f'Loss: {test_loss} on epoch: {epoch}/{epochs}')

В части 3 мы исследуем внутренности этой обученной сети. Мы сделаем это, изучив модели внимания и применив некоторые диагностические инструменты механистической интерпретируемости, такие как исправление активации, чтобы построить механистическую модель понимания того, как сеть решила эту задачу.
Спасибо, что дочитали до этого места, и скоро увидимся в третьей части!
Оригинал
