
Пределы механизмов справедливой скидки в транзакциях блокчейна
30 июня 2025 г.Таблица ссылок
Аннотация и 1. Введение
Связанная работа
Предварительные
3.1 TFMS: желательные свойства
3.2 Механизм перераспределения Groves (RM)
Идеал-TFRM: невозможность достижения строго положительного индекса перераспределения
Механизм перераспределения платы за транзакцию (TFRM)
R-TFRM: TFRM, надежный для манипуляций с шахтером
6.1 R-TFRM: анализ влияния манипуляций с шахтером на скидку и доходы от шахтеров
R2-TFRM: надежный и рациональный TFRM
Заключение и ссылки
A. Доказательства для результатов раздела 4 и 5
B. Доказательства для результатов раздела 6
C. Доказательства для результатов раздела 7
4 Идеал-TFRM: невозможность достижения строго положительного индекса перераспределения

Худшая скидка.Теорема 2 формально показывает невозможность одновременно гарантировать UIC и минимизировать комиссионные за транзакции в идеальном TFRM.
Теорема 2 (идеальная невозможность).Если 𝑟 ★-это анонимная функция скидки, которая удовлетворяет теореме 1, ни один идеальный TFRM не может гарантировать ненулевой индекс перераспределения (RI) в худшем случае.
Доказательство эскиза. Неофициально, если функция скидки является анонимной (определение 7), а пользователь с высочайшей ценной транзакцией подтверждается и получает положительную скидку. Затем легко показать, что существует другой профиль ставки, для которого последняя неподтвержденная транзакция должна получить одинаковую положительную скидку. Следовательно, единственный способ обеспечить нулевую скидку для неподтвержденных транзакций - это также обеспечить нулевую скидку для каждой подтвержденной транзакции. Таким образом, худший случай RI равен нулю. См. Приложение A.1 для официального доказательства.

Детали обучения.Мы сохраняем 𝑛 = 10 с количеством подтвержденных транзакций как 𝑘 = 7. Для оптимизатора мы выбираем фиксированную скорость обучения 𝜂 = 5𝑒 - 4. Размер партии составляет 1000, и мы тренируемся на 50 000 эпох.
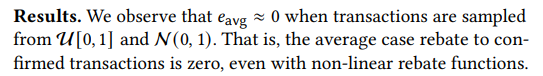
Мы пришли к выводу, что невозможно спроектировать TFRM с линейной функцией скидок, которая является UIC (теорема 1) и предлагает ненулевую скидку любому агенту. Наши эксперименты также подчеркивают, что это также может быть маловероятным для нелинейных функций скидок. Таким образом, в следующем разделе представлена общая структура TFRM, где мы сосредотачиваемся на ограниченном UIC.
5 Механизм перераспределения платы за транзакцию (TFRM)

TFRM: Ruic.Хотя функция скидок удовлетворяет теореме 1, обратите внимание, что TFRM не UIC. Например, пользователи, не являющиеся частью блока, могут сообщать 𝑏> 𝜃 для захвата дополнительной скидки, поскольку только подтвержденные заявки платят плату за транзакцию. Тем не менее, TFRM удовлетворяет RUIC, то есть, это является UIC для агентов, включенных в блок, чтобы предложить их истинную оценку. Все включенные пользователи, подтвержденные или нет, предлагаются скидки, подразумевая, что 𝑘 слоты, предлагаемые пользователям, эквивалентны распределению ресурсов среди агентов. Таким образом, по теореме 1, TFRM является RUIC
Теперь мы показываем, что в присутствии стратегического майнера TFRM на рисунке 2 приводит к скидкам NET Zero для подтвержденных пользователей.

Таким образом, проектирование TFRM для минимизации сборов за транзакцию может работать только в том случае, если она станет устойчивой к таким стратегическим манипуляциям. В отличие от RMS, TFRM должны количественно оценить перераспределенную скидку на подлинных пользователей. На пути к этому мы определяем следующий показатель:

Авторы:
(1) Sankarshan Damle, IIIT, Хайдарабад, Хайдербад, Индия (Sankarshan.damle@research.iiit.ac.in);
(2) Маниша Падала, IISC, Бангалор, Бангалор, Индия (manishap@iisc.ac.in);
(3) Суджит Гуджар, IIIT, Хайдарабад, Хайдербад, Индия (sujit.gujar@iiit.ac.in).
Эта статья есть
[4] Присвоение будущих затрат на транзакции не подтверждено, например, как в [8] (раздел 2), может помочь преодолеть такие манипуляции. Мы оставляем анализ для будущей работы.
Оригинал
