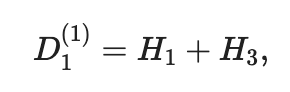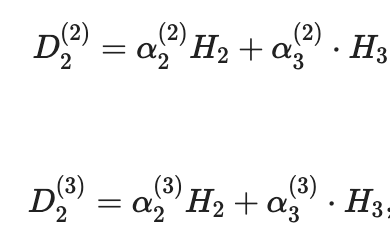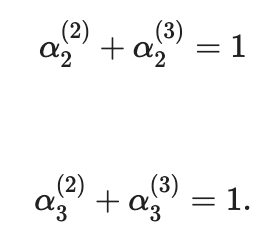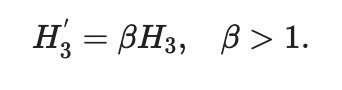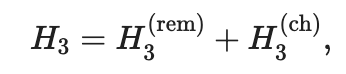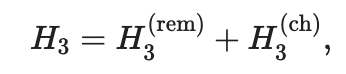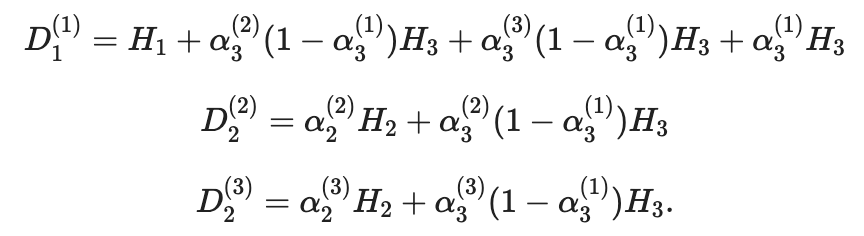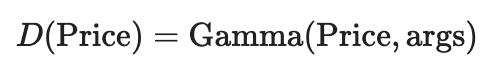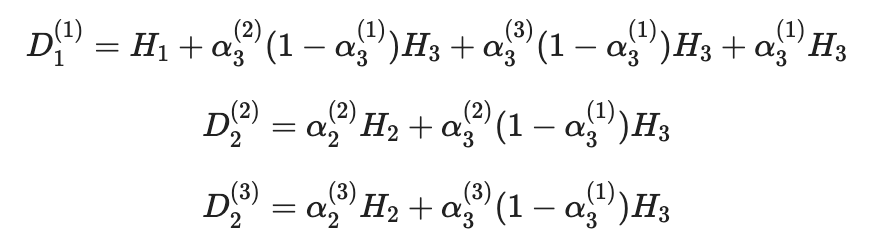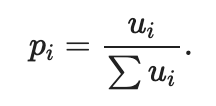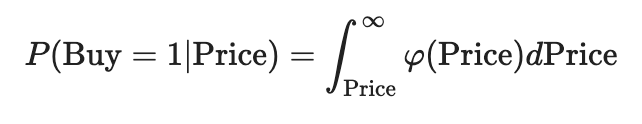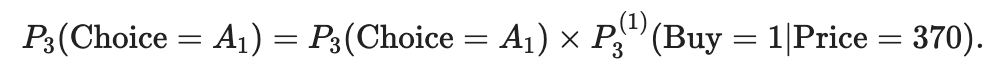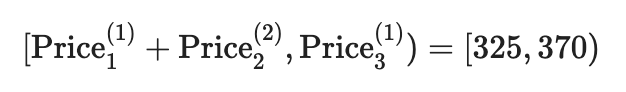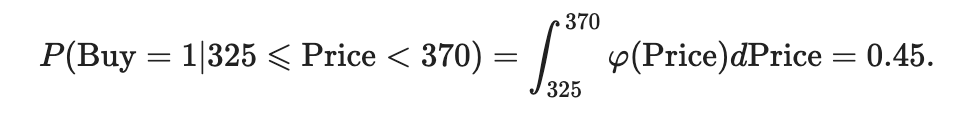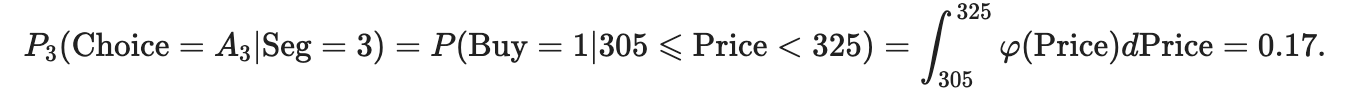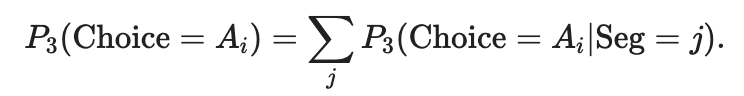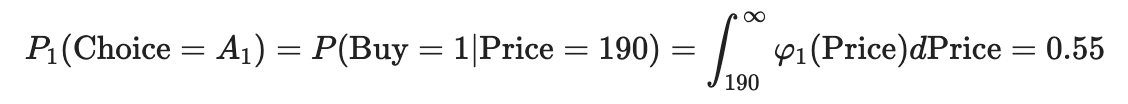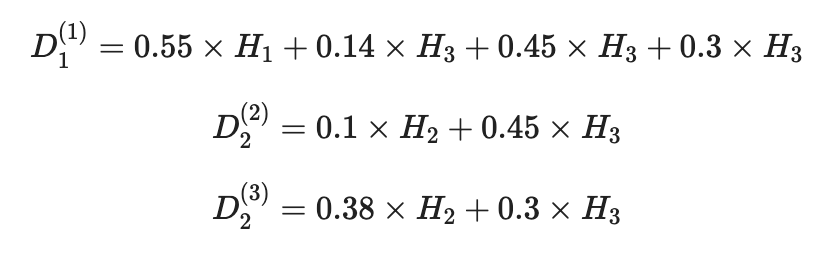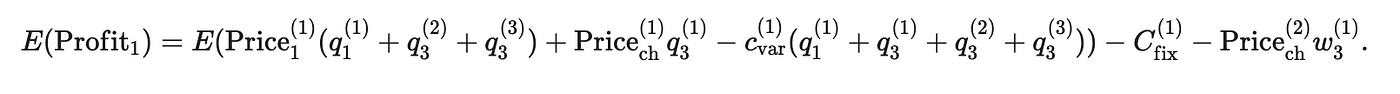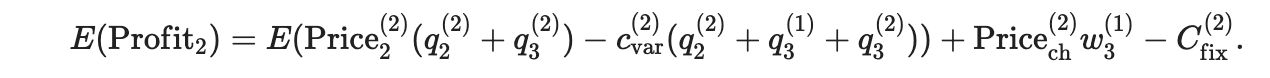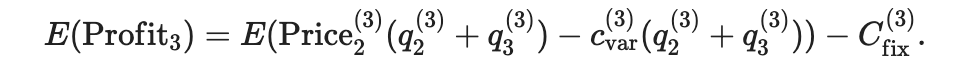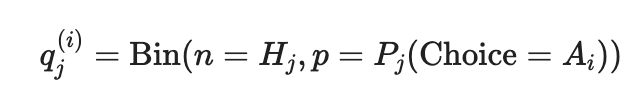Как ваше время укладки может сделать или сломать прибыль авиакомпании

Когда реальность не соответствует ожиданиям, она всегда неприятна. Это особенно неприятно, если вы заплатили деньги за ожидаемую реальность: вы покупаете билет в одной авиакомпании, но по какой -то причине вы садитесь на самолет совершенно другой авиакомпании. Затем вы устанавливаете соединение, и они поставили вас на плоскость какой -то неизвестной третьей авиакомпании. Что происходит? В конце концов, у вас есть билет в авиакомпании, который вы купили только потому, что вы знаете, чего от нее ожидать, но вы все еще летите с самолетами совершенно разных авиакомпаний. Похоже, вы купили билет у большой и устоявшейся авиакомпании, но на борту оказывается, что в этой авиакомпании есть региональные дочерние компании и филиалы, которые не так хороши. Первое знакомство с рейсами Codeshare может быть очень неприятным.

Разве авиакомпании не понимают, что такие действия могут заставить путешественников полностью изменить свои предпочтения? Негативный опыт быстро создает навык, чтобы использовать более тщательный подход к оценке возможных альтернатив. Пассажирские потоки похожи на жидкость, которая течет в большем объеме, где на его пути меньше препятствий. В этом случае даже небольшая разница в оценках авиакомпаний и путешественников в отношении привлекательности полетов может привести к значительному отвлечению пассажирских потоков.

Снижение привлекательности полета одной авиакомпании приводит к так называемому «розливу» части пассажирского потока. Другая авиакомпания может забрать разлив, предложив более привлекательную альтернативу - взяв на себя захват. Такая модель называется моделью разлива и захвата (захват) пассажирского потока и непосредственно связывает прибыль авиакомпании с положительным опытом путешественника. Эта статья посвящена тому, как сделать рейсы Codeshare более привлекательными, и получить хорошую прибыль на нее (конечно, не оставляя своих конкурентов).

Распределение пассажира

Давайте сразу же приступим к проблеме. Предположим, есть небольшая маршрутная сеть из трех городов, состоящая только из трех маршрутов:

• A → B - рейсы управляются A1;
• B → C - рейсы управляются A2 и A3;
• A → B → C - в первом сегменте рейсы управляются A1, на втором A2 и 3 - это маршрут, который требует оценки оптимальности соглашения об кодешке.

Пассажирские потоки могут быть представлены в двух формах - давайте назовем их H и D:

• H - элементарный пассажирский трафик между двумя городами;
• D - Композитный пассажирский трафик между двумя городами.

Например, в сегменте A → B авиакомпания A1 может оценить (наблюдать, меньше, чем емкость) пассажирский поток D11, который представляет собой сумму двух элементарных пассажирских потоков:

где верхний индекс в скобках соответствует номеру авиакомпании. В этом случае H1 - это пассажирский поток путешественников, заинтересованных в добе до B до B, а H3 - это пассажирский поток путешественников, заинтересованных в добрах от A до C.

Для сегмента B → C все немного интереснее:

где α можно интерпретировать как доля авиакомпании элементарного пассажирского трафика. В этом случае авиакомпании A2 и A3 разделяют пассажирские трафики H2 - путешественники, переходящие от B до C, и пассажирский трафик H3 - путешественники, переходящие от A в C и соединяющиеся в аэропорту города B.

Параметр α также можно интерпретировать как вероятность совершения покупки билета на конкретном полете авиакомпании, поэтому:

α зависит от привлекательности рейсов и определяется функцией полезности U (R), где R является вектором параметров полета, в зависимости от того, какие путешественники решают купить билет. Как правило, экспоненты функции используются в качестве функции утилиты и преобразуются в вероятности с использованием функций Soft-Max. Это хороший способ сделать это? Это распространено и просто. В то же время, сигмоидные функции и функция распределения Dirichlet гораздо лучше вписываются в парадигму голосования. Например, если бы проводился опрос путешественников, в котором вам приходилось оценить каждый параметр полета по 10-балльной шкале, именно бета и дирихлевые распределения обработали бы результаты. Это сложнее, но дает больше результатов.

Влияние соглашений о кодешнике на привлекательность маршрута

Полеты кодов привлекательны для путешественников, потому что они позволяют пассажирам:

• Накапливайте бонусные мили, участвуя в программе лояльности авиабилии, даже если рейс управляется другим перевозчиком.
• Забронируйте билеты на воздушные билеты на рейсы с удобными соединениями, выбирая наиболее подходящий вариант среди предложений различных авиакомпаний.
• Получите помощь и поддержку от авианосца во время полета независимо от компании, из которой был приобретен билет.

Тем не менее, основная причина, по которой рейсы Codeshare привлекательны, заключается в том, что они увеличивают количество маршрутов-гораздо проще выбрать готовый маршрут, чем создавать его самостоятельно. Некоторые авиакомпании прекрасно понимают, что привлекательность полетов Codeshare может быть увеличена еще больше - например, благодаря удобным факторам времени, поэтому они координируют свои графики.

Естественно, рейсы Codeshare также могут быть непривлекательными по ряду причин:

• неуместные уровни обслуживания;
• различные правила багажа и ручной клади;
• Возможность проблем багажа во время соединений.

Увеличение привлекательности полета в коде может увеличить пассажирский трафик:

Кажется, это суть вопроса, но это немного сложнее и гораздо интереснее. Теоретически, рейсы Codeshare могут увеличить общий пассажирский трафик, но в гораздо большей степени они просто увеличивают спрос.

Добавление полета в кодешке сталкивается с тремя альтернативами.

1. Летать от A до C на полете кода с минимальными неудобствами.
2. Летите от A до C через B с удобным подключением к полету авиакомпании A2.
3. Летите от A до C через B с неудобным соединением на полете Airline A3.

Предположим, это так, тогда H3 может быть представлен в качестве следующей суммы:

где h (ch) 3-путешественники, которые выбрали полет кодша и H (rem) 3-это путешественники, которые выбрали самоотдачу маршрута. H3 также должен быть разделен в некоторой пропорции:

Тогда полное перераспределение всех потоков между авиакомпаниями может быть записано в следующей форме:

Тот факт, что привлекательность маршрутов может изменить целые пассажирские потоки, может показаться довольно странным. Тем не менее, важно понимать, что мы говорим о частях пассажирских потоков, то есть отдельных сегментах путешественников, которые по -разному оценивают и оценивают возможные альтернативы. Для некоторой части путешественников утешится первым, для другой части - цены.

Спрос показывает, как цена влияет на количество приобретенных билетов. Привлекательность, с другой стороны, показывает, как на это число влияет другие факторы. Привлекательность часто фиксируется - например, для запланированных рейсов, которые не могут изменить свое время прибытия или отъезда. После того, как совместный рейс с другой авиакомпанией будет добавлен в такой рейс, время подключения может измениться, что означает, что некоторая часть путешественников будет руководствоваться более чем просто ценой при покупке билета.

Разливать и захватить

Мы получили выражение, описывающее пропорциональное изменение объемов пассажиров между авиакомпаниями. Остается выяснить, как рассчитать пропорции на основе α. Это может показаться очень сложным - в этом случае мы всегда прибегаем к простым приближениям. Мы сделаем два важных предположения:

1. У нас есть данные.
2. Мы можем создавать модели данных.

По сути, мы просто говорим о том, что мы «знаем, как делать в ML (машинное обучение)».

Во -первых, нам нужно указать случайные объемы пассажиров, состоящие из потенциальных покупателей, а именно любого, кто каким -либо образом заинтересован в покупке билета на некоторых рассматриваемых маршрутах. Лучшим кандидатом на распределение числа потенциальных покупателей является распределение Пуассона:

• H1-POISSON (λ1);
• H2-POISSON (λ2);
• H32poisson (λ3).

Давайте рассмотрим, как бутылка и захват пассажирского движения происходит с использованием примера H3, потому что этот пассажирский трафик делится между тремя авиакомпаниями. Различные уровни привлекательности полета генерируют различные уровни внимания в разных сегментах цен на пассажир. Например, полет Codeshare будет наиболее привлекательным, но по той же причине он будет самым дорогим. Это означает, что это будет интересно для тех, кто готов заплатить больше, чем обычно за билет.

Пусть привлекательность определяется двумя факторами: кодшар и время подключения.

Существует некоторое оптимальное время передачи - давайте обозначим его t ∗. Давайте предположим, что t (2) время передачи для полета A2 намного ближе к t ∗, чем t (3) - время передачи для полета A3.

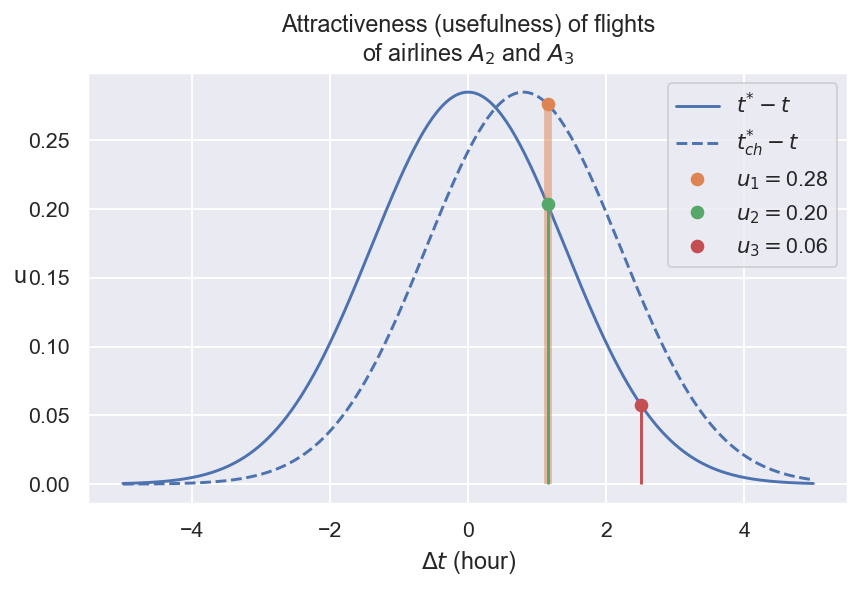
Теперь мы можем определить привлекательность (полезность двух рейсов) с помощью простой колоколообразной функции. Давайте рассмотрим три варианта:

• ΔT ∗ = t ∗ −T = 0 - минимальная разница от идеального времени передачи.
• Δt ∗ = t ∗ −t> 0 - вы должны поторопиться.
• Δt ∗ = t ∗ −t <0 - вам нужно подождать.

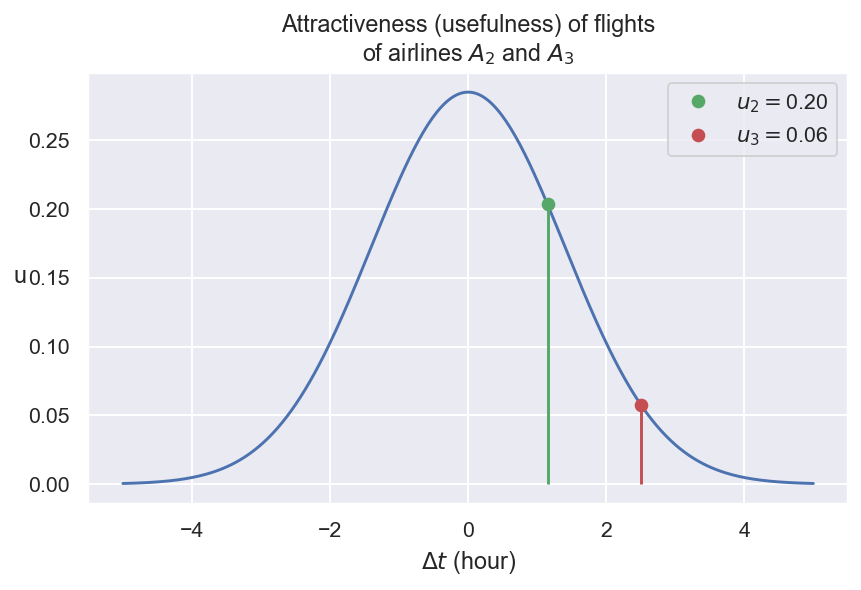
Давайте выразим достопримечательности с помощью полезных функций: U2 = U (ΔT2) и U3 = U (ΔT3), где U может быть любой унимодальной функцией: в нашем случае U является гауссовой функцией.

Привлекательность полетов A2 и A3 может быть отображена следующим образом:

Импорт Numpy As np из Scipy.stats Import Norm, Gamma, Poisson, Binom, Uniform, Bernoulli import matplotlib.pyplot как plt из pylab import rcparams rcparams ['figure.figsize'] = 7, 4 rcparams ['figure.dpi'] = 140 %inlinebled.ffeed. как sns sns.set () dt = np.linspace (-5, 5, 300) u = norm.pdf (dt, loc = 0, scale = 1,4)

plt.plot (dt, u, 'c0')

dt_2 = 1.15 u_2 = norm.pdf (dt_2, loc = 0, scale = 1.4) plt.plot (dt_2, u_2, 'c2o', label = r '$ u_ {2} = $' + f '{u_2: .2f}') plt.vlines (dt_2, 0, u_2: .2f} ')

dt_3 = 2,5 u_3 = norm.pdf (dt_3, loc = 0, scale = 1.4) plt.plot (dt_3, u_3, 'c3o', label = r '$ u_ {3} = $' + f '{u_3: .2f}') plt.vlines (dt_3, 0, u_3,.

plt.title ('привлекательность (полезность) полетов \ n' + r'of airlines $ a_ {2} $ и $ a_ {3} $ ') plt.xlabel (r' $ \ delta t $ (час) ') plt.ylabel (' u ', rowtation = 0) plt.legend () plt.show ()

Если авиакомпания A1 заключает соглашение о кодешке с A2, то, с точки зрения времени передачи, привлекательность полета Codeshare будет такой же, как у A2, поскольку идеальное время передачи - T ∗, относительно которого рассчитываются все Deltas, не изменилось. Тем не менее, рейсы Codeshare предлагают ряд преимуществ: нет необходимости перепроверить багаж, не нужно перепроверить, и для международных рейсов, оставление в четкой зоне не означает дополнительного паспортного контроля. Привлекательность полета в кодешнике увеличивается из -за того, что у путешественника меньше риска для удовлетворения ΔT2, а также есть дополнительное время, чтобы вытянуть ноги и отдохнуть от полета. Оказывается, что идеальное время подключения для полета в коде, t ∗ ch, все еще отличается от идеального времени подключения для обычного полета.

Идеальное время подключения должно учитывать несколько факторов:

• Минимальное время подключения - время, необходимое для успешного перевода пассажиров и перевода багажа с одного рейса в другой в аэропорту.
• Дополнительное время комфорта-необходимо для снижения риска бега для регистрации для другого рейса.
• Среднее время задержек полета - существует специальная статистика для каждой авиакомпании.

Идеальное время подключения для полета в кодексе уменьшится, по крайней мере, из -за того, что авиакомпания опаздывает риск, когда пассажир опаздывает на полете во время подключения, - теперь он гарантирует, что даже если путешественник опаздывает, он все равно будет поставлен на следующий рейс.

Предполагая, что t ∗ ch <t ∗, это просто приводит к сдвигу графика функции утилиты для полета A1 Codeshare A1:

dt = np.linspace (-5, 5, 300) u = norm.pdf (dt, loc = 0, scale = 1,4)

plt.plot (dt, u, 'c0', label = r '$ t^{*} - t $')

dt = np.linspace (-5, 5, 300) u_ch = norm.pdf (dt, loc = 0,8, scale = 1,4) plt.plot (dt, u_ch, 'c0--', label = r '$ t^{*} _ {ch}-t $')

dt_1 = 1.15 u_1 = norm.pdf (dt_1, loc = 0,8, scale = 1,4) plt.plot (dt_1, u_1, 'c1o', label = r '$ u_ {1} = $' + f '{u_1: .2f}') plt.vlines (dt_1, 0, u_1: .2f} '). альфа = 0,5)

dt_2 = 1.15 u_2 = norm.pdf (dt_2, loc = 0, scale = 1.4) plt.plot (dt_2, u_2, 'c2o', label = r '$ u_ {2} = $' + f '{u_2: .2f}') plt.vlines (dt_2, 0, u_2: .2f} ')

dt_3 = 2,5 u_3 = norm.pdf (dt_3, loc = 0, scale = 1.4) plt.plot (dt_3, u_3, 'c3o', label = r '$ u_ {3} = $' + f '{u_3: .2f}') plt.vlines (dt_3, 0, u_3,.

plt.title ('привлекательность (полезность) полетов \ n' + r'of airlines $ a_ {2} $ и $ a_ {3} $ ') plt.xlabel (r' $ \ delta t $ (час) ') plt.ylabel (' u ', rowtation = 0) plt.legend () plt.show ()

Если ранее разница в идеальном времени подключения составляла около 1 часа и 10 минут, для полета в коде это разница будет всего 20 минут. Естественно, приближение к идеальному времени подключения является не единственным фактором, влияющим на привлекательность (полезность) полета. Время передачи принимается только для иллюстративных целей. В действительности, расчет привлекательности основан на гораздо других факторах и выполняется инструментами ML.

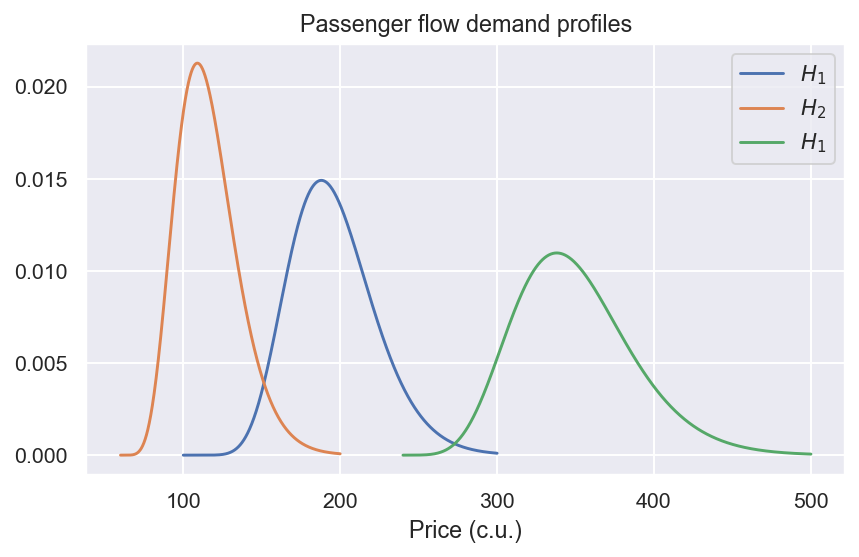
Теперь нам нужно понять, как эти три значения делят пассажирский трафик на сегменты цен - мы явно говорим о некоторых фракциях. Чтобы определить эти фракции, нам нужен профиль потенциального спроса. Давайте предположим, что для каждого из пассажирских потоков это выглядит следующим образом:

Цены_1 = np.linspace (100, 300, 1000) rvdem_1 = гамма (a = 12, loc = 100, scale = 8) profile_1 = rvdem_1.pdf (цены_1) plt.plot (цены_1, профиль_1, label = r '$ h_ {1} $')

Цены_2 = np.linspace (60, 200, 1000) rvdem_2 = гамма (a = 8, loc = 60, scale = 7) profile_2 = rvdem_2.pdf (цены_2) plt.plot (цены_2, профиль_2, label = r '$ h_ {2} $')

Цены_3 = np.linspace (240, 500, 1000) rvdem_3 = гамма (a = 10, loc = 230, scale = 12) profile_3 = rvdem_3.pdf (цены_3) plt.plot (цены_3, профиль_3, label = r '$ h_ {1} $')

plt.legend () plt.xlabel ('price (c.u.)') plt.title ('профили спроса на пассажирский поток');

Существование профиля спроса указывает на то, что существует надежное представление по каким ценам, вероятность покупки билета отличается от 0 или 1 и от того, как это зависит от цены. Следует немедленно отметить, что существование таких ценных профилей не позволяет рационально демонстрировать старые или неоптимальные практики. Во -первых, как только кто -то знаком с методами ML, довольно сложно представить, как можно сделать что -то по -другому, а тем более делать это хуже. Во -вторых, существует как минимум несколько методологий для «прогнозирования» количества билетов, продаваемых по какой -то цене. Различные авиакомпании могут использовать разные. Некоторые, как правило, небольшие авиакомпании могут полностью полагаться на интуицию. На данный момент давайте просто предположим, что в худшем случае профили спроса будут грубыми шагами.

Различные степени привлекательности альтернатив должны каким -то образом разделить пассажирские потоки между авиакомпаниями, и теперь у нас есть все, что нам нужно, чтобы рассчитать α для каждого из них:

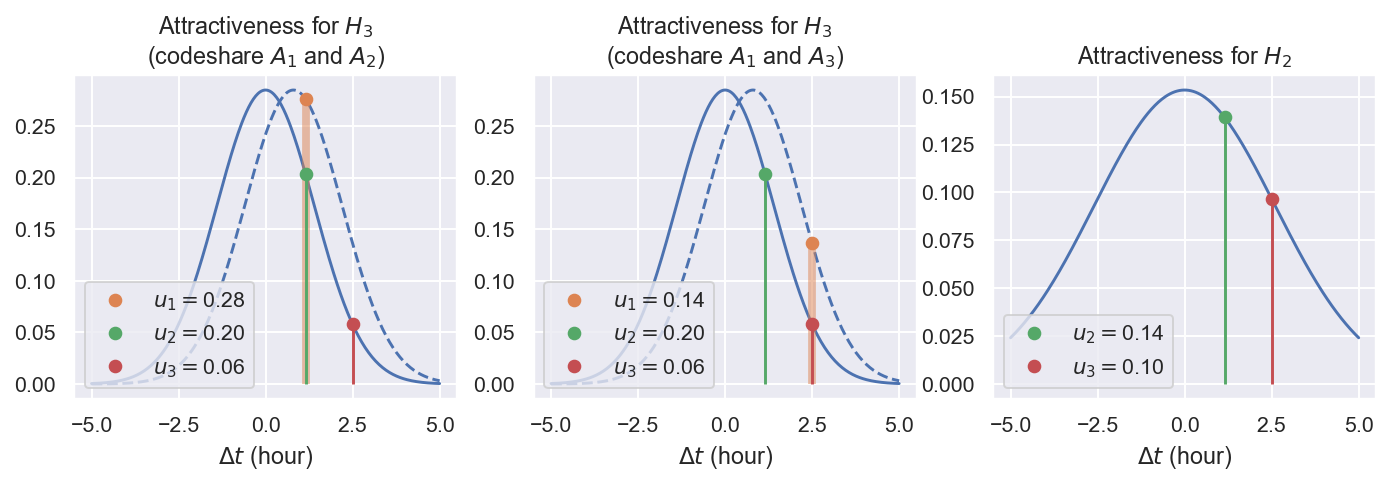
Поток H1 между авиакомпаниями не разделен. Только потоки H2 и H3 делятся, а разделение зависит от привлекательности полетов, что влияет на вероятность выбора. Привлекательность может выглядеть следующим образом:

Рис., AX = PLT.Subplots (1, 3, FigSize = (12, 3))

dt = np.linspace (-5, 5, 300) u = norm.pdf (dt, loc = 0, scale = 1,4) ax [0] .plot (dt, u, 'c0')

dt = np.linspace (-5, 5, 300) u_ch = norm.pdf (dt, loc = 0,8, scale = 1,4) ax [0] .plot (dt, u_ch, 'c0--') ax [1] .plot (dt, u_ch, 'c0--)

dt_1 = 1.15 u_1 = norm.pdf (dt_1, loc = 0,8, scale = 1,4) ax [0] .plot (dt_1, u_1, 'c1o', label = r '$ u_ {1} = $' + f '{u_1: .2f}') ax [0] .vlines (dt_1, 'u_1,',. LW = 4, альфа = 0,5)

dt_2 = 1.15 u_2 = norm.pdf (dt_2, loc = 0, scale = 1.4) ax [0] .plot (dt_2, u_2, 'c2o', label = r '$ u_ {2} = $' + f '{u_2: .2f}') ax [0].

dt_3 = 2,5 u_3 = norm.pdf (dt_3, loc = 0, scale = 1,4) ax [0] .plot (dt_3, u_3, 'c3o', label = r '$ u_ {3} = $' + f '{u_3: .2f}') [0].

ax [0] .legend (loc = 3) ax [0] .set_title ('привлекательность для $ h_3 $ \ n (codeshare $ a_ {1} $ и $ a_ {2} $)') ax [0] .set_xlabel (r '$ \ delta t $ (час)').

ax [1] .plot (dt, u, 'c0')

dt_1 = 2,5 u_1 = norm.pdf (dt_1, loc = 0,8, scale = 1,4) ax [1] .plot (dt_1, u_1, 'c1o', label = r '$ u_ {1} = $' + f '{u_1: .2f}') ax [1]. LW = 4, альфа = 0,5)

dt_2 = 1.15 u_2 = norm.pdf (dt_2, loc = 0, scale = 1,4) ax [1] .plot (dt_2, u_2, 'c2o', label = r '$ u_ {2} = $' + f '{u_2: .2f}') [1].

dt_3 = 2,5 u_3 = norm.pdf (dt_3, loc = 0, scale = 1,4) ax [1] .plot (dt_3, u_3, 'c3o', label = r '$ u_ {3} = $' + f '{u_3: .2f}') [1].

ax [1] .legend (loc = 3) ax [1] .set_title ('привлекательность для $ h_3 $ \ n (codeshare $ a_ {1} $ и $ a_ {3} $)') ax [1] .set_xlabel (r '$ \ delta t $ (час)').

dt = np.linspace (-5, 5, 300) u = norm.pdf (dt, loc = 0, scale = 2,6)

plt.plot (dt, u, 'c0')

dt_2 = 1.15 u_2 = norm.pdf (dt_2, loc = 0, scale = 2,6) ax [2] .plot (dt_2, u_2, 'c2o', label = r '$ u_ {2} = $' + f '{u_2: .2f}') ax [2].

dt_3 = 2,5 u_3 = norm.pdf (dt_3, loc = 0, scale = 2,6) ax [2] .plot (dt_3, u_3, 'c3o', label = r '$ u_ {3} = $' + f '{u_3: .2f}') [2]. ax [2] .legend (loc = 3) ax [2] .set_title ('привлекательность для $ h_2 $') ax [2] .set_xlabel (r '$ \ delta t $ (час)');

Самый простой способ преобразования утилит в вероятности - это умножить каждое из значений, чтобы результирующая сумма равна 1:

Например, если A1 заключается в соглашении о кодешке с A2, вероятности выбора одного или другого полета следующие:

u = np.array ([0,28, 0,20, 0,06])

print (u / u.sum ()) [0,51851852 0,37037037 0,11111111]

• P3 (выбор = a1 | seg = 1) = 0,52;
• P3 (выбор = a2 | seg = 1) = 0,37;
• P3 (выбор = A3 | SEG = 1) = 0,11.

Тем не менее, на выбор влияет не только предпочтения, но и на сумму денег, доступную для этого. Зная профили спроса, мы можем определить вероятность покупки билета по определенной цене. Пусть цены будут следующими:

• Цена (1) 1 = 190
• Цена (1) 3 = 370
• Цена (2) 2 = 135
• Цена (3) 2 = 115

Тогда вероятность покупки билета по какой -то цене может быть определена следующим образом:

Например, вероятность того, что билет на рейс Codeshare будет куплен по телефону 370 C.U. будет равен 0,27:

rvdem_3 = гамма (a = 10, loc = 230, scale = 12) print (rvdem_3.sf (370))

0,2727250812333501

Путешественники, которые могут позволить себе билет по этой цене, видят три альтернативы перед ними. Однако, если человек может позволить себе максимальный комфорт, это не означает, что он или она обязательно будут использовать его. Доступность более дешевых альтернатив позволяет сэкономить деньги - поэтому мы рассчитали привлекательность альтернатив и определили вероятности выбора на основе их. Общая вероятность выбора будет равна:

Полученные вероятности выбора конкретного рейса для таких пассажиров будут равны:

• P3 (выбор = a1 | seg = 1) = 0,14;
• P3 (выбор = a2 | seg = 1) = 0,1;
• P3 (выбор = A3 | SEG = 1) = 0,03.

Результат не выглядит таким впечатляющим, потому что окончательная вероятность покупки билета для самого удобного полета не так высока. Это специфичность розлива и захвата пассажирских потоков - условные вероятности и условные распределения вступают в игру.

Что происходит с теми, кто не может позволить себе купить такой билет? Если сумма средств пассажира попадает в интервал:

Он больше не сможет позволить себе полет в коде. В этом случае у него будет две альтернативы, доступные ему: выберите рейс с удобным или длинным соединением. На основании доступной утилиты, вероятности выбора следующие:

• P3 (выбор = a2 | seg = 2) = 0,77;
• P3 (выбор = A3 | SEG = 2) = 0,23.

u = np.array ([0,20, 0,06])

print (u / u.sum ())

[0,76923077 0,23076923]

Вероятность покупки билета в этом случае будет:

rvdem_3 = гамма (a = 10, loc = 230, scale = 12) print (rvdem_3.sf (325)- rvdem_3.sf (370)) 0,45418357596776533

Тогда полученные вероятности выбора для таких путешественников следующие:

• P3 (выбор = a2 | seg = 2) = 0,35;
• P3 (выбор = A3 | SEG = 2) = 0,1.

Путешественники, чья сумма денег находится в диапазоне [305 325), могут позволить себе только рейс A3. Вероятность покупки билета по цене 305 для этого сегмента составляет:

rvdem_3 = гамма (a = 10, loc = 230, scale = 12) print (rvdem_3.sf (305)- rvdem_3.sf (325)) 0,17088396696109864

В конечном счете, вероятности покупки билета для конкретного рейса будут выражены как простая сумма:

Пассажирский трафик H3

будет разделен между авиакомпаниями следующим образом:

• P3 (выбор = A1) = 0,14;
• P3 (выбор = A2) = 0,1+0,35 = 0,45;
• P3 (выбор = A3) = 0,03+0,1+0,17 = 0,3.

Вероятность p (buy = 0), что билет не будет куплен вообще 0,1, что в сумме с вышеупомянутыми вероятностями выбора дает 1. Это означает, что объем предоставляемого пассажирского потока полностью учитывается.

Сделав то же самое для пассажирского потока H2, мы получаем следующее:

• P2 (выбор = A2) = 0,1;
• P2 (выбор = A3) = 0,38.

Пассажирский трафик H1, хотя и не совместно используется между авиакомпаниями, но из -за цены 190 ue некоторая его доля будет пролита, поэтому мы все равно можем представить вероятность выбора полета P1 (выбор = A1), которая будет определена по цене (вероятность покупки билета по этой цене)::

rvdem_1 = гамма (a = 12, loc = 100, scale = 8) print (rvdem_1.sf (190))

0,5494501693973257

Было бы подробно описать все значения α, но, поскольку мы уже получили определенные значения фракций, мы напишем все в более короткой форме:

Для авиакомпании оптимизация соглашений о коде - это проблема упаковки с рюкзаком с двоичной переменной, равной одной или нулевым, когда выбран потенциальный полет для обмена или нет. Основные проблемы начинаются при оценке значения элементов, нанесенных в рюкзак. В простом случае авиакомпания может решить, что она зависит от бренда: если она привлекательна, то полет в коде также будет привлекательным. В этом наивном подходе ценность элемента, уложенного в рюкзаке, просто увеличивается пропорционально некоторому фактору.

Более развитым подходом является использование нескольких критериев привлекательности для выбора элемента. Каждый предмет - это маршрут, который имеет время вылета и прибытия, а также соединения, которые могут варьироваться как по продолжительности, так и по типу. Следовательно, выбор одного элемента меняет ценность всех остальных, как тех, которые уже в рюкзаке, так и еще не упакованы. Это означает, что все α должны рассчитывать каждый раз, когда выбирается элемент. Однако, умножая все H на соответствующие цены, вы можете получить вполне разумные оценки дохода, и, что наиболее важно, вы можете выяснить, с кем и на каких условиях заключите соглашение.

Метод довольно грубый, но следует отметить, что он связывает предпочтения путешественника с перераспределением пассажирского трафика. Delta Airlines, один из пионеров в оптимизации соглашений о CodeShare, сообщила, что эта оценка совместных маршрутов обеспечила дополнительные годовые доходы до 50 миллионов долларов. Это был не только один из самых выдающихся результатов за 2000 -е годы, но и прямое доказательство важности предпочтений путешественника. Позже Air Canada показала, что этот метод обеспечил до 80% больше еженедельных доходов, чем наивный метод, который только учитывает влияние бренда.

Этот метод плохой в том смысле, что он делит проблему на две части: сначала нам нужно ранжировать альтернативы и рассчитать оптимальные доли H, а затем помните, что все H являются случайными и рассчитывают оптимальные квоты отдельно. Разделение задач упрощает вычисление, но не приводит к оптимальному результату.

Моделирование и оптимизация

Авиакомпания A1 должна найти не только лучшие цены, но и квоты: W (1) 3 - количество мест, зарезервированных для совместного использования кодов, и W (1) 1 - это количество мест для тех, кто перемещается от A до B. Если мы обозначим v емкостью самолета, то простое условие для квот удовлетворено: w (1) 1+W (1) 3⩽V (1) - то же самое для номера. Q (1) 1+Q (2) 3+Q (3) 3⩽W (1) 1 и Q (1) 3⩽W (1) 3.

Обычно целевая функция без затрат и состоит только в увеличении доходов, полученного путем выбора совместного рейса. Однако в дополнение к выручке, существуют также расходы, которые оказывают значительное влияние на прибыльность рейсов. Чтобы оптимизировать прибыль, мы представляем следующие затраты:

• CFIX - Фиксированные затраты, например: оплата экипажа, сборы в аэропорту за парковку, взлету и посадку, авиационная безопасность.
• CVAR - переменные затраты, которые зависят от количества пассажиров, например: сборы за предоставление комплекса терминала аэропорта, обработка багажа. Это также будет включать в себя затраты на керосин, поскольку его количество также зависит от количества пассажиров и багажа, но для простоты мы передадим его в CFIX. ПУТА CVAR = CVARQ, например, CVAR может быть равным 25 C.U., значение которого просто умножается на количество пассажиров - Q.
• Цена (2) CH - затраты на места, приобретенные у операционного перевозчика для полета в коде.

Тогда средняя прибыль A1 будет следующей функцией:

Прибыль второй авиакомпании:

Можно подумать, что если A1 заключит соглашение с A2, то прибыль A3 не должна вызывать беспокойства. На самом деле, код имеет очень интересное последствие: конкурентное давление. Поэтому давайте записываем целевую функцию для A3:

Мы знаем, что hj~ -поуссон (λj). Зная, что PJ (Choice = AI), мы могли бы записать количество билетов, приобретенных Q (i) J как:

и дополнительно приближают биномиальное распределение с помощью нормального распределения. Даже для небольших значений HJ, это стандартная практика, но путешественники из H1 и H3 являются случайной смесью - нет такого понятия, как впервые продавать билеты только для тех, кто от H1, а затем продает оставшиеся места только для тех, от H3. Следует также отметить, что если аэропорты A и B разделены на значительное количество часовых поясов, смесь H2 и H3 будет иметь другой зависимый от времени композицию. Например, если A3 значительно снижает цену ночью, то пассажиры с H3 можно увидеть, потому что у них может быть дневное время, а не в ночное время.

Важно помнить, что данные всегда на первом месте. Даже если мы записали, HJ-Poisson (λj) является чрезвычайно грубым приближением, взятым только ради примера. Вместо распределения Пуассона всегда есть очень сложное условное распределение, которое происходит из данных.

Смешивание пассажирских потоков, ограниченной пропускной способности самолетов, квот и многих других нюансов делает невозможным получение распределения количества проданных билетов, продаваемых аналитически. Чтобы получить достаточные значения Q, необходимо моделировать процесс продаж.

Перед моделированием чего -либо необходимо определить основные параметры проблемы.

Предположим, что маршрут A → B → C является маршрутом Vladivostok-Moscow-Sochi: VVO → SVO → AER.

Пусть рейсы будут управлять следующими самолетами:

• VVO → SVO - управляется авиакомпанией A1 на самолетах A350 с емкостью V = 325.
• SVO → AER - управляется авиакомпанией A2 на самолетах A320 с емкостью V = 180.
• SVO → AER - эксплуатируется авиакомпанией A3 на самолетах Boeing 737 с емкостью V = 190.

Фиксированные затраты будут следующими:

• C (1) Исправление - 48360 C.U.;
• C (2) Исправление - 10270 C.U.;
• C (2) Исправление - 9890 C.U.

Переменные затраты:

• C (1) VAR - 6,8 C.U. / пассажир.
• C (2) VAR - 5,4 C.U. / пассажир.
• C (2) var - 5,1 C.U. / пассажир.

Предположим, что пассажирские потоки распределяются следующим образом:

• H12Poisson (λ1 = 370);
• H22Poisson (λ2 = 350);
• H32Poisson (λ3 = 110).

def prob_in_trafic (цены): цена_1, цена_2, цена_3 = цена rvdem_1 = гамма (a = 12, loc = 100, scale = 8) rvdem_2 = гамма (a = 8, loc = 60, scale = 7) rvdem_3 = гамма (a = 10, loc = 230, scale = 12) pb_11 = rvdem_1. = 1 - PB_11

ph \ _1 = \ [pb \ _10, pb \ _11 \]

UH \ _2 = np.Array (\ [0,14, 0,1 \]) pseg \ _2 = uh \ _2 / uh \ _2.sum ()

Если цена \ _2> цена \ _3: PBP \ _22 = RVDEM \ _2.SF (цена \ _2) PBP \ _23 = RVDEM \ _2.SF (цена \ _3) - RVDEM \ _2.SF (цена \ _2) PB \ _22 = PBP \ _22 \* PSEG \ \ PSEG. PB \ _23 = PBP \ _22 \* PSEG \ _2 \ [1 \] + PBP \ _23 ELS

PB \ _20 = 1 - PB \ _22 - PB \ _23

PH \ _2 = \ [PB \ _20, PB \ _22, PB \ _23 \]

UH \ _3 = np.Array (\ [0,2, 0,06 \]) PSEG \ _3 = UH \ _3 / UH \ _3.Sum ()

if (цена \ _1 + цена \ _2)> (цена \ _1 + цена \ _3): pbp \ _32 = rvdem \ _3.sf (цена \ _1 + цена \ _2) Pbp \ _33 = rvdem \ _3.sf (цена \ _1) цена \ _3) -rvdem \ _3.SF (цена \ _1) - rvdem \ _3. PB \ _32 = PBP \ _32 \* PSEG \ _3 \ [0 \] PB \ _33 = PBP \ _32 \* PSEG \ _3 \ [1 \] + PBP \ _33 ELSE: PBP \ _32 = RVDEM \ _3.SF (цена \ _1 + цена \ _2) PB rvdem \ _3.sf (цена \ _1 + цена \ _3) Pb \ _32 = PBP \ _32 PB \ _33 = 0

PB \ _30 = 1 - PB \ _32 - PB \ _33

ph \ _3 = \ [pb \ _30, pb \ _32, pb \ _33 \]

вернуть ph \ _1, ph \ _2, ph \ _3

def Sales (p): h_1 = poisson.rvs (mu = 370) h_2 = poisson.rvs (mu = 350) h_3 = poisson.rvs (mu = 110)

h \ _all = np.sum (\ [h \ _1, h \ _2, h \ _3 \]) p \ _in \ _h = np.array (\ [h \ _1, h \ _2, h \ _3 \]) / h \ _all

v \ _1, V \ _2, V \ _3 = 325, 180, 190 Q \ _1, Q \ _2, Q \ _3 = 0, 0, 0 для iter в диапазоне (H \ _all): Pass \ _in \ _h = np.random.choice (\ [1, 2, 3 \], p = p \ _in \ _h _hin \ _hin. 1: если np.random.choice (\ [0, 1 \], p = p \ [0 \]): если q \ _1 <v \ _1: q \ _1 += 1

Если пройти \\\ _ в \\\ _ h == 2: a \\\ _ i = np.random.choice (\\\ [0, 2, 3 \\\], p = p \\\ [1 \\\]) Если a \\\ _ i == 2: Если Q \\\ _ 2 <V \\\\ _ 2: Q \\\ _ 2 += 1 Если a \\\ _ i == 3: Если Q \\\ _ 3 <V \\\\ _ 3: Q \\\ _ 3 += 1

Если пройти \\\ _ в \\\ _ h == 3: a \\\ _ i = np.random.choice (\\\ [0, 2, 3 \\\], p = p \\\ [2 \\\]) Если a \\\ _ i == 2: Если Q \\\ _ 2 <V \\\\ _ 2: Q \\\ _ 2 += 1 Если Q \\\ _ 1 <V \\\\ _ 1: Q \\\ _ 1 += 1 Если a \\\ _ i == 3: Если Q \\\ _ 3 <V \\\\ _ 3: Q \\\ _ 3 += 1 Если Q \\\ _ 1 <V \\\\ _ 1: Q \\\ _ 1 += 1

Возврат Q \ _1, Q \ _2, Q \ _3

def Prefit_a (цены, Q): refit_1 = q [0] * цены [0] - q [0] * 6.8 - 48360 Profit_2 = Q [1] * Цены [1] - Q [1] * 5,4 - 10270 PROFIT_3 = Q [2] * Цены [2] - Q [2] * 5,1 - 9890 return Prefit

def e_profit (цены, n_iter): p = prob_in_trafic (цены) return np.mean ([prefit_a (цены, продажи (p)) для _ в диапазоне (n_iter)], ось = 0)

Теперь мы можем начать моделирование и оптимизацию. Возникают вопросы: что и как оптимизировать? Что и что сравнить, чтобы увидеть, есть ли увеличение прибыли?

В идеале каждая авиакомпания хочет увеличить свою прибыль, но изменения в цене билетов одной авиакомпании влияют на весь пассажирский трафик. Эти изменения замечены другими авиакомпаниями, и они также изменяют цену, что снова приводит к изменениям пассажирских потоков. Это означает, что прирост прибыли не может быть достигнут путем применения метода оптимизации только один раз. Таким образом, существует только одно требование для метода-он должен показать неотрицательное увеличение прибыли для всех параметров.

Предположим, что ни одна авиакомпания не заключила соглашения о кодешнике, и считают, что следующие цены оптимальны:

• Цена (1) 1 = 185;
• Цена (2) 2 = 114;
• Цена (3) 2 = 110.

Тогда распределение их прибыли будет следующим:

Цены = [185, 114, 110]

Q_DATA = [] refit_data = [] p = prob_in_trafic (цены)

Для I в диапазоне (1000): Q = Продажи (P) Q_DATA.Append (Q) PROFIT_DATA.Append (PROFIT_A (цены, Q))

Q_DATA = np.Array (Q_Data) PROFIT_DATA = np.Array (PROFIT_DATA) Рис.

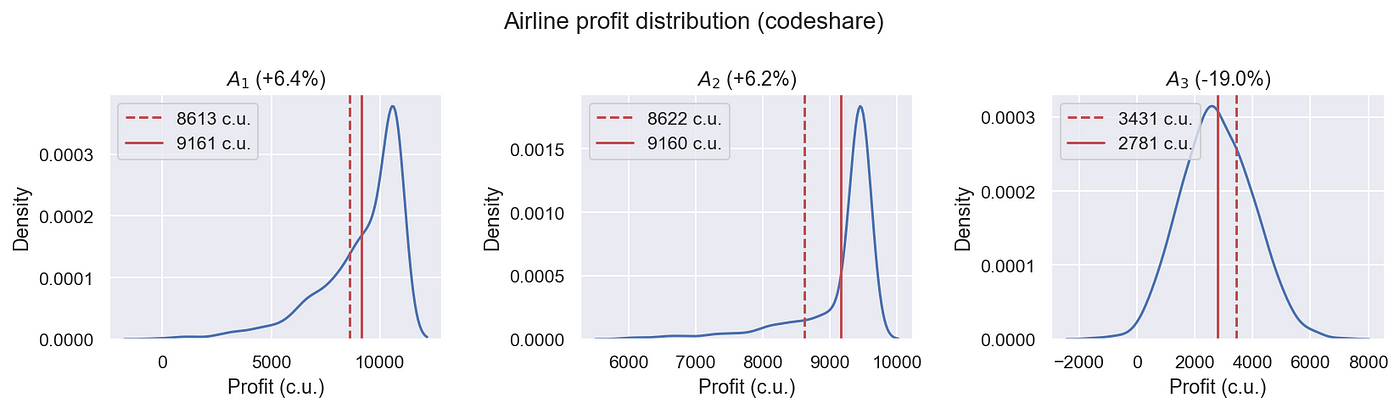
sns.kdeplot (reform_data [: 0], ax = ax [0]) e_pa_1 = np.mean (prefit_data [: 0]) ax [0] .axvline (e_pa_1, color = 'c3', label = f '{e_pa_1: .0f} c.') ax [0]. ax [0] .set_title (r '$ a_ {1} $') ax [0] .set_xlabel ('refit (c.u.)')

sns.kdeplot (reform_data [:, 1], ax = ax [1]) e_pa_2 = np.mean (prefit_data [:, 1]) ax [1] .axvline (e_pa_2, color = 'c3', label = f '{e_pa_2: .0f} c. ax [1] .set_title (r '$ a_ {2} $') ax [1] .set_xlabel ('refit (c.u.)')

sns.kdeplot (reform_data [:, 2], ax = ax [2]) e_pa_3 = np.mean (prefit_data [:, 2]) ax [2] .axvline (e_pa_3, color = 'c3', label = f '{e_pa_3: .0f} c. ax [2] .set_title (r '$ a_ {3} $') ax [2] .set_xlabel ('refit (c.u.)')

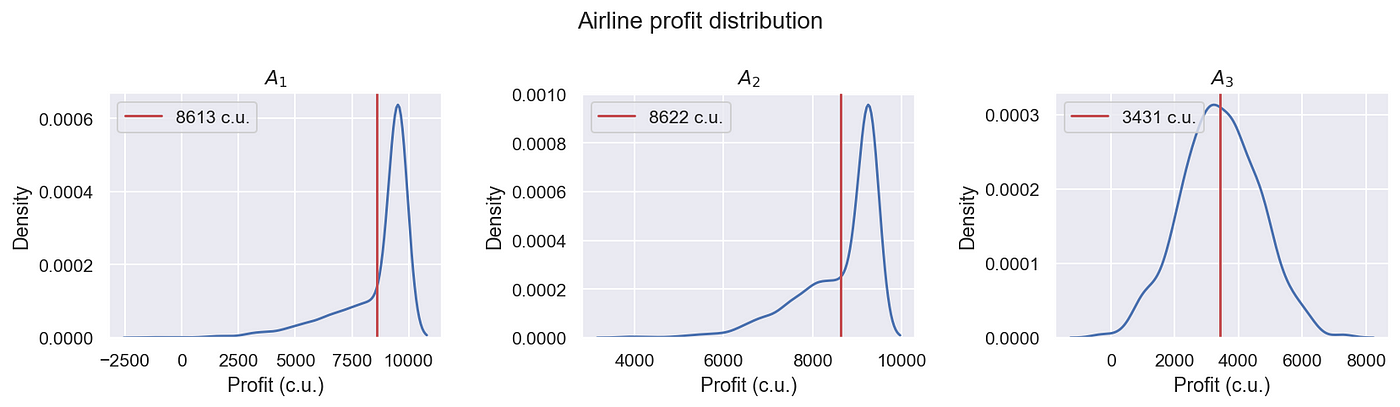
plt.suptitle ('распределение прибыли авиакомпании') plt.tight_layout ();

Для авиакомпании A3 цена явно не лучшая цена. Тем не менее, сейчас нас интересует, как именно будет изменяться средняя прибыль авиакомпаний A2 и A3, если они заключатся в соглашение об кодешнике друг с другом.

def prob_in_trafic_ch (цены): цена_1, цена_2, цена_3, цена_ч = цена [:-1] rvdem_1 = гамма (a = 12, loc = 100, шкала = 8) rvdem_2 = гамма (a = 8, loc = 60, шкала = 7) rvdem_3 = гамма (a = 10, loc = 230, scale = 7) rvdem_3 = гамма (а = 10, локация =

PB \ _11 = rvdem \ _1.sf (цена \ _1) Pb \ _10 = 1 - Pb \ _11

ph \ _1 = \ [pb \ _10, pb \ _11 \]

UH \ _2 = np.Array (\ [0,14, 0,1 \]) pseg \ _2 = uh \ _2 / uh \ _2.sum ()

Если цена \ _2> цена \ _3: PBP \ _22 = RVDEM \ _2.SF (цена \ _2) PBP \ _23 = RVDEM \ _2.SF (цена \ _3) - RVDEM \ _2.SF (цена \ _2) PB \ _22 = PBP \ _22 \* PSEG \ \ PSEG. PB \ _23 = PBP \ _22 \* PSEG \ _2 \ [1 \] + PBP \ _23 ELS

PB \ _20 = 1 - PB \ _22 - PB \ _23

PH \ _2 = \ [PB \ _20, PB \ _22, PB \ _23 \]

UH \ _3 \ _CH = np.Array (\ [0,28, 0,2, 0,06 \]) PSEG \ _3 \ _CH = UH \ _3 \ _CH / UH \ _3 \ _CH.SUM () UH \ _3 = np.Array (\ [0,2, 0.06 \]) PSEG \ _3 = uh \ _3 = uh \ _3 = uh \ _3 = uh \ uh \ _3.sum ()

Если цена \ _CH> (цена \ _1 + цена \ _2)> (цена \ _1 + цена \ _3): PBP \ _31 = RVDEM \ _3.SF (цена \ _CH) PBP \ _32 = RVDEM \ _3.SF (цена \ _1 + _2) -rvdem \ _3. PBP \ _33 = rvdem \ _3.SF (цена \ _1 + цена \ _3) - rvdem \ _3.sf (цена \ _1 + цена \ _2) Pb \ _31 = PBP \ _31 \* PSEG \ _3 \ _CH \ [0 \ \ _32 = PBP \ _31 \ _ PSEG \ _3 \ _CH \ [1 \] + PBP \ _32 \* PSEG \ _3 \ [0 \] PB \ _33 = PBP \ _31 \* PSEG \ _3 \ _CH \ [2 \] + PBP \ _32 \* PSEG \ _3 \ [1 \] + PBP \ _33333333: PB \ _333333333 PB \ _32 = 0 PB \ _33 = 0

PB \ _30 = 1 - PB \ _31 - PB \ _32 - PB \ _33

ph \ _3 = \ [pb \ _30, pb \ _31, pb \ _32, pb \ _33 \]

вернуть ph \ _1, ph \ _2, ph \ _3

def sales_ch (p, w_1): h_1 = poisson.rvs (mu = 370) h_2 = poisson.rvs (mu = 350) h_3 = poisson.rvs (mu = 110)

h \ _all = np.sum (\ [h \ _1, h \ _2, h \ _3 \]) p \ _in \ _h = np.array (\ [h \ _1, h \ _2, h \ _3 \]) / h \ _all

V \ _1, V \ _2, V \ _3 = 325, 180, 190 Q \ _1, Q \ _1 \ _CH, Q \ _2, Q \ _3 = 0, 0, 0, 0

Для iter в диапазоне (h \ _all): pass \ _in \ _h = np.random.choice (\ [1, 2, 3 \], p = p \ _in \ _h), если Pass \ _in \ _h == 1: if np.random.choice (\ [0, 1 \], p = p \ [0 \]): if q \ _1 <\ _1 <\ _1 <\ _1 <\ _1 <\ _1 <\ _1 <\ W \ _1: Q \ _1 += 1

Если пройти \\\ _ в \\\ _ h == 2: a \\\ _ i = np.random.choice (\\\ [0, 2, 3 \\\], p = p \\\ [1 \\\]) Если a \\\ _ i == 2: Если Q \\\ _ 2 <V \\\ _ 2 - W \\\ _ 1: Q \\\ _ 2 += 1 Если a \\\ _ i == 3: Если Q \\\ _ 3 <V \\\\ _ 3: Q \\\ _ 3 += 1

Если пройти \\\ _ в \\\ _ h == 3: a \\\ _ i = np.random.choice (\\\ [0, 1, 2, 3 \\\], p = p \\\ [2 \\\]) Если a \\\ _ i == 1: Если Q \\\ _ 1 \\\ _ CH <W \\\ _ 1: Q \\\ _ 1 \\\ _ CH += 1 Если a \\\ _ i == 2: Если Q \\\ _ 2 <V \\\ _ 2 - W \\\ _ 1: Q \\\ _ 2 += 1 Если Q \\\ _ 1 <V \\\ _ 1 - W \\\ _ 1: Q \\\ _ 1 += 1 Если a \\\ _ i == 3: Если Q \\\ _ 3 <V \\\\ _ 3: Q \\\ _ 3 += 1 Если Q \\\ _ 1 <V \\\ _ 1 - W \\\ _ 1: Q \\\ _ 1 += 1

Возврат Q \ _1, Q \ _1 \ _CH, Q \ _2, Q \ _3

DEF PROFIT_A_CH (цены, Q, W_1): PROFIT_1 = (Q [0] * Цены [0] + Q [1] * Цены [-2]) - (Q [0] + Q [1]) * 6,8 - W_1 * Цены [-1] - 48360 PROFIT_2 = (Q [2] * ЦЕНЫ [1] + W_1 * * ЦЕНЫ [-1]) - (Q [2] * 5.4. PROFIT_3 = Q [3] * Цены [2] - Q [3] * 5.1 - 9890 return Profit_1, Profit_2, Profit_3

def e_profit_ch (цены, w_1, n_iter): p = prob_in_trafic_ch (цены) return np.mean ([prefit_a_ch (цены, sales_ch (p, w_1), w_1) для _ в диапазоне (n_iter)], axis = 0)

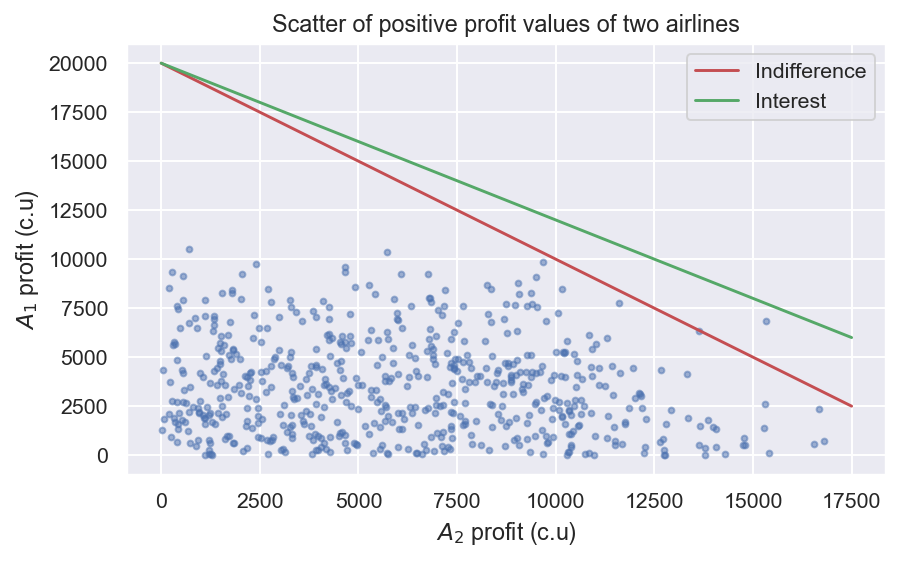
Давайте посмотрим на все значения прибыли A1 и A2, которые одновременно больше нуля:

PA_1 = [] pa_2 = [] pa_3 = [] pp = [] для i в диапазоне (10000): pra_1 = np.random.randint (150, 270) pra_2 = np.random.randint (111, 170) PRA_3 = 110 PRA_CH = np.random.randint (pra_1 + pra_2, 500). np.random.randint (pra_2, pra_1_ch) цены = pra_1, pra_2, pra_3, pra_1_ch, pay_ch w_1 = np.random.randint (0, 110) pa = e_profit_ch (цены, w_1, 1), если pa [0]> 0 и pa [1]> 0: pa_1. PA_2.Append (PA [1]) PA_3.Append (PA [2]) PP.Append ([Цены, W_1]) ​​PLT.PLOT (PA_2, PA_1, 'BO', MS = 3, ALPHA = 0,5)

x = np.linspace (0, 17500) y_1 = -x + 20000 y_2 = -0,8 * x + 20000

plt.plot (x, y_1, 'c3', label = 'безразличие') plt.plot (x, y_2, 'c2', label = 'inest')

plt.xlabel (r '$ a_ {2} $ profit (c.u)') plt.ylabel (r '$ a_ {1} $ profit (c.u)') plt.title ('разброс положительных значений прибыли двух авиакомпаний')

plt.legend ()

plt.show ()

Набор точек ограничен сверху некоторой выпуклой выпуклой и монотонно уменьшающейся функцией, которая содержит все точки комплекта сэффективного Парето. Если этот набор был симметричным, то точка набора, которая наиболее близка к линии, отключающему равные сегменты от оси координат в качестве оптимальной точки. Этот подход называется безразличным подходом. Эффективный набор почти никогда не симметричен, поэтому участники заинтересованы в том, чтобы убедиться, что асимметрия обязательно учитывается при принятии совместного решения. В этом случае точка, ближайшая к линии над набором и параллельна линии, проходящей через точки максимального процента, принимается в виде оптимальной точки (0, прибыль ∗ 1) и (прибыль ∗ 2,0).

Конструкция такого набора для проблемы в стохастической форме всегда требует исследования и приближения - его нельзя построить аналитически. Пусть точки максимального процента будут следующими: (0, 12000) и (17500, 0). В качестве линии, параллельной другой линии, проходящей через точки максимального интереса, давайте возьмем линию с уравнением y = -0,8x+20000. Тогда оптимальные цены будут принимать следующие значения:

• Цена (1) 1 = 185;
• Цена (2) 2 = 114;
• Цена (1) CH = 345;
• Цена (2) CH = 120;
• W (1) 3 = 29.

После введения полета Codeshare распределения прибыли будут выглядеть следующими:

цены_opt = [185, 114, 110, 345, 120] W_OPT = 29 P = prob_in_trafic_ch (цена_opt)

Q_CH_DATA = [] refit_ch_data = []

Для I в диапазоне (1000): q = sales_ch (p, w_opt) q_ch_data.append (q) prefit_ch_data.append (prefit_a_ch (цена_opt, q, w_opt))

Q_CH_DATA = np.array (Q_CH_DATA) PROFIT_CH_DATA = NP.Array (PROFIT_CH_DATA) PROCES_OPT = [185, 114, 110, 345, 120] W_OPT = 29 p = prob_in_trafic_ch (цена_опт)

Q_CH_DATA = [] refit_ch_data = []

Для I в диапазоне (1000): q = sales_ch (p, w_opt) q_ch_data.append (q) prefit_ch_data.append (prefit_a_ch (цена_opt, q, w_opt))

Q_CH_DATA = np.array (Q_CH_DATA) PROFIT_CH_DATA = NP.Array (PROFIT_CH_DATA)

В дополнение к увеличению прибыли, мы спокойно решили проблему переговоров. Все алгоритмы для оптимизации соглашений о коде оптимизируют доход только одной авиакомпании. В конце концов, две авиакомпании (потенциальные партнеры), использующие такой алгоритм, встретятся на переговорах с различными цифрами - это означает, что в конечном результате все будет зависеть от того, как они будут вести переговоры. Создание парето-эффективного набора не только оптимизирует прибыль обеих авиакомпаний, но также делает переговоры намного проще, открывая более прямой и более короткий путь к теории игр-полностью устраняя человеческий элемент.

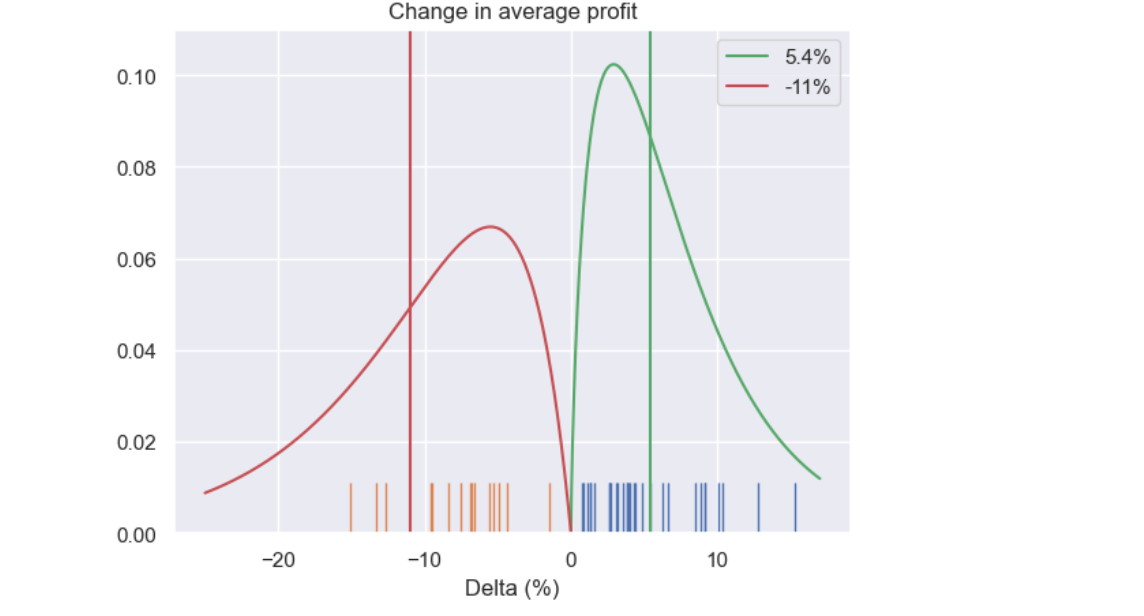
Идея розлива и захвата пассажиров очень глубока и имеет «далеко идущие» последствия. Сколько денег может быть заработано от такой идеи? Тестирование на реальных и моделируемых данных показывает, что с учетом предпочтений путешественников вместе с расчетом оптимальных квот и прибыли для обеих авиакомпаний дает значительные выгоды по сравнению с методами только предпочтения:

Красный цвет показывает, сколько утрачено авиакомпаниями, которые не заключались в соглашение - вы можете видеть, что в среднем потеря превышает прирост авиакомпаний, которые создали полет Codeshare.

Говорить о конкуренции как таковой, здесь не совсем уместно. Дело в том, что изменения пассажирских потоков влияют на всю сеть маршрутов. Негативные или положительные последствия таких изменений могут повлиять на всех участников сети: партнеров, конкурентов и даже тех, кто вообще не учитывался.

Авиакомпании также часто переоценивают привлекательность полетов Codeshare. Иногда цены завышены более чем на 100 долларов. Путешественники действительно очень ценят комфорт, но из -за чрезвычайно завышенной цены они выбирают менее удобные, но гораздо более дешевые варианты.

Тот факт, что проблема оптимизации является проблемой с двумя критериями, заслуживает особого внимания. Если операционный перевозчик (тот, кто на самом деле транспортирует пассажиров) не знает, как рассчитать парето-оптимальный набор решений, маркетинговый перевозчик (тот, кто продает билеты) может легко воспользоваться этим и заплатить меньше, чем следовало бы. И в конце концов, все, что ему нужно сделать, это просто отслеживать продажи потенциального филиала.

Кстати, в этой статье рассматривались только один наиболее распространенный тип кода свободного продажи-когда обе авиакомпании могут публиковать полет другого перевозчика как свой собственный с небольшими или без ограничений на количество мест, которые могут быть проданы (в пределах пропускной способности самолета или установленных ограничений). Тем не менее, рассматриваемый метод оптимизации также подходит для других типов кодекса, например, блочного пространства-когда количество маркетинговых перевозчиков, которое продается маркетинговым перевозчиком. Метод также подходит для оптимизации интернет -соглашений, когда одна авиакомпания просто распознает документы перевозки другой авиакомпании. Interline также влияет на привлекательность, но требует меньше ограничений со стороны авиакомпании.

С одной стороны, с учетом различных соглашений делает задачу немного более сложной, но с другой стороны, она позволяет авиакомпании объединять различные условия, оптимизируя не только прибыль, но и привлекательность как для обычных, так и для новых пассажиров из -за обширной сети маршрутов.

В заключение

Увеличение прибыли на 5% только из -за соглашений о коде не является плохим результатом. Это может быть больше? Конечно, да. Эту проблему можно рассматривать как расширение проблемы назначения флота IFAM на основе моделирования композиции пассажира и принципа узкого места/захвата пассажира. Полет Codeshare может быть концептуализирован как полете, управляемый некоторыми виртуальными самолетами. Это означает, что можно использовать уже устоявшиеся методы для дальнейшей оптимизации-например, оптимизация на уровне динамического ценообразования (подклассов), а не усредненных и грубых значений. В этом случае прирост прибыли может быть еще больше.

IFAM рассматривает только одну авиакомпанию, но инновационность этой модели именно в том, что впервые начал учитывать влияние изменений на некоторые пассажирские потоки на изменения в других пассажирских потоках. Стало возможным «пролить» в одном месте и «собрать разлив» в другом. В ifam нет полетов CODESHARE, нет аттракциона, и пассажирские потоки влияют только цена.

Сложность с расширением IFAM состоит в том, что каждый потенциальный общий рейс действительно должен рассматриваться как отдельный виртуальный самолет. В парке авиакомпании может быть более 100 или даже 1000 таких потенциальных самолетов. И это еще не все - решению IFAM обычно предшествует задача формирования графика, которая в значительной степени разработана с учетом апелляции путешественника. При добавлении рейсов CODESHARE, степень, в которой фиксированные графики полета виртуальных самолетов соответствуют фиксированным графикам, в которых необходимо учитывать реальные самолеты авиакомпании. Самое главное, что после выбора каждого виртуального самолета и цены билета необходимо будет рассчитать перераспределение пассажирских потоков по всей сети маршрутов.

Как было упомянуто в начале статьи, решение проблемы возможно только в том случае, если есть данные - точнее, огромное количество данных. Так или иначе, все сводится к моделированию дискретных вариантов, которые делают путешественники. Некоторые авиакомпании с большими историческими данными делают довольно хорошую работу с этим, но даже они не могут конкурировать с GDS (глобальная система распределения). Это связано с тем, что авиакомпании имеют данные о пассажирских потоках только своих маршрутных сетей, в то время как GDS видит всю картину и способна анализировать гораздо большее количество как маршрутов, так и сценариев изменений в пассажирских потоках. Тем не менее, следует сказать, что это относится только к новому поколению GDS. К сожалению, более старые системы никогда не занимались такими задачами и не справлялись с ними условно.

В действительности ни одна авиакомпания никогда не сможет своевременно оценивать перераспределение пассажирских потоков, просто потому, что ей требуются данные других авиакомпаний. В этой статье мы затронули, хотя и мимоходом, по теме многокритериальной оптимизации, которая облегчает переговоры, что, в свою очередь, приводит нас к теории игры. Но эта теория неоднократно доказала, что кооперативные стратегии являются наиболее прибыльными и устойчивыми. Чтобы достичь этого, необходимо новое поколение GDS, тогда любая авиакомпания будет иметь доступ к анонимным данным о пассажирском движении других авиакомпаний. Благодаря этому можно достичь качественно нового уровня оптимизации не только соглашений о коде, но и ряда других задач: графики, развертывание флота и т. Д.

Чтобы понять возможности GDS, давайте задаем простой вопрос: что произойдет, если в рассмотренной проблеме все рейсы выполнялись не тремя, а одной авиакомпанией? В этом случае только средняя сумма прибыли от всех рейсов может быть оптимизирована. Вы получаете обычную проблему IFAM, и прибыль в общей прибыли становится намного больше, чем от введения рейсов Codeshare. Единственная проблема заключается в том, что рейсы управляются различными авиакомпаниями. Централизованное руководство имеет гораздо больше преимуществ, но у него также есть трудности. Из -за недостаточных данных авиакомпании не могут этого сделать, но GDS может.