Как правила печати и тип звукости работают на основных и веселых языках программирования
8 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
4.2 Правила печати для Core
Полные правила печати дляОсновнойприведены на рисунке 2, но мы представим их шаг за шагом. Теперь у нас есть производители, потребители и заявления в качестве различных синтаксических категорий. Для каждой из этих категорий мы используем отдельную форму суждения:

Все судебные решения также неявно индексируются программой 𝑃, содержащей определения верхнего уровня. Однако, поскольку эти определения необходимы только при типике их вызовов (вызов правил), мы обычно опускаем индекс из презентации.



4.2.1 Типы данных и кода.Рисунок 2 содержит правила печати как для пары, так и для списка; Поскольку их правила настолько похожи, мы только явно обсуждаем правила пары:
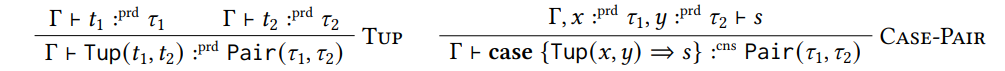
В правиле мы набираем конструктор пары, применяемый к двум аргументам в качестве производителя, а в паре правила мы набираем случай, который сопоставлен с шаблонами на этом конструкторе и привносит две переменные в область в качестве потребителя.
Правила набора типов для типов кодат выглядят точно так же, только роли производителей и потребителей поменяются.
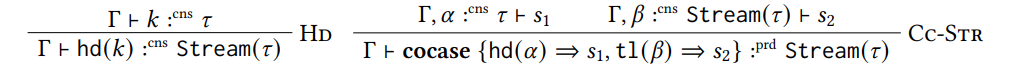
Большинство других правил напрямую соответствуют аналогичному правилу для развлечения. Например, при печати арифметических выражений мы должны только убедиться, что у всех подследований есть тип int.
Мы программы Typecheck используют два правила WF-Empty и WF-Cons. Первый используется для TypeCheck пустую программу, а правило WF-Cons расширяет программу TypeChecked с новым определением верхнего уровня. Когда мы печатаем тело этого определения верхнего уровня, которое мы собираемся добавить, мы расширяем программу с помощью этого определения, чтобы она могла обращаться к себе рекурсивно.
4.3 Тип. Звукость
В этом разделе мы обсудим обоснованность типовых систем как для веселья, так и для ядра и показываем, что перевод [ -] сохраняет типичность терминов. Мы следуем за Райтом и Феллеизеном [1994], представляя типовую обоснованность как комбинацию прогресса и теоремы сохранения. Теорема 4.1 (прогресс, веселье).
Теорема 4.1 (прогресс, веселье).Позвольте 𝑡 быть закрытым термином в веселом, так что ⊢ 𝑡: 𝜏 для какого -то типа 𝜏. Тогда либо 𝑡 - это значение, либо есть какой -то термин 𝑡 ′, такой что 𝑡 ⊲ ′.
Это может быть легко доказано с помощью индукции при вводе дериваций. Из -за наличия конструкции метки/goto стандартная формулировка теоремы (сильного) сохранения не сразу же содержится для развлечения (также см. Обсуждение в Приложении C). Следующая слабая форма сохранения снова может быть легко доказана при индукции.
Теорема 4.2 ((слабая) сохранение, веселье).Пусть 𝑡, 𝑡 ′ быть в веселом уровне, так что 𝑡 ⊲ ′, γ окружающая среда и 𝑃 программа, такая, что γ ⊢𝑃 𝑡: 𝜏. Тогда есть тип 𝜏 ′, такой, что γ ⊢𝑃 ′ ′: 𝜏 ′.
Обычная сильная теорема сохранения требует 𝜏 ′ = 𝜏. Но на самом деле, небольшая вариация этой сильной формы может быть доказана для развлечения, адаптируя технику, найдшую в разделе 6 в [Wright and Felleisen 1994]. Таким образом, надежность сильного типа все еще держится.
Прежде чем мы сможем изложить аналогичные теоремы для Core, нам понадобится дополнительное определение в качестве условия завершения для оценки.
Определение 4.3 (утверждение терминала). Если 𝔭 - это значение производителя в ядре и ⋆ ковейскую, которая не выглядит свободной в 𝔭, то ⟨𝔭 | ⋆⟩ называется терминальным утверждением.
Терминальные утверждения в ядре играют ту же роль, что и значения в веселье. Некоторые языки, основанные на последовательности, используют специальное заявление, сделанное вместо терминальных операторов для этой цели.
Теорема 4.4 (Прогресс, ядро).Пусть 𝑠 будет сфокусированным утверждением в ядре, такое, что ⊢ 𝑠. Тогда либо 𝑠 является утверждением терминала, либо есть некоторые ′ ′, такие что 𝑠 ⊲ ′ ′.
Для этой теоремы мы требуем, чтобы 𝑠 Было сосредоточено, в отличие от развлечения, где прогресс удерживается для любого (хорошо (хорошопленного) термина. Это потому, что мы использовали статическую фокусировку для полной оценки в ядре. Если бы вместо этого мы использовали динамическую фокусировку, это требование может быть отброшено, что соответствует использованию контекстов оценки (динамического) в веселом, вместо перевода в нормальную форму (статическую).
Теорема сохранения для ядра аналогична веселья.
Теорема 4.5 (сохранение, ядро).Пусть 𝑠, 𝑠 ′ быть утверждениями в ядре с 𝑠 ⊲ ′, γ окружающей средой и программой. Если γ ⊢𝑃 𝑠, то γ ⊢𝑃 ′ ′.

Наконец, мы приходим к важной собственности перевода между этими языками:

Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал
