Как стилизованные факты формируют будущее моделирования финансового рынка
28 июля 2025 г.Таблица ссылок
Аннотация, подтверждения, а также заявления и декларации
Введение
Фон и связанная работа
2.1 Моделирование финансового рынка на основе агента
2.2 Эпизоды флэш -аварии
Структура модели и настройка модели 3.1
3.2 Общее поведение трейдеров
3.3 Фундаментальный трейдер (Ft)
3.4 Momentum Trader (MT)
3,5 шумового трейдера (NT)
3.6 Market Maker (MM)
3.7 Динамика моделирования
Калибровка и проверка модели и целевая калибровка 4.1: данные и стилизованные факты для реалистичного моделирования
4.2 Калибровочный рабочий процесс и результаты
4.3 Проверка модели
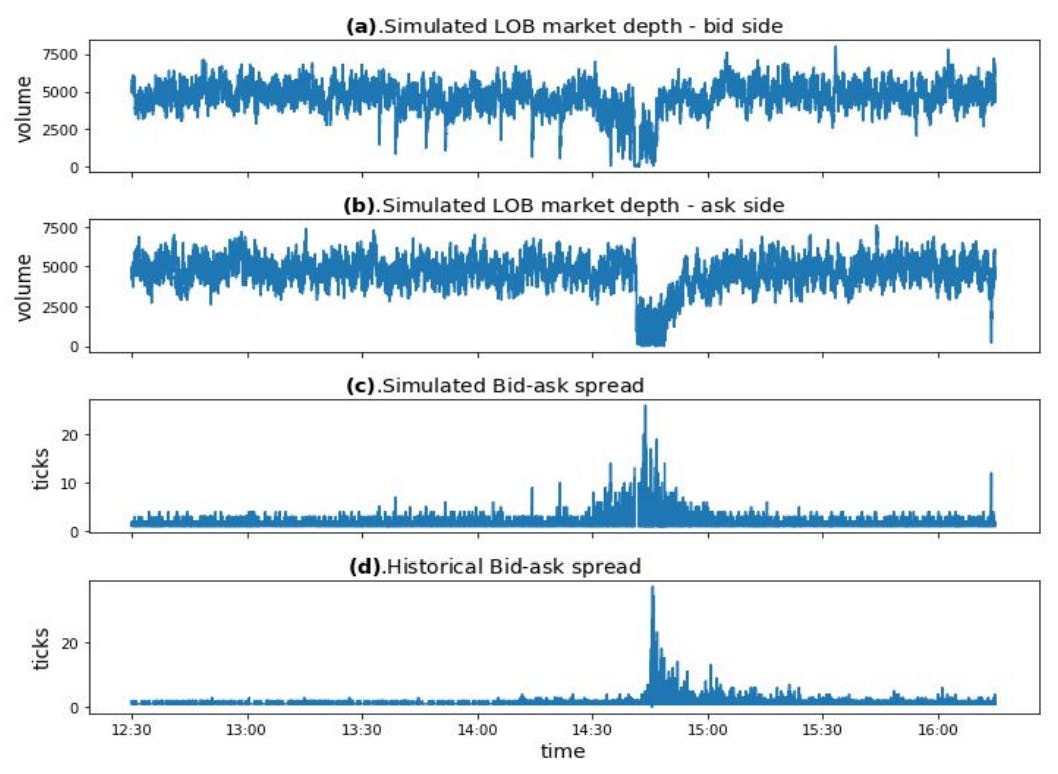
Сценарии флэш -аварии 2010 года и 5,1 моделирования исторической флэш -аварии
5.2 Флэш -авария в разных условиях
Мини -флэш -сценарии аварии и 6.1 Внедрение трейдера Spiking (ST)
6.2 Анализ мини -флэш -аварии
6.3 Условия для сценариев аварии мини -флэш -авара
Заключение и будущая работа
7.1 Сводка достижений
7.2 Будущие работы
Ссылки и приложения
4 калибровка и проверка модели
В этом разделе мы представляем методологию калибровки финансового рынка на основе агента. Калибровка означает поиск оптимального набора параметров модели, чтобы модель генерировала наиболее реалистичный моделируемый финансовый рынок. Во -первых, мы описываем реальные данные и связанные стилизованные факты на финансовых рынках. Затем мы определяем расстояние между историческими и смоделированными стилизованными фактами, которые действуют как функция потерь в процессе калибровки. Представлен рабочий процесс калибровки параметров, за которым следует подробная проверка предлагаемого высокочастотного симулятора финансового рынка.
4.1 Цель калибровки: данные и стилизованные факты для реалистичного моделирования
В процессе калибровки модели реальные данные о финансовом рынке необходимы для настройки цели калибровки. Мы собрали данные о высокочастотном ограниченном порядке по заказу фьючерсов E & P 500 с 3 мая 2010 года по 6 мая 2010 года [7]. Мы выбираем наиболее жидкий контракт в качестве целевого калибровки, который является договором, истекает в июне 2010 года. Наш набор данных включает в себя высокочастотную информацию для 10 уровней обновления книги «Ограничение заказа», как сторону покупки, так и на стороне продажи.
Данные временных рядов финансовой цены отображают некоторые интересные статистические характеристики, которые обычно называют стилизованными фактами. Согласно Sewell (2011), стилизованные факты относятся к эмпирическим выводам, которые настолько последовательны (например, в широком спектре финансовых инструментов и различных периодах времени), что они принимаются как истина. Стилизованный факт - это упрощенное представление эмпирического вывода на финансовых рынках. Успешное и реалистичное моделирование финансового рынка способна воспроизводить различные стилизованные факты. Эти стилизованные факты включают в себя распределение доходов, автокорреляцию доходности и кластеризацию волатильности. Функция потерь, используемая в процессе калибровки, построена путем измерения расстояния между историческими и смоделированными стилизованными фактами.
4.1.1.
Было обнаружено, что распределение доходности цен на все временные рамки. Другими словами, доходные распределения демонстрируют положительный избыток куртоза. Понимание положительного распределения доходности куртотических доходов важно для управления рисками, так как крупные цены на гораздо чаще встречаются, чем в обычно предполагаемых нормальных распределениях.
Следуя конвенции в литературе, в этой статье мы исследуем стилизованный факт доходности с жирным хвостом, изучив внутридневную доходность цены второго уровня. Исторические и смоделированные временные ряды на уровне миллисекунды, так и моделируемые серию средней цыскую цену в частоту второго уровня, и мы исследуем возврат средней ценности за каждую секунду. В частности, последняя цена снимок сделан в качестве цены за эту конкретную секунду. Доходность цены второго уровня рассчитывается соответственно. Наши эксперименты показывают, что разные временные масштабы не оказывают существенного влияния на конечные результаты. Основной метрикой, используемой для оценки характеристики жирого хвоста, является оценка холма индекса хвоста (Hill 2010). Более низкое значение оценщика холма подразумевает, что доходное распределение имеет более толстый хвост.
4.1.2 Автокорреляция возвратов
Автокорреляция определяется как математическое представление степени сходства между временным рядом и отставной версией того же временного ряда. Он измеряет взаимосвязь между прошлыми значениями переменной и ее текущим значением. Возьмите, например, автокорреляцию первого порядка. Положительная автокорреляция доходности первого порядка указывает на то, что положительный (отрицательный) возврат за один период склонна к положительному (отрицательному) возврату в последующем периоде. Вместо этого, если автокорреляция доходности первого порядка отрицательна, положительная (отрицательная) доходность обычно сопровождается отрицательной (положительной) доходностью в следующем периоде. Наблюдается, что в ряду доходов не хватает значительной автокорреляции, за исключением слабой отрицательной автокорреляции на очень короткие сроки. McGroarty et al. (2019) показывают, что негативная автокорреляция доходности значительно сильнее за меньший горизонт и исчезает в течение более длительного времени. Исследование наших данных также показывает этот стилизованный факт. На рисунке 1 показана функция автокорреляции во времени возврата второго уровня для фьючерсов на электронную службу S & P 500 за два дня. Мы видим, что автокорреляция значительно отрицательно от очень маленьких лагов, и отрицательная автокорреляция постепенно исчезает для больших лагов.

4.1.3 Кластеризация волатильности
Доходы от финансовой цены часто демонстрируют собственность кластеризации волатильности: большие изменения в ценах, как правило, сопровождаются большими изменениями, в то время как небольшие изменения в ценах, как правило, сопровождаются небольшими изменениями. Это свойство приводит к устойчивости амплитуд изменений цен (продолжение 2007). Установлено, что свойство кластеризации волатильности существует на временных масштабах, варьирующихся от минут до дней и недель. Кластеризация волатильности также относится к длинной памяти о доходности квадратной цены (McGroarty et al. 2019). Следовательно, кластеризация волатильности может проявляться медленной затухающей схемой при автокорреляции квадратных доходов. В частности, для коротких лагов функция автокорреляции в квадрате доходности является значительно положительной, а автокорреляция медленно распадается при увеличении лагов. На рисунке 2 показаны паттерны автокорреляции для квадратных возвратов второго уровня для фьючерсов на электронную службу S & P 500 за два дня. Показано, что стилизованный факт кластеризации волатильности явно существует в нашем собранном наборе данных о фьючерсах E & P 500.

4.1.4 Стилизованные факты расстояние как функция потерь
Целью для калибровки модели на основе агента является поиск оптимального набора параметров модели, чтобы модель генерировала реалистичный моделируемый финансовый рынок. Чтобы решить эту проблему оптимизации, важно иметь метрику, способную количественно оценить «реализм» имитационного финансового рынка. Прежде всего, реалистичный моделируемый финансовый рынок должен демонстрировать аналогичные характеристики на реальных финансовых рынках, таких как жирохводимый распределение доходности и уровень волатильности. Кроме того, реалистичные моделируемые финансовые данные также необходимы для воспроизведения других стилизованных фактов, таких как модели автокорреляции в отдачи и квадратных возвратах. Здесь мы разрабатываем стилизованное расстояние фактов, чтобы количественно оценить сходство между моделируемыми и историческими финансовыми данными. Четыре метрика рассматриваются в стилизованном расстоянии фактов: оценка холма индекса хвоста для абсолютных распределений возврата, волатильности, автокорреляции доходности и автокорреляции квадратных доходов. Для каждой метрики рассчитываются дифференциальная величина между смоделированным значением и историческим значением. Стилизованное расстояние фактов рассчитывается как взвешенная сумма четырех дифференциальных величин:

Подробные расчеты четырех величин в стилизованном расстоянии фактов представлены ниже.
Оценка холма известна тем, что выводит силовое поведение в хвостах экспериментальных функций распределения. После Franke and Westerhoff (2012) мы используем оценку холма индекса хвоста, чтобы оценить степень жирого хвоста при распределении абсолютной прибыли по средней цене. Обратите внимание, что абсолютное распределение возврата учитывается, поскольку нет необходимости различать экстремальную положительную и отрицательную доходность. В наших экспериментах рассчитывается оценка холма для моделируемой абсолютной доходности и исторической абсолютной прибыли соответственно. Абсолютная разница между двумя оценщиками холма представляет собой первую часть стилизованного расстояния фактов:

Вторая часть стилизованного расстояния фактов - это абсолютная разница в волатильности между моделируемыми доходами и историческими доходами:

Третья часть стилизованного расстояния фактов - это разница между моделируемыми и историческими автокорреляциями доходности. Эта часть в стилизованном расстоянии измеряет способность модели воспроизводить модели автокорреляции, обычно встречающиеся в исторических отдачи. Показано, что во времени возврата финансовой цены не хватает значительной автокорреляции, за исключением коротких временных масштабов, где существуют значительно отрицательные автокорреляции. Это явление поддерживается нашими эмпирическими данными. Для очень маленьких лагов автокорреляции являются отрицательными, в то время как для больших лагов автокорреляции становятся незначительными. Чтобы измерить расстояние в схемах автокорреляции между моделируемыми данными и историческими данными, мы вызываем функцию автокорреляции доходности и рассчитываем среднюю абсолютную разницу между автокорреляциями моделируемых временных рядов возврата и историческим временным рядом возврата для различных лагов:

Последняя часть стилизованного расстояния фактов - это разница между моделируемыми и историческими автокорреляциями квадратных доходов. Репликация моделей автокорреляции в квадратных возвратах указывает на способность модели воспроизводить стилизованный факт кластеризации волатильности. Эмпирически показано, что большие цены, как правило, сопровождаются другими большими изменениями цен, известными как явление кластеризации волатильности. Следовательно, хотя, как правило, нет существенных моделей автокорреляций доходности, автокорреляция квадратных доходов значительно положительно, особенно для небольших временных лагов. Кроме того, с учетом увеличения времени, автокорреляция квадратных возвратов отображает медленно распахнутую паттерн, как показано на рисунке 2. Аналогично разнице между автокорреляциями доходности ∆ACF 1, разница между автокорреляциями доходных доходности рассчитывается следующим образом.

Вышеуказанные четыре части, наряду с соответствующими весами, составляют стилизованное расстояние фактов в уравнении (3). Следующий вопрос - как определить связанный вес для каждой части стилизованного расстояния фактов. Основная руководящая идея заключается в том, что чем выше изменчивость выборки данной части в исторических данных, тем больше разница между смоделированным значением и историческим значением, которая все еще может быть признана незначительной. Естественный кандидат на каждый вес - это обратный дисперсию отбора проб для соответствующей части в стилизованном расстоянии фактов:

Обратите внимание, что стилизованное расстояние фактов является функцией параметров модели. Другими словами, учитывая набор параметров модели, существует уникальное стилизованное расстояние фактов, рассчитанное по моделируемым временным ряду, что соответствует этому конкретному набору параметров модели. Пусть θ обозначает вектор параметров модели, который должен быть оценен, уравнение (3) может быть переписано как:

Авторы:
(1) Кан Гао, Департамент компьютеров, Императорский колледж Лондон, Лондон SW7 2AZ, UK и Simudyne Limited, Лондон EC3V 9DS, Великобритания (kang.gao18@imperial.ac.uk);
(2) Perukrishnen Vytelingum, Simudyne Limited, London EC3V 9DS, Великобритания;
(3) Стивен Уэстон, Департамент компьютеров, Имперский колледж Лондон, Лондон SW7 2AZ, Великобритания;
(4) Уэйн Лук, Департамент компьютеров, Имперский колледж Лондон, Лондон SW7 2AZ, Великобритания;
(5) CE Guo, Департамент компьютеров, Имперский колледж Лондон, Лондон SW7 2AZ, Великобритания.
Эта статья естьДоступно на ArxivПод CC BY-NC-ND 4.0 Лицензия.
[7] Вечерние торговые сессии исключены. То есть промежуток данных с 8:00 утра до 5:00 дня на каждый день.
Оригинал
