Как привязки повысить четкость кода в функциональном программировании
7 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
2.2 Пусть привязки
Заветные связки важны, поскольку мы можем использовать их для устранения дублирования и сделать код более читабельным. В этом разделе мы вводим let-bindings для развлечения по дополнительной причине: они позволяют нам представить вторую конструкцию, которая дает 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus его название: 𝜇 𝜇-abstractions.

Веселые развязки являются стандартными и оцениваются путем замены значения 𝔱 на переменную 𝑥 в теле, который является термином. Аналог let-связывания в веселье-это 𝜇 𝜇-связывающее в ядре, которое также связывает переменную, с разницей в том, что тело 𝜇-связывания является утверждением. Легко можно увидеть, что 𝜇 𝜇-связки-это точный двойник 𝜇-связей, которые мы уже представили.
С помощью 𝜇- и 𝜇 𝜇-связки мы должны столкнуться с потенциальной проблемой, а именно утверждения формы ⟨𝜇𝛼.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩. Такое утверждение называется критической парой, так как оно потенциально может быть уменьшено как к 𝑠1 [𝜇𝑥.𝑠 ˜ 2/𝛼], так и 𝑠2 [𝜇𝛼.𝑠1/𝑥], которые могут быть источником неконфликта. Более тщательное осмотр правил показывает, что мы избегаем этой ловушки и всегда оцениваем утверждение до 𝑠1 [𝜇𝑥.𝑠 ˜ 2/𝛼]. Мы не допускаем уменьшения оператора до 𝑠2 [𝜇𝛼.𝑠1/𝑥], поскольку только значения 𝔭 могут быть заменены на переменные, а 𝜇𝛼.𝑠1 не является значением. Это ограничение точно отражает ограничение на оценку развязки LET в веселье. Другими словами, мы используем порядок оценки вызовов. Мы рассмотрим критическую пару и то, как она снова относится к различным порядкам оценки в разделе 5.6.

Мы можем заметить, что арифметическое выражение 2 ∗ 2 оценивалось только один раз, что именно то, что мы ожидаем от вызова.
2.3 Определения верхнего уровня
Мы вводим рекурсивные определения верхнего уровня для веселья и основного по двум причинам. Они позволяют нам писать более интересные примеры, и они иллюстрируют разницу в том, как обрабатываются рекурсивные вызовы. Расширение указано в определении 2.4.

Определения верхнего уровня не следует путать с первоклассными функциями, которые будут представлены позже, поскольку они не могут быть переданы в качестве аргумента или возвращены в результате. Они являются частью программы, которая состоит из списка таких определений высшего уровня. Определения верхнего уровня в веселом с любопытством также принимают ковариации как аргументы, даже если язык не содержит потребителей; Вы можете игнорировать это на данный момент. Если вы помните пример из введения, то вы можете вспомнить, что мы используем их для прохождения метки, но мы формально представим эту конструкцию в разделе 2.6.
Мы оцениваем призыв определения верхнего уровня, просматривая тело в программе и заменяя аргументы вызова для параметров в теле определения. Тело определения верхнего уровня-это термин в веселье и заявление в ядре. Эта разница объясняет, почему мы должны добавить дополнительный параметр 𝛼 в каждое определение верхнего уровня, когда мы переводим его; Этот параметр 𝛼 также соответствует дополнительному аргументу продолжения, когда мы обычно переводим функцию в стиль продолжения. Мы также могли бы указать, что корпус определения верхнего уровня в ядре должен быть производителем. Мы не делаем этого, потому что, когда мы в конечном итоге переводим ядро в машинный код, мы хотим, чтобы каждое определение верхнего уровня стало целью прыжка с аргументами без создания стека вызовов функции. В следующем примере показано, как это работает:
Пример 2.3Полем Используя определение верхнего уровня, мы можем представлять факторную функцию в Core.
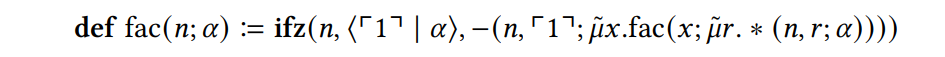
Для аргумента ⌜1⌝ это оценивается следующим образом:

В точке (∗) оценки мы теперь можем увидеть, как оценивается рекурсивный вызов. В веселье этот рекурсивный вызов будет иметь FAC FAC 1 ∗ (0) и потребовать функционального стека, но в ядре мы можем подняться на определение FAC с потребителем 𝜇𝑟. ˜ ∗ (⌜1⌝, 𝑟; ⋆) как дополнительный аргумент, который содержит информацию, что результат рекурсивного вызова должен быть связан с переменной 𝑟, а затем умножена на ⌜1⌝. Обратите внимание, что этот аргумент потребителя соответствует продолжению в стиле продолжения (в этом смысле, он может рассматриваться как урегулированный стек), и поэтому для ее реализации могут применяться основные методы, используемые в промежуточных представлениях и компиляторах на основе CPS.
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Ведущее изображение этого ведущего на Pexels.
Оригинал
