Однородность и нормальность: как проверить ваши экспериментальные данные
20 августа 2025 г.Таблица ссылок
Аннотация и 1. Введение
2. Определение эксперимента
3. Эксперимент дизайн и поведение
3.1 Latin Square Designs
3.2 Субъекты, задачи и объекты
3.3 поведение
3.4 меры
4. Анализ данных
4.1 Модельные предположения
4.2 Анализ дисперсии (ANOVA)
4.3 Сравнение лечения
4.4 Размер эффекта и анализ мощности
5. Ограничения эксперимента и 5.1 угрозы для заключения достоверности
5.2 Угрозы для внутренней достоверности
5.3 Угрозы для построения достоверности
5.4 Угрозы для внешней достоверности
6. Обсуждение и 6.1 продолжительность
6.2 Усилия
7. Выводы и дальнейшая работа, а также ссылки
4.1 Модельные предположения
Прежде чем мы начнем делать какие -либо выводы, мы должны оценить следующие допущения модели:
Все наблюдения независимы (независимость)
Разница одинакова для всех наблюдений (однородность)
Наблюдения в каждой группе лечения имеют нормальное распределение (нормальность)
Первое предположение учитывается принципом рандомизации, используемом в этом экспериментальном дизайне; Все меры одной выборки не связаны с показателями другой выборки. Второе и третье допущения оцениваются с использованием расчетных остатков [6, 16]. Чтобы оценить однородность дисперсий, мы используем график, чтобы показать график рассеяния стандартизированных остатков по сравнению с оценочными средними значениями (иногда называемыми подходящими значениями). Мы также используем тест Levene для однородности дисперсий [17]. Третье предположение (нормальность) оценивается с использованием нормального графика вероятности и применения теста Колмогоровсмирнова для нормальности [15, 26].
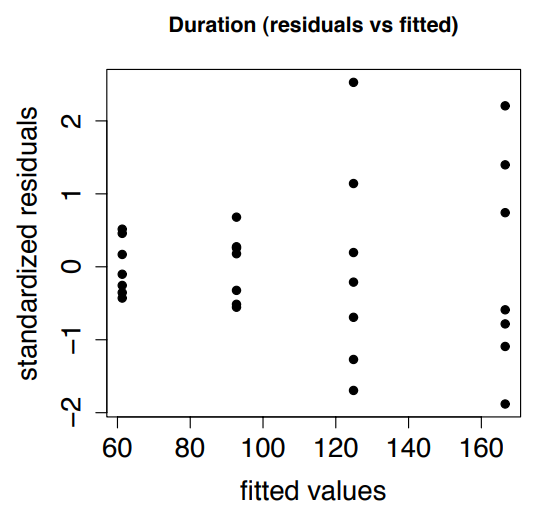
Выбор показателя продолжительности, на рис. 1 показан график рассеяния стандартизированных остатков в сравнении с установленными значениями. Нарушения предположения о дисперсии однородности могут быть обнаружены с помощью любого графика, отметив, что изменение в вертикальном направлении, по -видимому, различается в разных точках вдоль горизонтальной оси. В этом случае на рис. 1 показана другая картина между вертикальными точками. Применяя тест Левен [17], мы получаем значение p 0,0594. Установка альфа-уровня 0,05 этот тест является значимым (выбор только двух десятичных значений p-значения без округления), поэтому предположение о однородности нарушается.
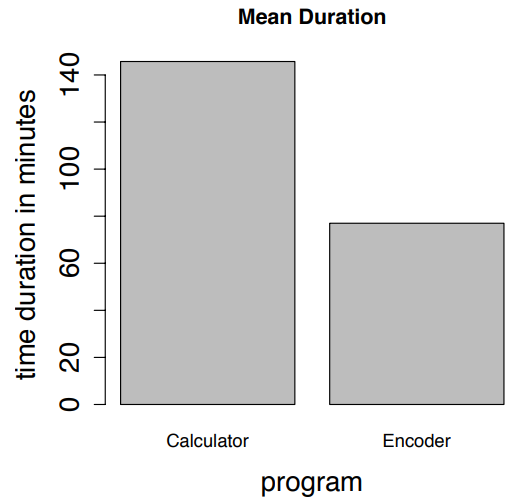
Получив дальнейший анализ, мы обнаружили, что продолжительность написания второй программы была меньше, чем первая. На рис. 1 первая и вторая вертикальные точки данных соответствуют второй программе (Encoder). На рис. 2 показана средняя продолжительность времени для написания обеих программ. Чтобы выполнить это предположение, в будущих экспериментах мы выберем программы с аналогичной сложностью.
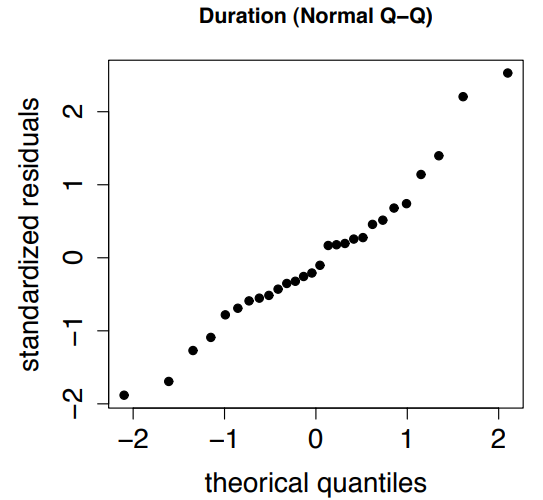
Продолжая следующую оценку предположения, на рис. 3 показан нормальный график вероятности. Если точки (в данном случае стандартизированные остатки) находятся близко к схеме прямой линии, то остатки приблизительно нормальны. Точки, превышающие шаблон прямой линии, соответствуют остаткам, которые больше, чем мы могли бы ожидать от нормальных данных. Точки, которые ниже шаблона прямой линии, соответствуют остаткам, которые меньше, чем мы могли бы ожидать от нормальных данных. Применение теста Колмогорова-Смирнова для нормальности [15, 26] мы получаем значение p 0,8806; Это означает, что мы принимаем нулевую гипотезу в пользу нормальности.
Что касается оценки допущений для усилий, мы получаем аналогичные результаты с теми, которые мы сообщаем о продолжительности; Выполняя тест Левен для однородности дисперсий [17] Мы получаем p-значение 0,0241. Установка альфа -уровня 0,05 этот тест является значительным. Это означает, что отклонения не равны из -за различий между продолжительностью программ. Тест Колмогорова-Смирнова для нормальности [15, 26] дает PValue 0,8059. Это означает, что мы принимаем нулевую гипотезу в пользу нормальности.
Из -за используемого экспериментального дизайна еще одним предположением, которое стоит оценить, является аддитивность. Конструкции эксперимента, которые реализуют блокировку, предполагают, что между обработкой и блоком нет взаимодействия. В этой ситуации говорится, что лечение и блок -эффекты являются аддитивными [16]. Мы проверяем это предположение, используя тест Тьюки на несаддитивность [27]. В таблице 5 показаны результаты этого теста для конструкции латинского квадрата, используемой в эксперименте.
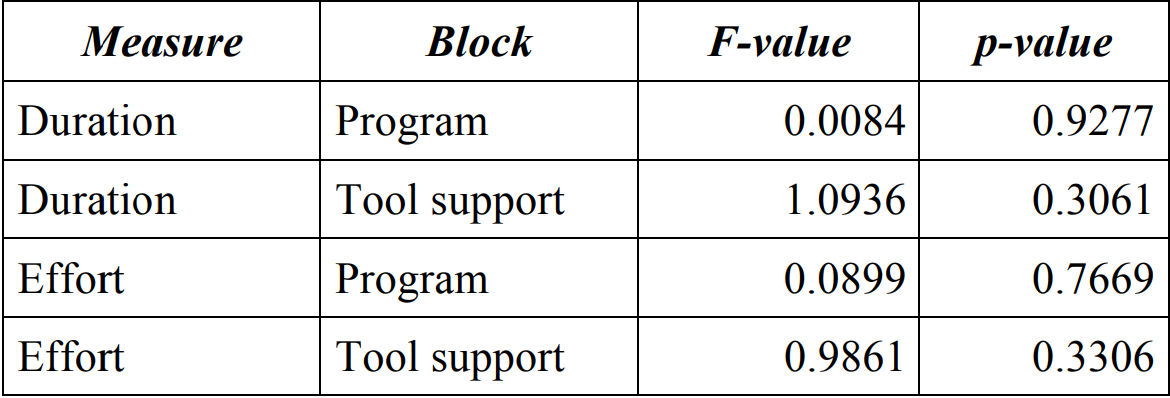
Установка альфа-уровня 0,1 (или меньше), p-значения не являются значимыми. Это означает, что результаты эксперимента удовлетворяют предположению о аддитивности в отсутствии взаимодействия между лечением и блоками.
Авторы:
(1) Омар С. Гомес, профессор программного обеспечения на математическом факультете автономного университета Юкатана (Uady);
(2) Хосе Л. Батун, профессор статистики на штатной статистике на математическом факультете автономного университета Юкатана (Уади);
(3) Рауль А. Агилар, факультет математики, Автономный университет Юкатана Мерида, Юкатан 97119, Мексика.
Эта статья есть
Оригинал
