Изучение локальной и глобальной чувствительности в моделировании бинарных решений
15 июля 2025 г.Таблица ссылок
Аннотация и 1. Введение
Основные помещения для наших моделей
2.1. Как взимаются LLM
2.2 Анедотальная модель из промышленности
2.3 Выбор затрат в модели
2.4 Почему несколько сценариев
Теоретическая модель решения
3.1 Как смоделировать успех
Модель для коммерческих операций на основе одной транзакции
4.1 Пример использования модели
4.2 Анализ модели
4.3 Обсуждение рентабельности рентабельности по сравнению
Моделирование проблемы бинарной классификации
5.1 Локальный анализ чувствительности
5.2 Глобальный анализ чувствительности методом SOBOL
Связанная работа
Будущая работа
Заключение, ссылки и подтверждения
5 Моделирование проблемы бинарной классификации
Проблема бинарной классификации - это тип контролируемой учебной задачи в машинном обучении, где цель состоит в том, чтобы предсказать, к какому из двух классов (категорий) конкретный экземпляр принадлежит [Bishop, 2006]. Выходная переменная в бинарной классификации, как правило, является категориальной переменной с двумя возможными значениями, часто представляемыми как 0 и 1, «да» и «нет», или «истинно» и «false».
Например, в применении медицинской диагностики задача может заключаться в классификации того, имеет ли пациент конкретное заболевание или не основанное на различных входных характеристиках, таких как возраст, артериальное давление, уровень холестерина и другие показатели здоровья.
В контексте бинарной классификации крайне важно понять различные результаты, которые могут возникнуть. Обычно результаты проблем бинарной классификации описаны с помощью матрицы путаницы, в которой перечислены истинные положительные результаты, ложные срабатывания, истинные негативы и ложные негативы [Bishop, 2006].
Истинный положительный (TP) возникает, когда модель правильно предсказывает положительный класс. Например, если модель идентифицирует транзакцию как мошенническую и действительно мошеннической, это истинный позитив. Напротив, истинный отрицательный (TN) возникает, когда модель точно предсказывает отрицательный класс, такой как правильно идентификация нездоровой транзакции [Bishop, 2006].

Затраты, связанные с операцией бинарной классификации, требуют более подробного расчета. Во -первых, это должно быть разделено на то, что будет сделано с каждой операцией. Кроме того, рассматривая только классификацию как истинную или ложную, необходимо учитывать затраты, связанные со всеми возможными вариантами между тем, что делать истинные позитивы, истинные отрицательные, ложные срабатывания и ложные отрицательные.
Сначала интересно проанализировать изменение нашего представительства, чтобы рассмотреть различные затраты.
С этими модификациями ожидаемый доход может быть смоделирован как:

Из уравнения уравнения 30 мы можем рассчитать ROI как:

5.1 Локальный анализ чувствительности
Прямой анализ частичных производных не является абсолютно правильным, потому что существует ограничение, которое:

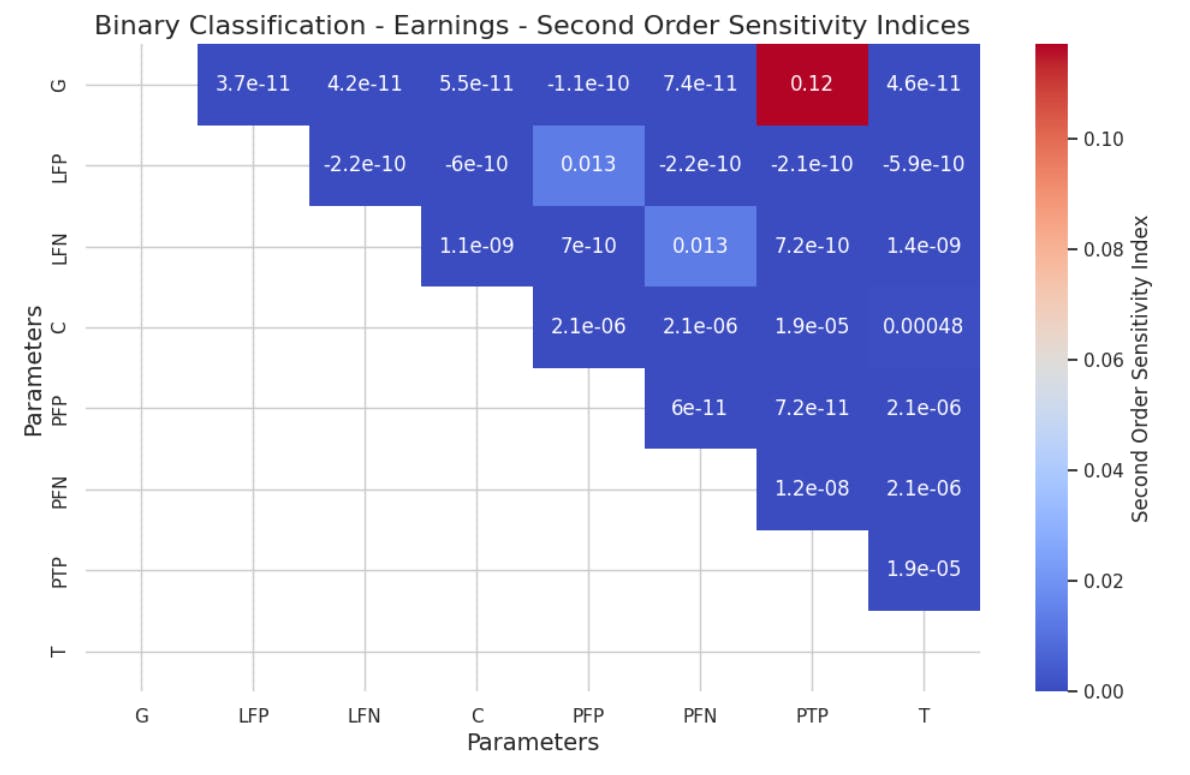
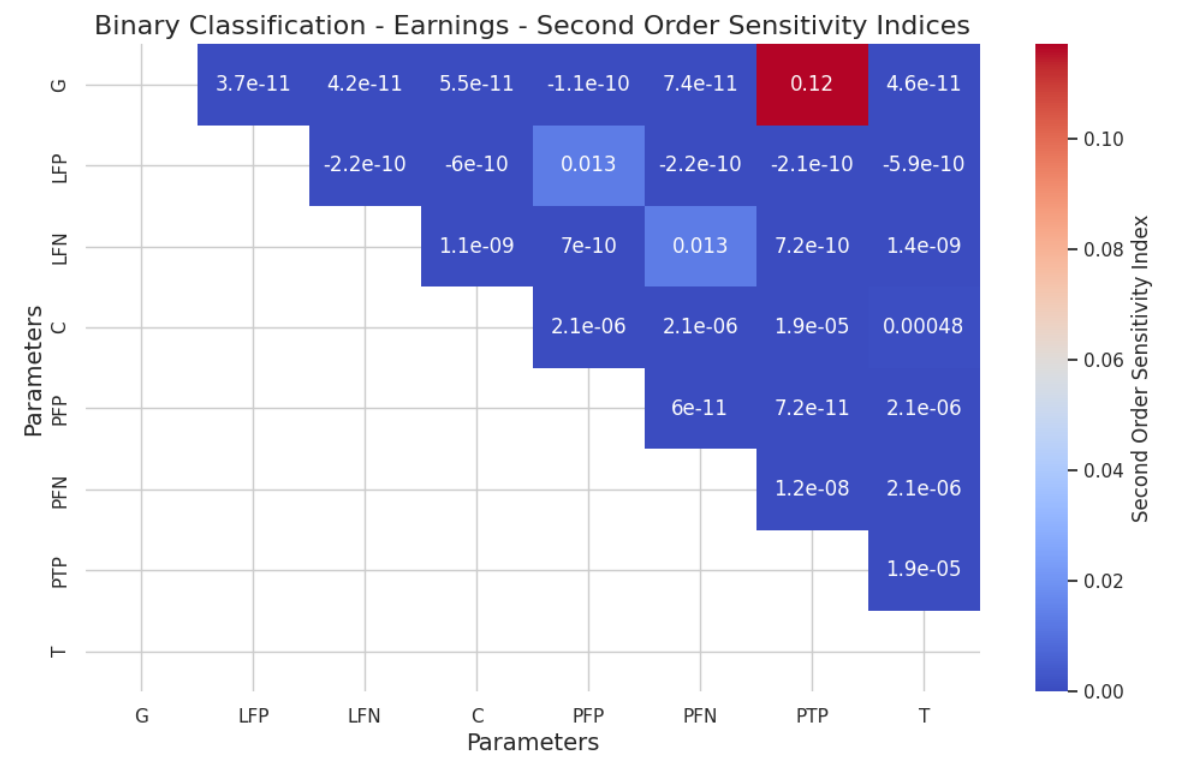
Мы снова проверили матрицу Гессиан, чтобы проанализировать линейность и обнаружили 48 нулей для 64 частичных производных e [e], что является довольно линейным. Тем не менее, опять же, матрица Hessiam для ROI не показывает большого количества нулей, поэтому мы пропустим локальный анализ для ROI.
В уравнениях 41 и 42 есть момент, так как они могут быть переписаны как:

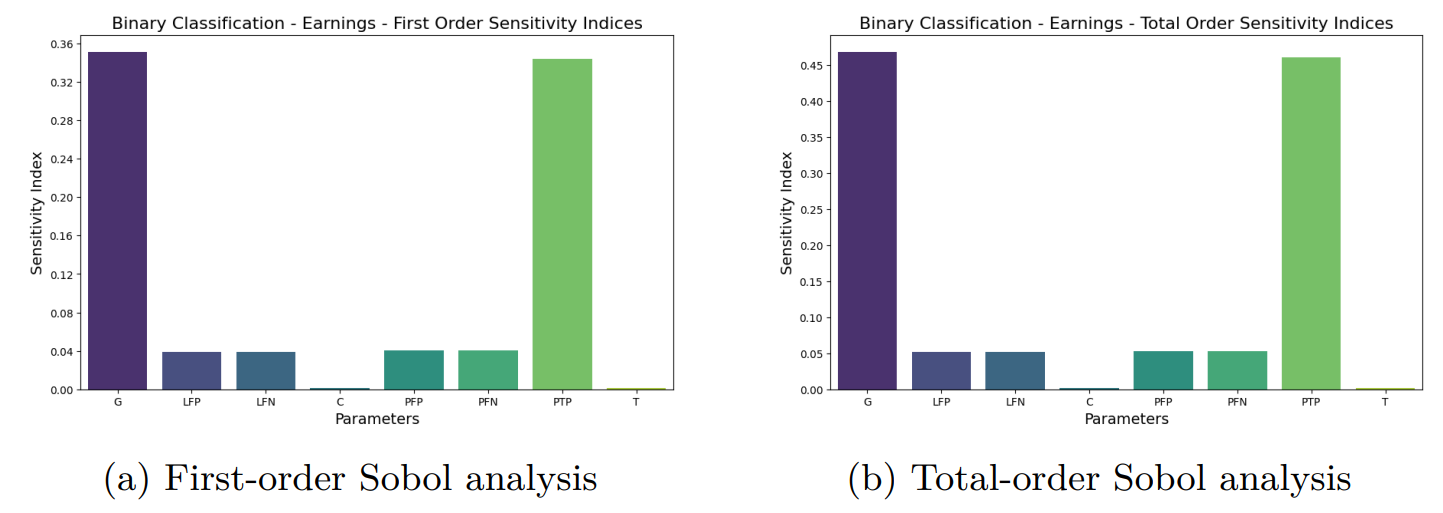
Из этих предыдущих уравнений мы теперь видим разделение влияний: хотя мы использовали только P и (1 - P) в качестве показателей успеха и неудач, существует сильное взаимодействие между P и G + L. Теперь существует разделение, G и различные L в основном влияют на их собственные вероятности происходящих, хотя всегда существует уравнение 32, чтобы показать взаимодействия между вероятностями.
5.2 Глобальный анализ чувствительности методом SOBOL

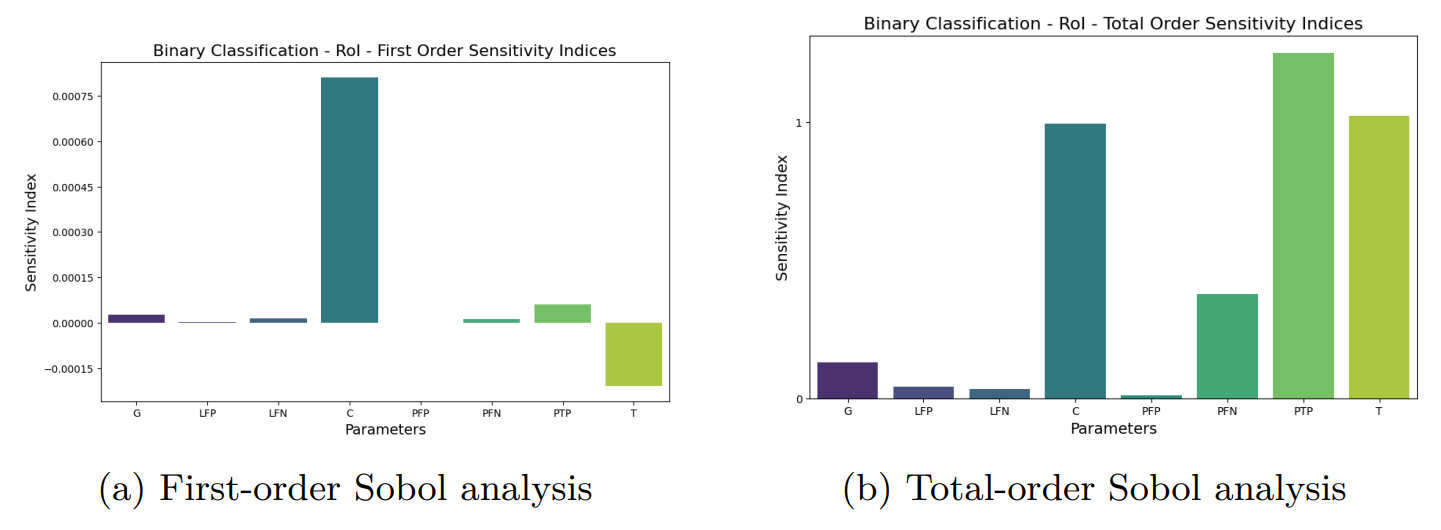
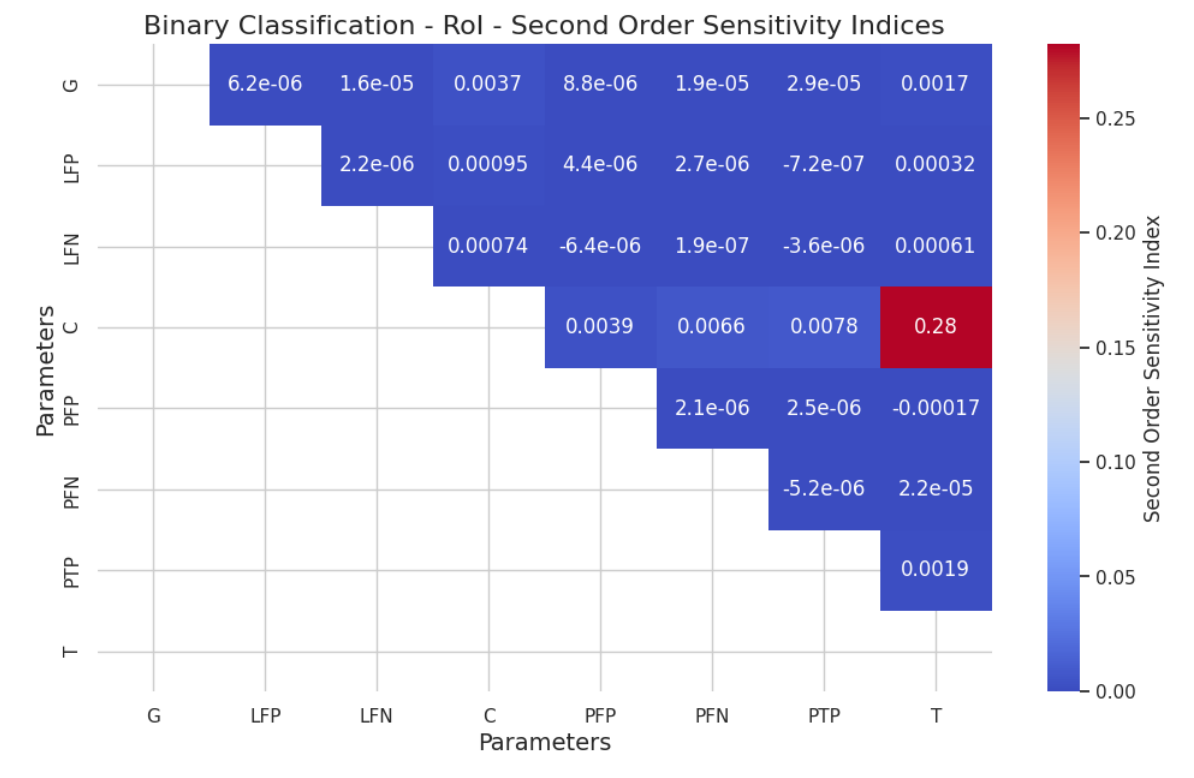
Авторы:
(1) Джеральдо Xexéo, Programa de Engenharia de Sistemas E Computação - Coppe, Universidade Federal Do Rio De Janeiro, Бразиль;
(2) Филипе Брайда, Destamento de Ciência da Computação, Universidade Federal Rural Do Rio de Janeiro;
(3) Маркус Паррейс, Programa de Engenharia de Sistemas e Computação - Coppe, Universidade Federal Do Rio de Janeiro, Бразил и Координадория де Энгенхария де Продушен - Coenp, Cefet/RJ, Unidade Nova Iguaçu;
(4) Пауло Ксавье, Programa de Engenharia de Sistemas E Computação - Coppe, Universidade Federal Do Rio de Janeiro, Бразил.
Эта статья есть
Оригинал
