Выполнение T-теста в Python

Т-тест: самый популярный тест гипотез

В современном мире данные генерируются и потребляются ежедневно. Все эти данные содержат бесчисленное количество скрытых идей и информации, раскрытие которых может быть утомительным. Специалисты по данным обычно подходят к этой проблеме, используя статистику, чтобы делать обоснованные предположения о данных. Любое проверяемое предположение относительно данных называется гипотезой. Проверка гипотезы — это метод статистической проверки, используемый для экспериментальной проверки гипотезы. В науке о данных проверка гипотез проверяет предположения на выборочных данных, чтобы получить представление о большей совокупности данных. .

Проверка гипотез варьируется в зависимости от параметра статистической совокупности, используемого для проверки. Одной из наиболее распространенных проблем в статистике является сравнение средних между двумя совокупностями. Наиболее распространенным подходом к этому является t-тест.

В этой статье мы обсудим этот популярный статистический тест и покажем несколько простых примеров на языке программирования Python.

Что такое Т-тест?

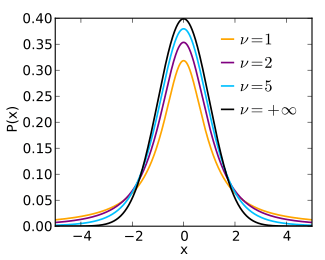
Тест t был разработан Уильямом Сили Госсетом в 1908 году как критерий Стьюдента. Сили опубликовал свою работу под псевдонимом «Студент». Целью этого теста является сравнение средних значений двух связанных или не связанных групп выборок. Он используется при проверке гипотез для проверки применимости предположения к интересующей совокупности.

Т-тесты применимы только к двум группам данных. Если вы хотите сравнить более двух групп, вам придется прибегнуть к другим тестам, таким как ANOVA.

Когда используются Т-тесты?

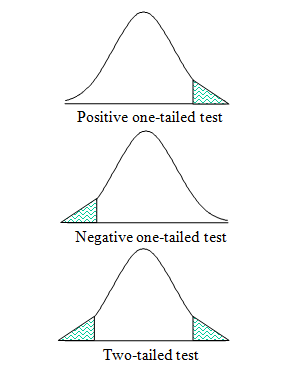
Вместо этого односторонний t-критерий — это направленный критерий, который определяет взаимосвязь между средними значениями совокупности в одном направлении, т. е. в правом или левом хвосте. A двухсторонний t-критерий – это ненаправленный тест, который определяет, существует ли какая-либо связь между средними значениями совокупности в любом направление.

Итак, когда вы ожидаете гипотезу с одним значением, например, среднее1 = среднее2, односторонний тест был бы предпочтительнее. Двусторонний тест имеет больше смысла, если ваша гипотеза предполагает, что средние значения больше или меньше друг друга.

Каковы предположения?

T-тесты – это параметрические тесты для определения корреляции между двумя выборками данных. T-тесты требуют распределения данных в соответствии со следующими предположениями о неизвестных параметрах совокупности:

* Значения данных являются независимыми и непрерывными, т. е. шкала измерения данных должна следовать непрерывному шаблону. * Данные распределены нормально, т. е. при построении их график напоминает колоколообразную кривую. * Данные выбираются случайным образом. * Дисперсия данных в обеих выборочных группах одинакова, т. е. выборки имеют почти одинаковое стандартное отклонение (применимо для двухвыборочного t-критерия).

Какие этапы входят в Т-тесты?

Как и любая проверка гипотез, t-тесты выполняются в следующем порядке:

• Выскажите гипотезу. Гипотеза классифицируется как нулевая гипотеза (H0) и альтернативная гипотеза (Ha), которая отвергает нулевую гипотезу. Нулевая и альтернативная гипотезы определяются в соответствии с типом выполняемого теста.
• Соберите образцы данных.
• Проведите тест.
• Отклонить или не отклонить нулевую гипотезу H0.

Какие параметры используются в Т-тестах?

Помимо групповых средних и стандартных отклонений, в t-критериях есть и другие параметры, которые участвуют в определении достоверности нулевой гипотезы. Ниже приведен список тех параметров, которые будут неоднократно упоминаться при реализации t-тестов:

* T-статистика: t-тест сводит все данные к одному значению, называется t-статистикой. Это единственное значение служит мерой доказательства против заявленной гипотезы. Т-статистика, близкая к нулю, представляет наименьшее свидетельство против гипотезы. Большее значение t-статистики представляет убедительные доказательства против гипотезы. * P-значение: p-значение — это процентная вероятность того, что t -статистика произошла случайно. Он представлен в виде десятичного числа, например, значение p, равное 0,05, представляет 5%-ную вероятность увидеть t-статистику, по крайней мере, столь же экстремальную, как рассчитанная, при условии, что нулевая гипотеза верна. * Уровень значимости: Уровень значимости — это процентная вероятность отклонения истинной нулевой гипотезы. Это также называется альфа.

Какие существуют типы Т-тестов?

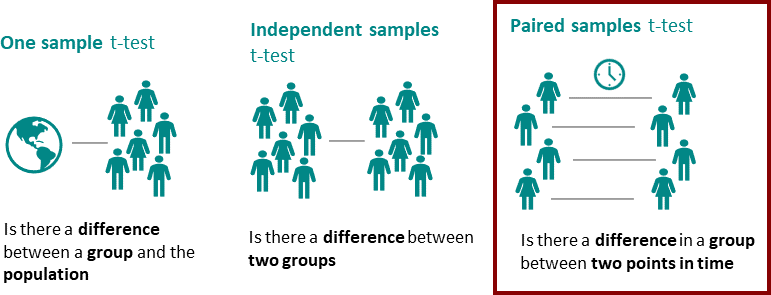
Существует три основных типа t-тестов в зависимости от количества и типа задействованных групп выборки. Давайте углубимся в детали и реализацию каждого типа:

1. T-test с одной выборкой

Одновыборочный t-критерий сравнивает среднее значение группы выборки с гипотетическим средним значением. Этот тест проводится на одной группе образцов, отсюда и название; однообразный тест. Тест направлен на определение того, принадлежит ли группа выборки к гипотетической совокупности.

Формула

t=m-s/n
Where,
t= T-statistic
m= group mean
= preset mean value (theoretical or mean of the population)
s= group standard deviation
n= size of group

Реализация

Шаг 1. Определите гипотезы для теста (нулевые и альтернативные)

Укажите следующие гипотезы:

• Нулевая гипотеза (H0): выборочное среднее (m) меньше гипотетического среднего или равно ему. (<=m)
• Альтернативная гипотеза (Ha): выборочное среднее (m) больше, чем гипотетическое среднее. (>м)

Шаг 2. Импортируйте библиотеки Python

Начните с импорта необходимых библиотек. В Python библиотека статистики используется для t-тестов, которые включают функцию ttest_1samp для выполнения одновыборочного t-теста.

| импортировать numpy как np из scipy; импортировать статистику из numpy.random; |----|

Шаг 3: Создайте случайную группу выборки

Создайте группу случайных выборок из 20 значений, используя функцию normal из библиотеки numpy.random. Установите среднее значение на 150 и стандартное отклонение на 10.

| seed=(1) sample =normal(150,10,20) print('Образец: ', образец) | |----|

Шаг 4. Проведите тест

Используйте функцию ttest_1samp для проведения одновыборочного t-критерия. Установите для параметра popmean значение 155 в соответствии с нулевой гипотезой (выборочное среднее<=среднее значение генеральной совокупности). Эта функция возвращает значение t-statistic и p-значение и по умолчанию выполняет двусторонний тест. Чтобы получить результат одностороннего теста, разделите p-значение на 2 и сравните с уровнем значимости 0,05 (также называемым альфа).

| t_stat, p_value = ttest_1samp(sample, popmean=155) print("Значение T-статистики: ", t_stat) print("P-Value: ", p_value) | |----|

Отрицательное значение t указывает направление экстремума среднего значения выборки и не влияет на разницу между средними значениями выборки и генеральной совокупности.

Шаг 5. Проверка критериев отклонения нулевой гипотезы

Для нулевой гипотезы предполагается, что среднее значение выборки меньше или равно гипотетическому среднему:

• Отклонить нулевую гипотезу, если значение p <= альфа
• Невозможно отклонить нулевую гипотезу, если p-value > альфа
• Отклонить или не отклонить гипотезу на основе результата

Результаты показывают, что p-значение равно 0,21, что больше = 0,05, что не позволяет отвергнуть нулевую гипотезу. Таким образом, этот тест заключает, что среднее значение выборки было меньше гипотетического среднего.

2. Т-тест с двумя выборками

Тест с двумя выборками, также известный как тест с независимыми выборками, сравнивает средние значения двух независимых групп выборок. Стьюдентный критерий для двух выборок предназначен для сравнения средних значений выборок, принадлежащих двум разным совокупностям.

Формула

t=mA- mBs2nA+s2nB
Where,
mA and mB = means of the two samples
nA and nB = sizes of the two samples
s2 = common variance of the two samples

Реализация

Шаг 1. Определите гипотезы (нулевую и альтернативную)

Сформулируйте следующие гипотезы для уровня значимости =0,05:

• Нулевая гипотеза (H0): средние значения независимых выборок (m1 и m2) равны. (m1=m2)
• Альтернативная гипотеза (Ha): средние значения независимых выборок (m1 и m2) не равны. (m1!=m2)

Шаг 2. Импортируйте библиотеки

Начните с импорта необходимых библиотек. Как и ранее, библиотека статистики используется для t-тестов, которые включают функцию ttest_ind для выполнения независимого выборочного t-теста (тест с двумя выборками).

| из numpy.random импортировать семя из numpy.random импортировать randn из numpy.random импортировать нормальный из scipy.stats импортировать ttest_ind | |----|

Шаг 3. Создайте две независимые группы образцов

Использование нормальнойфункции генератора случайных чисел для создания двух нормально распределенных независимых выборок из 50 значений, разных средних значений (30 и 33) и почти одного стандарта отклонения (16 и 18). п

запустить генератор случайных чисел

начальное число(1)

создать две независимые группы образцов

sample1= обычный (30, 16, 50) образец2 = нормальный (33, 18, 50) print('Пример 1: ',sample1) print('Пример 2: ',sample2)

Шаг 4. Проведите тест

Используйте функцию ttest_ind, чтобы провести t-критерий с двумя выборками. Эта функция возвращает значение t-statistic и p-значение.

| t_stat, p_value = ttest_ind(sample1, sample2) print("Значение T-статистики: ", t_stat) print("P-Value: ", p_value) | |----|

Шаг 5. Проверка критериев отклонения нулевой гипотезы

Для нулевой гипотезы при условии, что выборочные средние равны:

• Отклонить нулевую гипотезу, если значение p <= альфа
• Невозможно отклонить нулевую гипотезу, если p-value > альфа
• Отклонить или не отклонить каждую гипотезу в зависимости от результата

Результаты показывают, что значение p равно 0,04, что меньше, чем альфа = 0,05, что отвергает нулевую гипотезу. Таким образом, этот t-критерий для двух выборок показывает, что среднее значение первой выборки больше или меньше среднего значения второй выборки.

3. Парный Т-тест

парный t-тест, а также известный как тест зависимой выборки, сравнивает средние значения двух связанных выборок. Образцы принадлежат к одной и той же совокупности и анализируются в разных условиях, например, в разные моменты времени. Этот тест в основном популярен для экспериментов до и после тестирования, когда образец изучается до и после того, как его условия меняются в ходе эксперимента.

Формула

t=ms/n
Where,
t= T-statistic
m= group mean
s= group standard deviation
n= size of group

Реализация

Шаг 1. Определите гипотезы (нулевую и альтернативную)

Сформулируйте следующие гипотезы для уровня значимости =0,05:

• Нулевая гипотеза (H0): средние зависимые выборки (m1 и m2) равны (m1=m2).
• Альтернативная гипотеза (Ha): средние зависимые выборки (m1 и m2) не равны (m1!=m2)

Шаг 2. Импортируйте библиотеки Python

Начните с импорта необходимых библиотек. Импортируйте функцию ttest_rel из библиотеки статистики, чтобы выполнить зависимый выборочный t-критерий (парный t-критерий).

| из numpy.random импортировать семя из numpy.random импортировать randn из numpy.random импортировать нормальный из scipy.stats импортировать ttest_rel | |----|

Шаг 3. Создайте две зависимые группы образцов

Для простоты используйте те же случайные выборки из двухвыборочной реализации. Мы можем предположить, что образцы взяты из одной и той же совокупности.

запустить генератор случайных чисел

начальное число(1)

создать две зависимые группы образцов

sample1= обычный (30, 16, 50) образец2 = нормальный (33, 18, 50) print('Пример 1: ',sample1) print('Пример 2: ',sample2)

Шаг 4. Проведите тест

Используйте функцию ttest_rel, чтобы провести t-критерий с двумя выборками для двух зависимых/связанных выборок. Эта функция возвращает значение t-statistic и p-значение.

| t_stat, p_value = ttest_rel(sample1, sample2) print("Значение T-статистики: ", t_stat) print("P-Value: ", p_value) | |----|

Шаг 5. Проверка критериев отклонения нулевой гипотезы

Для нулевой гипотезы, предполагающей, что выборочные средние равны:

• Отклонить нулевую гипотезу, если значение p <= альфа
• Невозможно отклонить нулевую гипотезу, если p-value > альфа
• Отклонить или не отклонить гипотезу на основе результата

Результаты показывают значение р 0,05, что равно 0,05, следовательно, нулевая гипотеза отвергается. Таким образом, этот парный t-тест показывает, что среднее значение первой выборки больше или меньше среднего значения второй выборки.

Почему t-тесты полезны при анализе данных?

T-тест — универсальный инструмент. Специалисты по данным используют эти тесты для проверки своих наблюдений за данными и вероятности того, что эти наблюдения верны. Это испытанный и испытанный подход к сравнению наблюдений без дополнительных затрат на вовлечение в анализ всей совокупности данных.

От проверки числа покупок нового продукта до сравнения экономического роста между странами — проверка гипотез является важным статистическим инструментом для бизнеса и одним из самых важных инструментов в арсенале статистика. Везде, где задействованы данные, t-тесты будут играть важную роль в проверке результатов данных.

Также опубликовано здесь