Эллиптическая кривая криптографии: глубокое погружение в ее строительные блоки, реализацию и недостатки

Строительные блоки ECC

Одним из самых мощных типов криптографии, используемых в настоящее время, является криптография на основе эллиптических кривых (ECC). Этот метод используется, в частности, для защиты серверов Cloudflare, на которых в настоящее время размещается большая часть онлайн-контента.

Этот алгоритм отвечает за безопасность всего: от HTTPS-соединений клиентов до передачи данных из одного центра обработки данных в другой. Чтобы доверять этой технологии, возможно, стоит разобраться, почему она так важна в современном мире, и посмотреть, как она работает за кулисами.

Возвращаясь к истории криптографии, мы можем провести различие между классической и современной эпохой. 1977 год можно назвать поворотным. Именно тогда были представлены как алгоритм RSA, так и алгоритмы обмена ключами Диффи-Хеллмана.

Эти алгоритмы были революционными, потому что они представляли и применяли на практике первые жизнеспособные криптографические схемы, в которых безопасность основывалась на теории чисел. Его реализация оказалась полезной даже для защиты связи по сети и предоставления возможности двум сторонам обмениваться данными без обмена общим секретом.

Следовательно, криптография превратилась из безопасной передачи секретных кодовых книг по всему миру в возможность безопасного общения между любыми двумя сторонами, не беспокоясь о том, что третьи стороны прослушивают и ждут обмена ключами.

Этот поворотный момент стал строительным блоком новой концепции, согласно которой ключ, который вы используете для шифрования данных, может быть общедоступным, в то время как ключ, который вы используете для расшифровки, остается закрытым. Фактически, это источник криптографии с открытым ключом.

Это основано на предпосылке, что эти алгоритмы легко обрабатывать в одном направлении, но чрезвычайно трудно отменить и вернуться в другом направлении. Другими словами, мы можем думать об умножении как о простом направлении, тогда как разложение произведения пар умножения на два составляющих его простых числа представляет собой трудное для декодирования направление.

Наиболее изученной и известной криптографической системой с открытым ключом является алгоритм RSA, безопасность которого основана на том факте, что факторинг выполняется медленно, а умножение это факт. Как правило, система шифрования с открытым ключом состоит из двух компонентов: открытого ключа и закрытого ключа. Шифрование работает, беря сообщение и применяя к нему математическую операцию, чтобы получить случайно выглядящее число. Дешифрование берет случайно выглядящее число и применяет другую операцию, чтобы вернуться к исходному числу.

Шифрование с помощью открытого ключа можно отменить только путем расшифровки с помощью закрытого ключа. Поскольку компьютеры плохо обрабатывают произвольно большие числа, мы можем убедиться, что числа, с которыми мы имеем дело, не станут слишком большими, выбрав максимальное число и работая только с меньшими числами из этого установленного порога. Делая это, мы будем обращаться с числами так же, как с числами на аналоговых часах. Любое вычисление, в результате которого получается число, превышающее максимальное, будет преобразовано в число в допустимом диапазоне. Например, в алгоритмах RSA максимальное значение получается путем умножения двух случайных простых чисел.

Открытый и закрытый ключи – это два специально выбранных числа, которые больше нуля и меньше максимального значения, называемые pub и priv. Чтобы зашифровать число, вы умножаете его само на себя pub раз, убедившись, что вы выполняете перенос, когда достигаете максимума. Чтобы расшифровать сообщение, вы умножаете его на priv раз и получаете исходное число.

Звучит удивительно, но это действительно работает. Это свойство было большим прорывом, когда оно было обнаружено.

Чтобы представить сообщение математически, мы должны превратить буквы в числа. Распространенным представлением латинского алфавита является UTF-8. Каждому символу соответствует число.

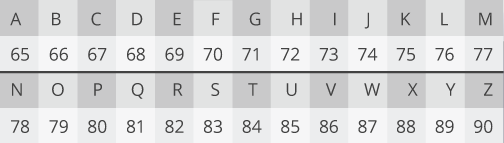
Если мы возьмем в качестве примера слово ОБЛАКО, это приведет нас к числам 67, 76, 79, 85 и 68. Каждая из этих цифр меньше нашего максимального числа 91, поэтому мы можем зашифровать их по отдельности.

Мы должны умножить его на себя 5 раз, чтобы получить зашифрованное значение.

67×67 = 4489 = 30;

Поскольку 4489 больше максимального, мы оборачиваем его, разделив на 91 и взяв остаток.

4489 = 91×41 + 30

30×67 = 2010 = 8

8×67 = 536 = 81

81×67 = 5427 = 58

Это означает, что зашифрованная версия 67 равна 58.

Повторяя процесс для каждого из писем, мы получаем, что зашифрованное сообщение CLOUD становится:

58, 20, 53, 50, 87

Чтобы расшифровать это зашифрованное сообщение, мы берем каждое число и умножаем его само на себя 29 раз:

58 × 58 = 3364 = 88 (помните, что мы делаем цикл, когда число больше max)>

88×58 = 5104 = 8

9×58 = 522 = 67

Вуаля, мы вернулись к 67.

По мере масштабирования эти алгоритмы факторинга становятся более эффективными по мере увеличения размера факторизуемых чисел. Разрыв между сложностью разложения больших чисел на множители и умножения больших чисел сокращается по мере того, как число (то есть длина ключа в битах) становится больше. По мере увеличения ресурсов, доступных для расшифровки чисел, размер ключей должен расти еще быстрее, что является не самыми благоприятными условиями для мобильных и других маломощных устройств с более ограниченной вычислительной мощностью.

Реализация ЕСС

В отличие от факторинга, большинство людей не знакомы с эллиптическими кривыми. Короче говоря, эллиптическая кривая — это набор точек, удовлетворяющих определенному математическому уравнению:

у2 = х3 + ах + б

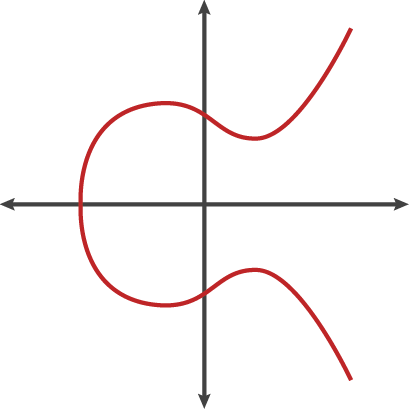
Мы можем наблюдать горизонтальную симметрию:

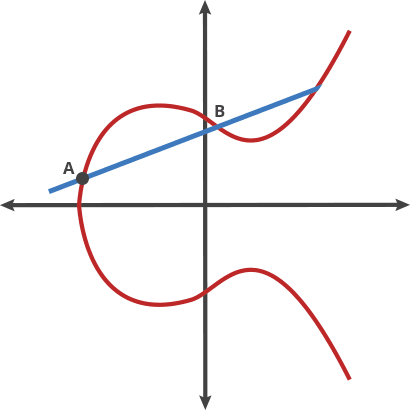
Присмотревшись, мы понимаем, что если мы возьмем любые две точки на кривой и проведем через них прямую, то она пересечет кривую еще ровно в одном месте.

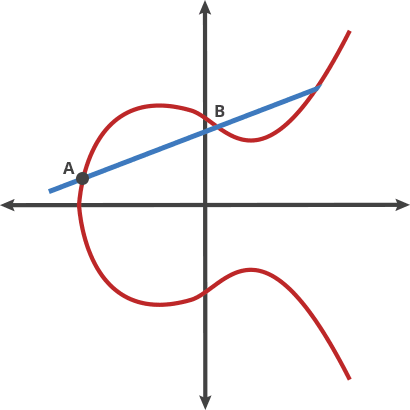
Оказывается, если у вас есть две точки, начальная точка «расставляет точки» сама с собой n раз, чтобы прийти к конечной точке, найти n, когда вы знаете только конечную точку, а первую точку сложно.

Возвращаясь к основам, эту проблему должно быть легко решить и трудно отменить.

Например, представьте, что один человек ударяет по мячу из точки А в точку Б, и когда он попадает в кривую, мяч отскакивает либо прямо вверх, либо прямо вниз на другую сторону кривой.

Если кто-то позже войдет в комнату и увидит, куда попал мяч, то, даже если он знает все правила игры и откуда мяч стартовал, он не сможет определить, сколько раз мяч попал туда, не пробежав через комнату. всю игру снова, пока мяч не окажется в той же точке. Легко сделать, трудно отменить: это основа очень хорошей функции люка.

Приближаемся к более реалистичным целям

Приведенная выше упрощенная игровая динамика не объясняет, как выглядят настоящие криптографические кривые. В действительности эти кривые больше похожи на приведенную ниже. Вот пример кривой (y2 = x3 — x + 1), построенной для всех чисел:

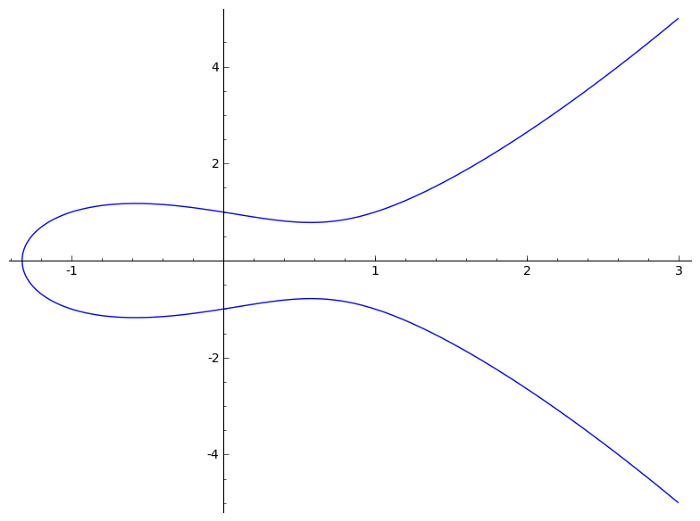
Вот график той же кривой, где представлено только целое число точек с максимальным числом 97:

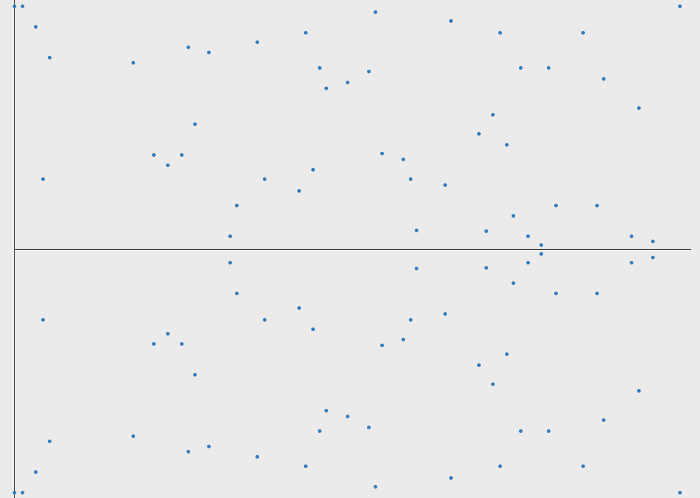
Можно применить такое же упрощенное объяснение. Вы можете визуализировать линию между двумя точками как линию, которая огибает границы до тех пор, пока не будет достигнута определенная точка.

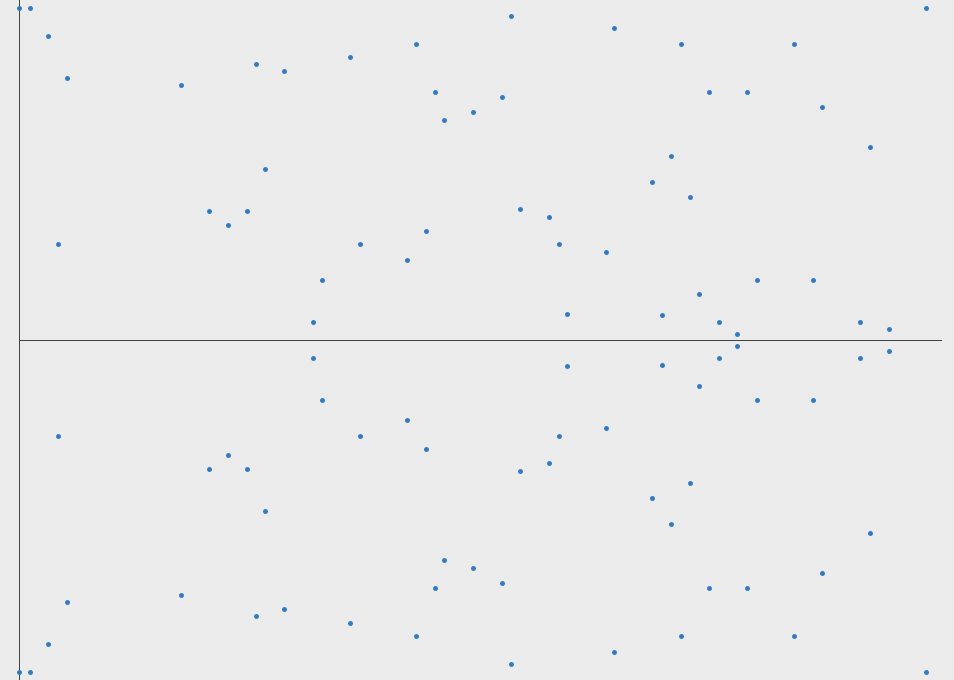
С помощью этого нового представления кривой вы можете брать сообщения и представлять их в виде точек на кривой. Вы можете представить себе, что вы берете сообщение и устанавливаете его как координату x, и вычисляете y, чтобы получить точку на кривой. На практике это немного сложнее, но это общая идея.

Криптосистема на эллиптических кривых может быть определена путем выбора простого числа в качестве максимума, уравнения кривой и общедоступной точки на кривой. Закрытый ключ – это число priv, а открытый ключ – это открытая точка, усеянная самой собой priv раз. Вычисление закрытого ключа из открытого ключа в такой криптосистеме называется функцией дискретного логарифма эллиптической кривой. Оказывается, это функция «люк», которую мы искали.

Приложения в реальном мире

• Подтверждение права собственности

• Анонимность

• Подписи в службах Apple iMessage

• Шифрование DNSCurve

• SSL/TLS-аутентификация

• Идеальная секретность пересылки

Существенный недостаток

• Существует общий скептицизм, связанный с недоверием к самому NIST и стандартам, которые он опубликовал и которые были поддержаны АНБ. Почти все эллиптические кривые попадают под эту угрозу. Несмотря на отсутствие каких-либо известных атак на специальные кривые, они выбраны из-за их арифметической эффективности, и некоторые считают, что широкое внедрение более сложных кривых произойдет через несколько лет. Пока эти нетрадиционные кривые не будут реализованы в браузерах, их нельзя будет использовать для защиты криптографического транспорта в сети.

• Еще одна неопределенность в отношении криптографии на основе эллиптических кривых связана с патентами. BlackBerry владеет более чем 130 патентами, которые касаются конкретных применений эллиптических кривых (благодаря приобретению Certicom в 2009 году). Многие из этих патентов были лицензированы для использования частными организациями и даже АНБ. Это заставило некоторых разработчиков задуматься о том, не нарушают ли их реализации ECC этот портфель патентов.

• Цифровая подпись ECDSA имеет недостаток по сравнению с RSA в том, что она требует хорошего источника энтропии. Без надлежащей случайности закрытый ключ может быть раскрыт.

В заключение отметим, что преимущества ECC по сравнению с традиционным RSA намного перевешивают недостатки. Многие эксперты обеспокоены тем, что математические алгоритмы, лежащие в основе RSA, могут быть нарушены, и ECC останется единственной разумной альтернативой. ECC поддерживается большинством основных браузеров и центров сертификации.