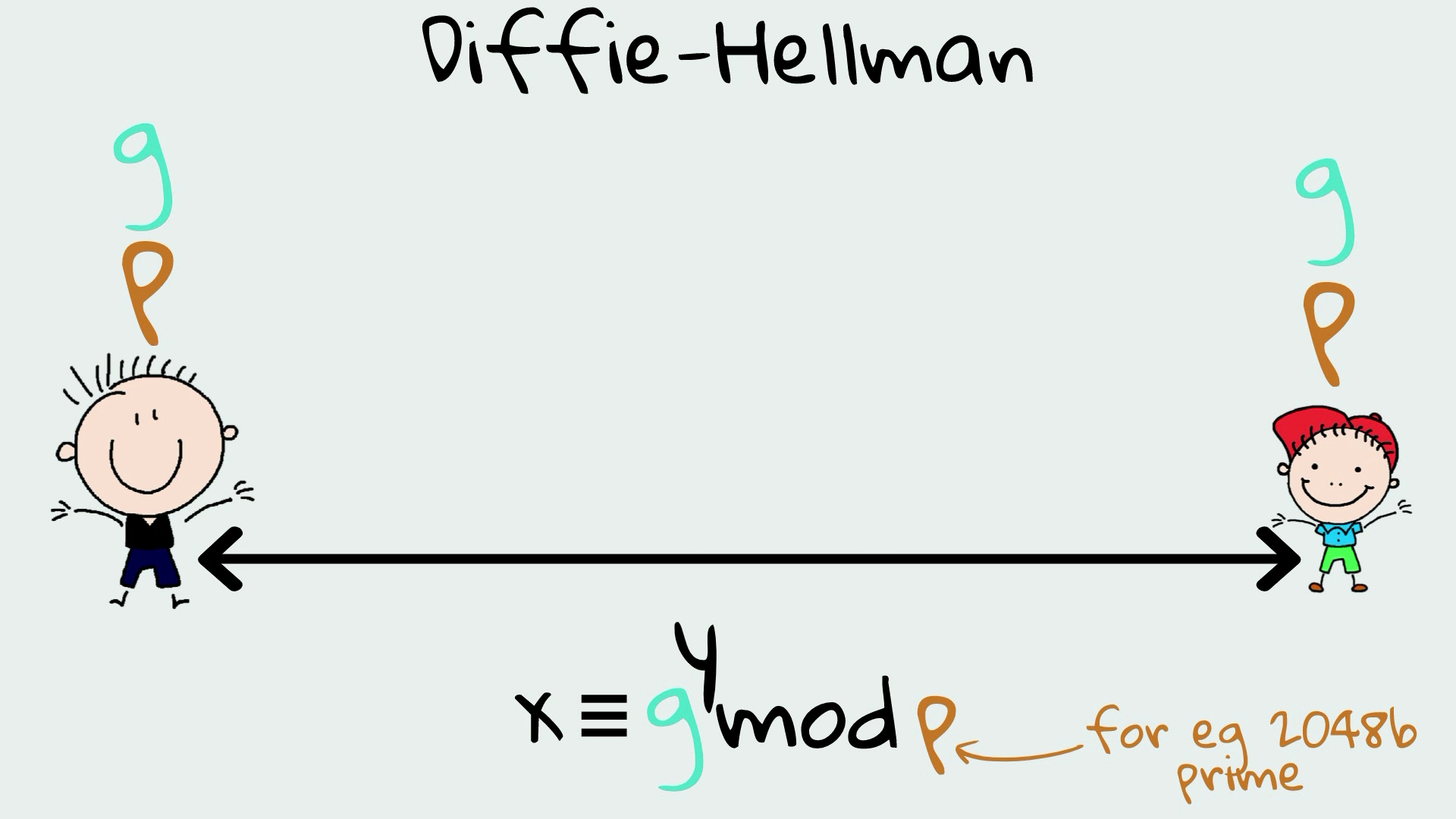
Диффи-Хеллман и его простая математика: краткое объяснение для веб-разработчиков🙆🏻‍♂️
programming web-development javascript tls

Диффи-Хеллман и его простая математика: краткое объяснение для веб-разработчиков🙆🏻‍♂️

22 августа 2023 г.

Смотрите анимационную версию здесь 👇🏻

https://youtu.be/aHSP1bmzqPo?embedable=true

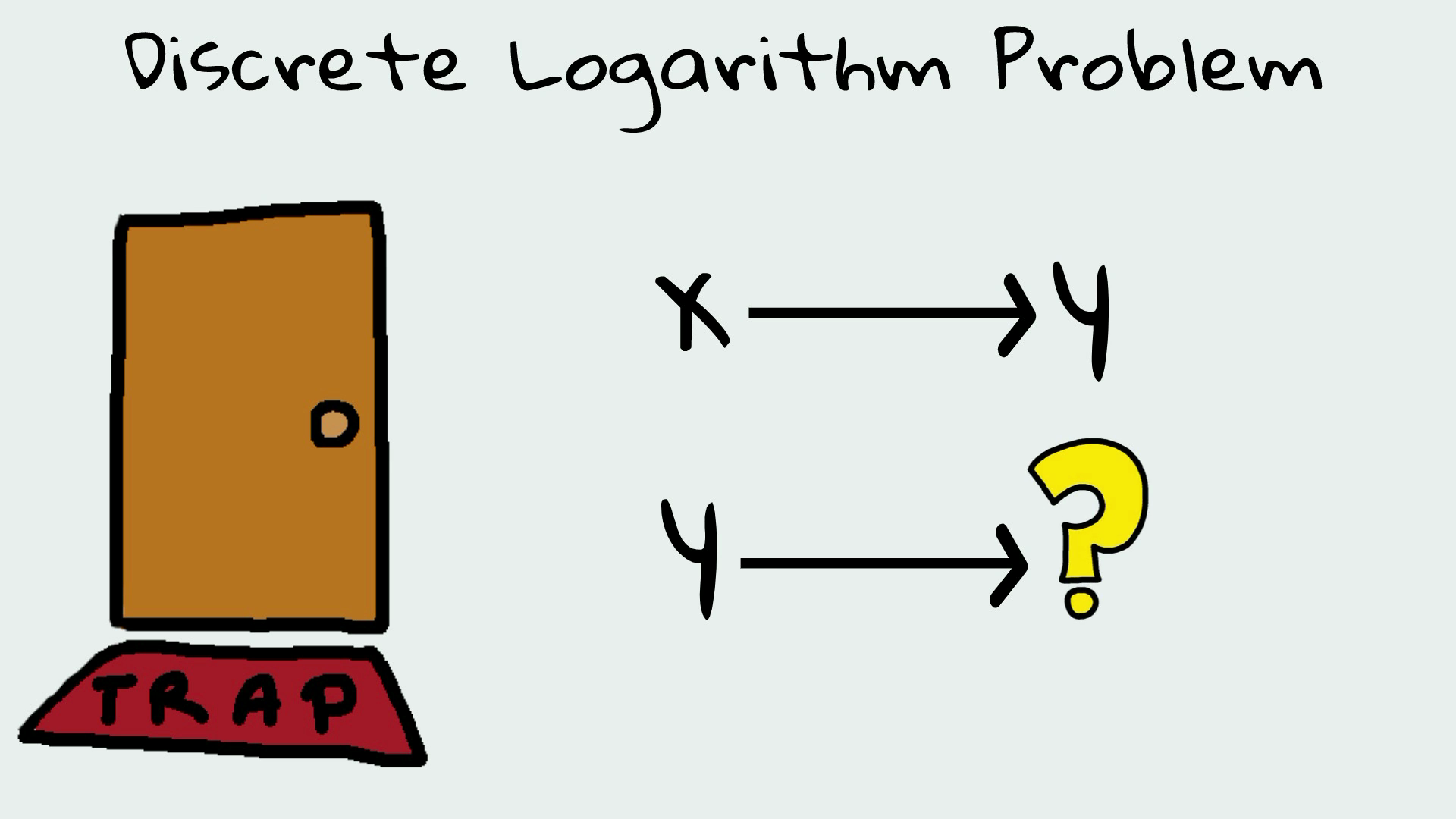
Что такое задача дискретного логарифма?

Чтобы понять алгоритм Диффи-Хеллмана, необходимо разобраться в проблеме дискретного логарифмирования в математике.

Логарифмическая функция соответствует концепции функции с лазейкой.

Функцию-лазейку легко вычислить в одном направлении, но трудно вычислить в противоположном направлении.

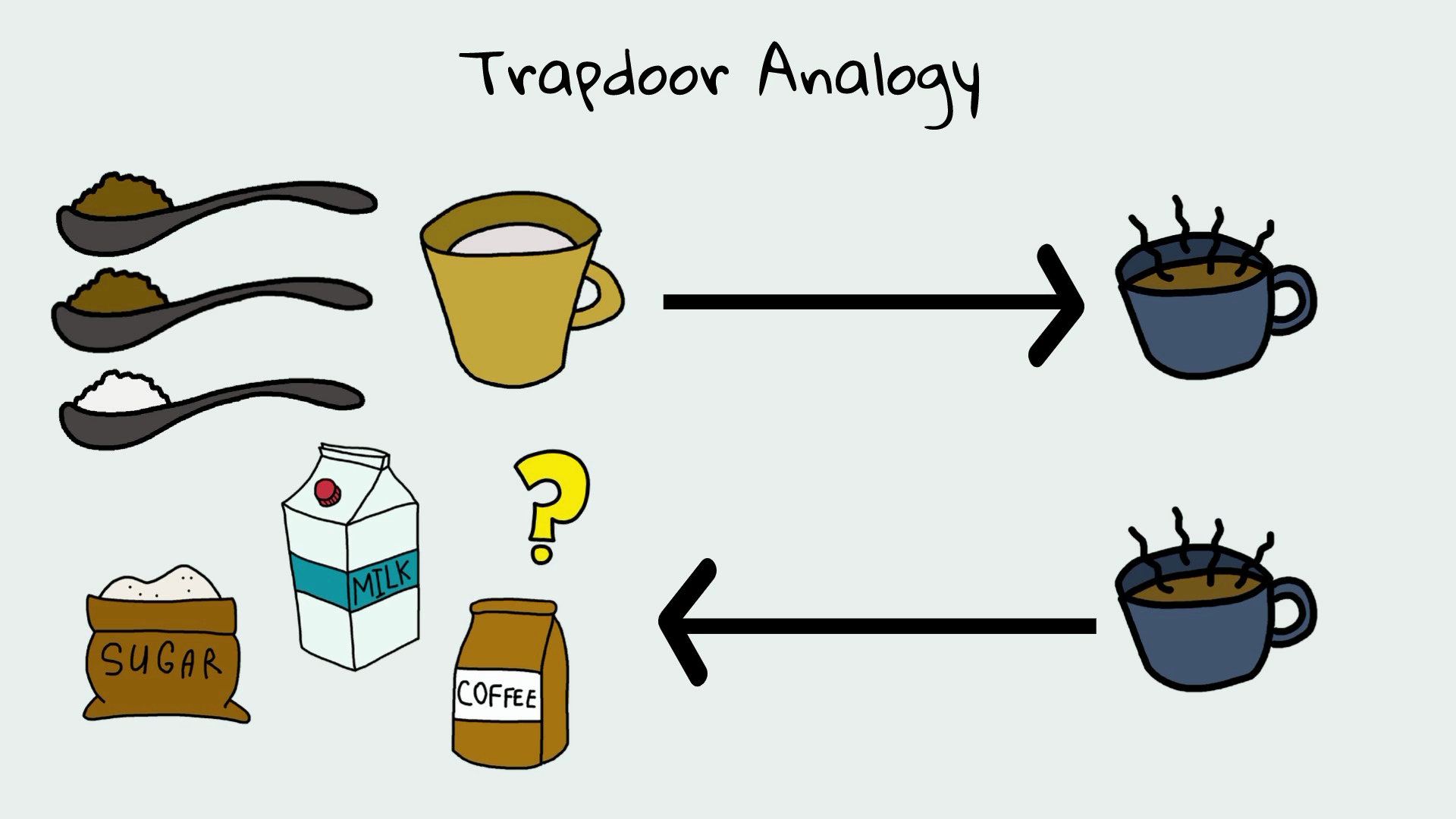
Давайте представим это так:

Из 2 чайных ложек кофе, 1 чайной ложки сахара и полстакана молока можно приготовить кофе.

Теперь, учитывая тот же кофе, сможете ли вы угадать точное количество кофе, сахара и молока?

Операция по модулю

Операция по модулю — это операция, результатом которой является остаток от операции деления, выполняемой с двумя заданными целыми числами в качестве операндов.

Мы говорим 13 по модулю 5 ≡ 3, потому что 13 = 5 x 2 + 3

Что, если мы хотим найти x такой, что 5^x mod 13 ≡ 11?

Давайте попробуем много значений для x и проверим, сколько раз мы найдем ответ.

После 8 попыток мы обнаружим, что для x = 8 получим 5 в степени x mod 13 равно 11

А теперь самое интересное.

Предположим, у нас есть x ≡ g^y mod p.

Но теперь у нас есть p — очень большое простое число (вместо 13), и g и x — тоже очень большие числа (вместо 5 и 11).

И под большими мы подразумеваем действительно большие. Представьте, например, что p эквивалентно 2048 битам:

p=292463028894281219037597349727360684779483317376473239399537257843546320734871513839651347201104480199877191389522614785890996622493775440722572336903336882065975199234931879695261910015161305537526235180562475469982005301778126151856278585195545100903316048416565416635315530213841740854981894053524430751990450476315137696784232893772161407889014577329968174019042697407332291644176957214843165640734510101308586892775505187939228207220238747243895829499434176678189216930154964392995431879145409980273938229601680574417474486982384981120906945098803000392061156847661464691587852166635245652933518718150794527

Можете ли вы найти y, учитывая эти обстоятельства?

Это суть задачи дискретного логарифмирования, и даже с нынешним поколением компьютеров ее решение займет очень много времени. ⌛️

Одна из причин, по которой используются простые числа, заключается в том, чтобы избежать повторяющихся шаблонов

.

Например, возьмем p = 12, не простое число

* 21 мод 12 = 2 * 22 мод 12 = 4 * 23 мод 12 = 8 * 24 mod 12 = 4 (повторяется) * 25 мод 12 = 10 * 26 мод 12 = 2 (повторяется) * 27 мод 12 = 4 (повторяется) * 28 mod 12 = 8 (повторяется)

Например, для p=11 простое число:

  • 21 mod 11 = 2
  • 22 mod 11 = 4
  • 23 mod 11 = 8
  • 24 mod 11 = 5
  • 25 по модулю 11 = 10
  • 26 mod 11 = 9
  • 27 mod 11 = 7
  • 28 mod 11 = 3
  • 29 mod 11 = 6
  • 210mod 11 = 1

Задача дискретного логарифма лежит в основе алгоритма обмена Диффи-Хеллмана.

Диффи-Хеллман

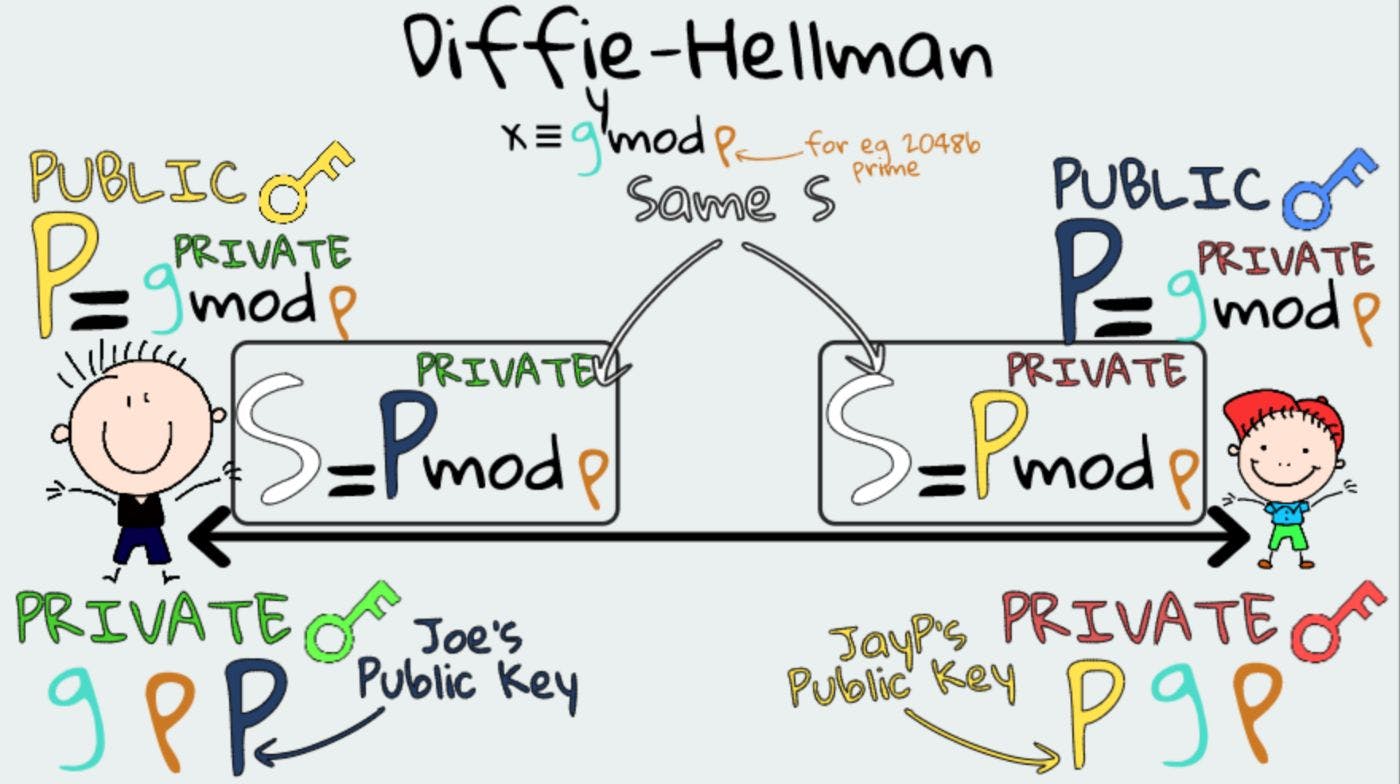
Обмен ключами Диффи-Хеллмана можно использовать для безопасного обмена секретным ключом по незащищенной сети. Он работает с использованием концепции простых чисел и операций по модулю.

Во-первых, JayP и Joe согласны с двумя числами: g и p, большим простым числом. Они будут опубликованы в общедоступном Интернете.

Затем каждый из JayP и Joe создаст случайный закрытый ключ, который не будет передаваться через Интернет.

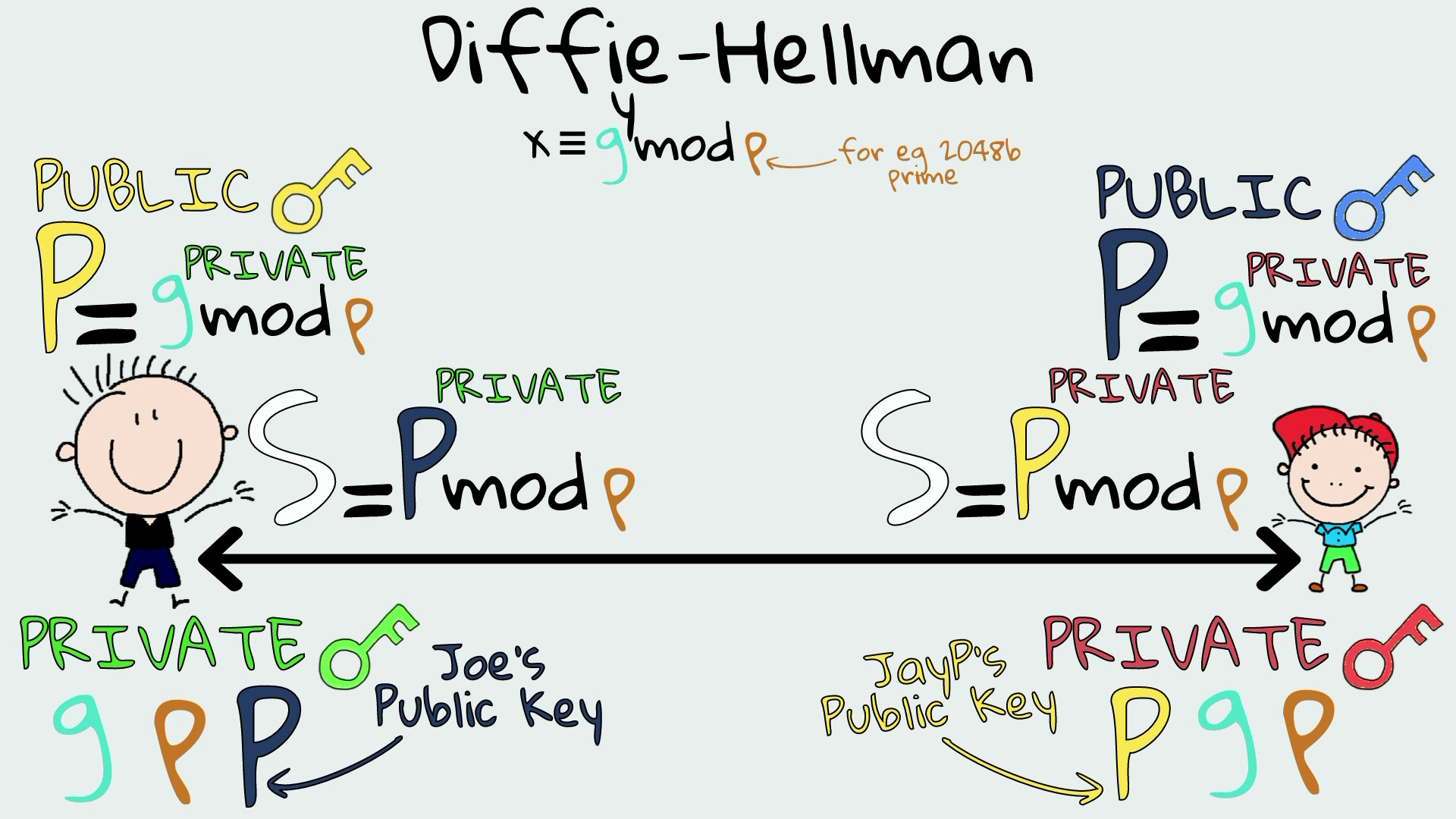
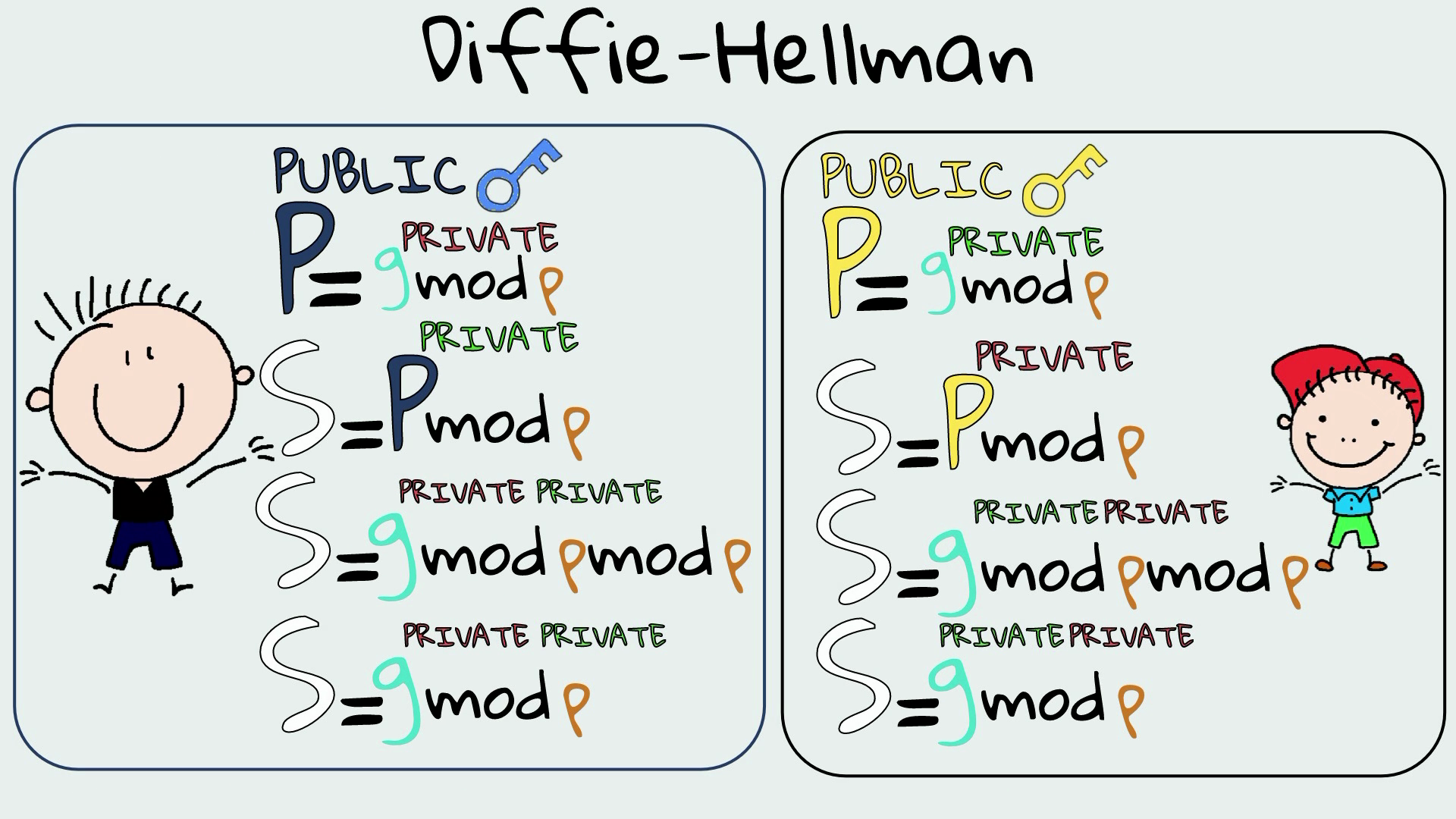
Вычисление открытых ключей 🔑

После этого JayP вычисляет свой открытый ключ по формуле на скриншоте ниже и отправляет его Джо. Точно так же Джо таким же образом вычисляет свой открытый ключ и отправляет его JayP.

Напомним, что до сих пор обе стороны обменивались через общедоступный Интернет параметрами g и p и их соответствующими открытыми ключами. Закрытые ключи не были переданы. Теперь давайте посмотрим, как общий секрет будет получен из этих параметров.

Вычисление секрета 🤫

JayP вычисляет общий секрет на своей стороне, используя уравнение, показанное на снимке экрана ниже.

Джо также вычисляет общий секрет на своей стороне, используя то же уравнение.

Секретный ключ, который каждый из них рассчитывает независимо, будет одним и тем же.

Почему? Ну, из-за простой математики. Применим замену открытых ключей с каждой стороны.

Это объясняет, как ДжейПи и Джо участвуют в создании общего секретного значения, фактически не передавая его.

Безопасность Диффи-Хеллмана 🔐

Зная p, g и y, очень легко вычислить S.

Но в общедоступном Интернете Чейди может видеть только p и g, и ему будет очень сложно вычислить y. Вычисление y — это задача дискретного логарифмирования, о которой мы только что говорили.

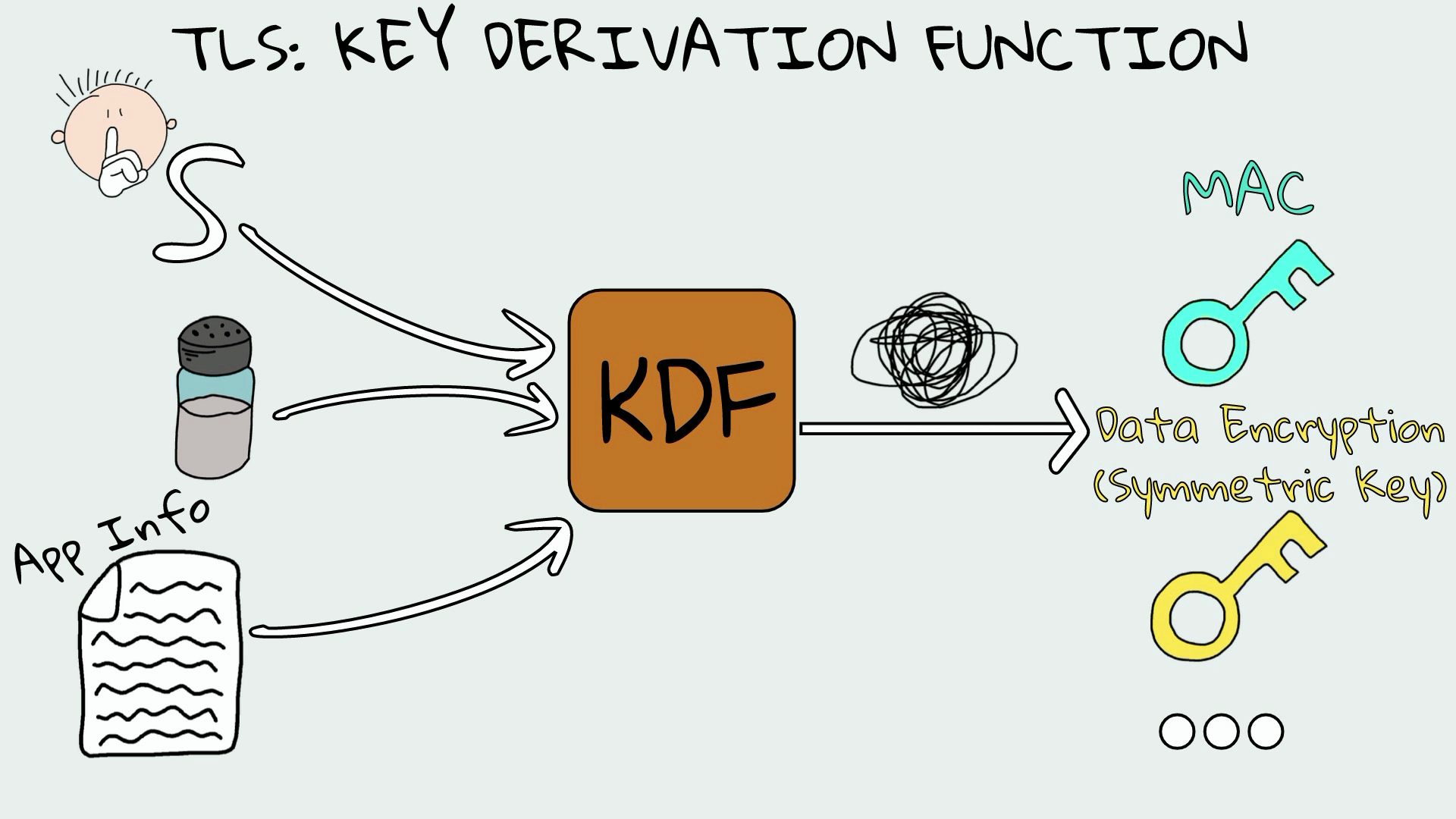
Функция получения ключей

При подтверждении TLS общий секрет будет передан в так называемую функцию получения ключа.

KDF принимает в качестве входных данных общий секрет и другие параметры, такие как соль и некоторую дополнительную информацию о приложении.

Со всеми этими входными данными KDF создаст множество ключей, например, MAC ключ и симметричный ключ, используемый для шифрования данных.

Бесстыдная самореклама 😨

Я запускаю свой новый канал на YouTube, JayPMedia, где я буду делиться всем, что касается веб-разработки. . Если вы хотите учиться и расти вместе со мной, нажмите кнопку подписки, и давайте окунемся в мир программирования и обучения 😉

Также опубликовано здесь:

Оригинал

Recent Post

Categories

PREVIOUS ARTICLE
NEXT ARTICLE