Краткое введение в Python Numpy для начинающих
19 мая 2022 г.NumPy — это библиотека Python, которая в основном используется для работы с массивами. Массив — это набор элементов, которые хранятся рядом друг с другом в памяти. Пока просто думайте о них как о списках Python.
NumPy написан на Python и C. Вычисления в NumPy выполняются частями, написанными на C, что делает их чрезвычайно быстрыми по сравнению с обычным кодом Python.
Установка
Убедитесь, что на вашем компьютере установлены Python и Pip. Затем откройте командную строку или терминал и выполните следующую команду:
``` ударить
пип установить numpy
Создание массивов с помощью NumPy
Вы можете создать массив NumPy, используя функцию array() модуля numpy, как показано ниже:
```питон
импортировать numpy как np
массив = np.массив ([3, 5, 7, 9])
печать (тип (обр))
Вывод будет выглядеть следующим образом:
<класс 'numpy.ndarray'>
Мы только что создали массив NumPy из списка Python. Тип нашей переменной arr — numpy.ndarray. Здесь ndarray означает N-мерный массив.
Измерения или оси в NumPy
В NumPy измерения называются осями (множественное число для оси). Мне нравится думать об оси как о линии, вдоль которой можно хранить элементы.
Простой список или 1-мерный массив можно визуализировать как:
Теперь мы рассмотрим следующее:
- Скаляры (массивы 0D)
- Векторы (одномерные массивы)
- Матрицы (двумерные массивы)
- Трехмерные массивы
- 4D-массивы
Скаляры (массивы 0D)
Скаляр — это всего лишь одно значение.
```питон
импортировать numpy как np
с = np.массив (21)
print("Количество осей:", s.ndim)
печать ("Форма:", s.shape)
Выход:
Количество осей: 0
Форма: ()
Здесь мы использовали 2 свойства массива NumPy:
ndim: возвращает количество измерений (или осей) в массиве. Здесь он возвращает 0, потому что значение само по себе не имеет никаких измерений.
shape: возвращает кортеж, содержащий количество значений по каждой оси массива. Поскольку скаляр имеет 0 осей, он возвращает пустой кортеж.
Векторы (одномерные массивы)
Вектор — это набор значений.
```питон
импортировать numpy как np
vec = np.массив ([-1, 2, 7, 9, 2])
print("Количество осей:", vec.ndim)
печать ("Форма:", vec.shape)
Выход:
Количество осей: 1
Форма: (5,)
vec.shape[0] дает нам количество значений в нашем векторе, которое здесь равно 5.
Матрицы (двумерные массивы)
Матрица — это набор векторов.
```питон
импортировать numpy как np
мат = np.массив([
[1, 2, 3],
[5, 6, 7]
print("Количество осей:", mat.ndim)
печать("Форма:", мат.форма)
Выход:
Количество осей: 2
Форма: (2, 3)
Здесь мы создали матрицу 2x3 (2D-массив), используя список списков. Поскольку матрица имеет 2 оси, кортеж mat.shape содержит два значения: первое значение — количество строк, а второе — количество столбцов.
Каждый элемент (строка) в двумерном массиве представляет собой вектор (одномерный массив).
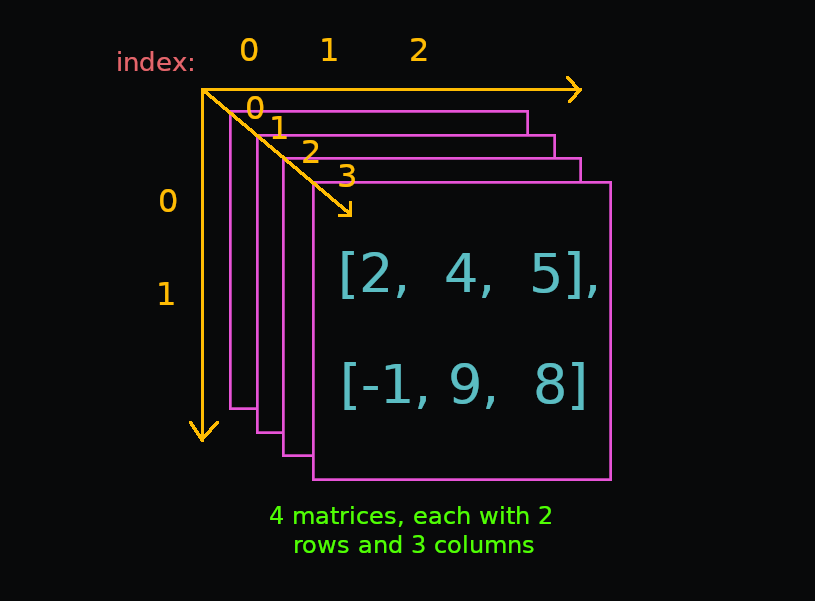
3D-массивы
Трехмерный массив представляет собой набор матриц.
```питон
импортировать numpy как np
т = np.массив ([
[[1, 3, 9],
[7, -6, 2]],
[[2, 3, 5],
[0, -2, -2]],
[[9, 6, 2],
[-7, -3, -12]],
[[2, 4, 5],
[-1, 9, 8]]
print("Количество осей:", t.ndim)
печать ("Форма:", t.shape)
Выход:
Количество осей: 3
Форма: (4, 2, 3)
Здесь мы создали трехмерный массив, используя список из 4 списков, которые сами содержат 2 списка.
Каждый элемент трехмерного массива представляет собой матрицу (одномерный массив). Обратите внимание, что последняя матрица в массиве является самой передней на изображении.
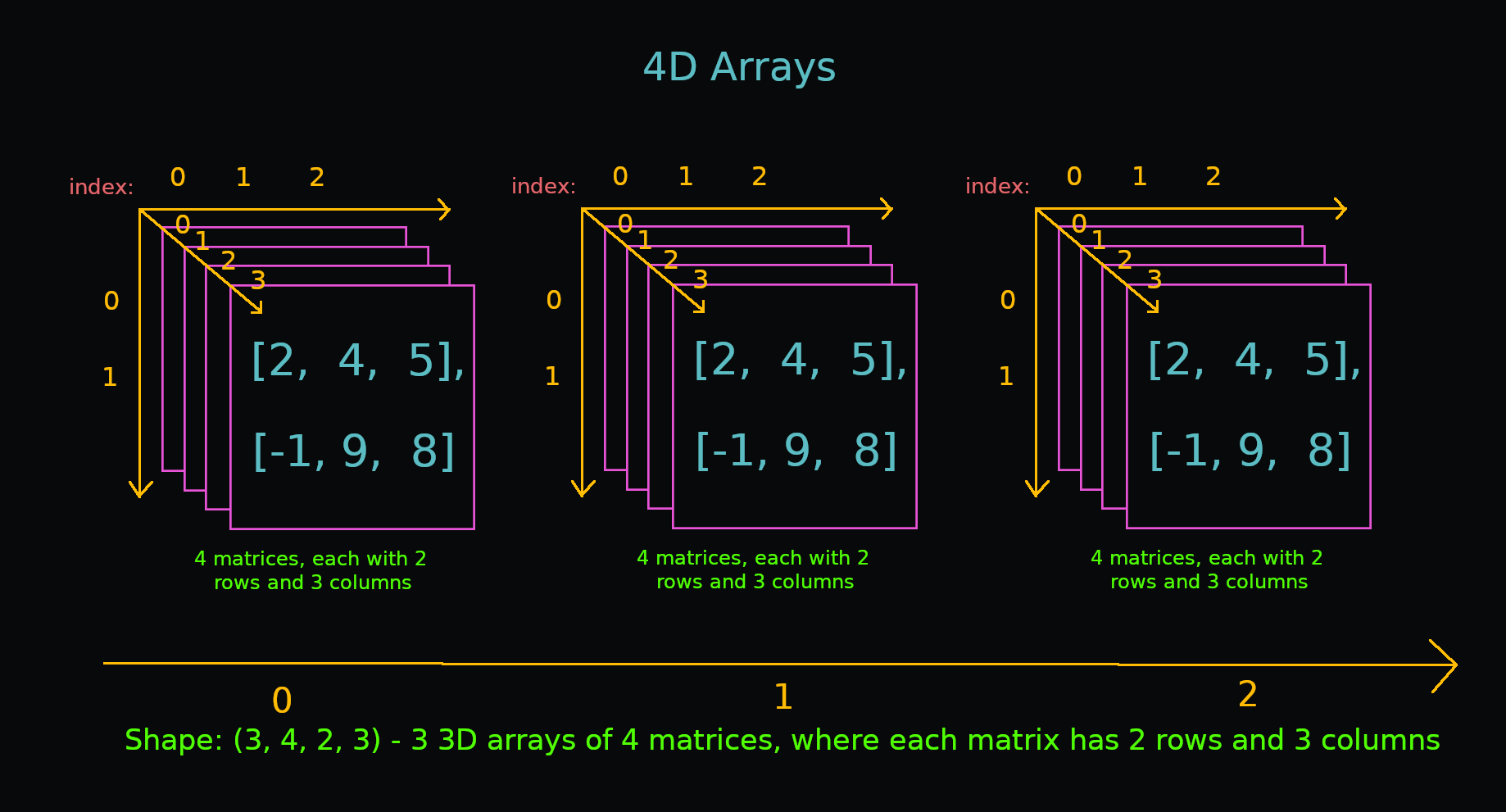
4D-массивы
Посмотрев на приведенные выше примеры, мы видим здесь закономерность. N-мерный массив — это набор n-1-мерных массивов для n > 0. Я надеюсь, что теперь вы лучше понимаете, как визуализировать многомерные массивы.
Доступ к элементам массива
Как и в списках Python, индексы в массивах NumPy начинаются с 0.
```питон
импортировать numpy как np
vec = np.массив ([-3, 4, 6, 9, 8, 3])
print("vec - 4-е значение:", vec[3])
век[3] = 19
print("vec - 4-е значение (изменено):", vec[3])
мат = np.массив([
[2, 4, 6, 8],
[10, 12, 14, 16]
print("мат - 1-я строка:", мат[0])
print("mat - 1-е значение 2-й строки:", mat[1, 0])
print("mat - последнее значение последней строки:", mat[-1, -1])
Выход:
vec - 4-е значение: 9
vec - 4-е значение (изменено): 19
коврик – 1 ряд: [2 4 6 8]
мат - 1-е значение 2-й строки: 10
мат - последнее значение последней строки: 16
Массивы NumPy также поддерживают нарезку:
```питон
продолжение вышеприведенного кода
print("vec - со 2-го по 4-е:", vec[1:4])
print("mat - 1-е строки от 1-го до 3-го значения:", mat[0, 0:3])
print("мат - 2-й столбец:", мат[:, 1])
Выход:
vec - со 2-го по 4-й: [4 6 9]
mat - значения 1-й строки от 1-го до 3-го: [2 4 6]
мат – 2-й столбик: [4 12]
В последнем примере [:, 1] говорит «получить второе значение из всех строк». Следовательно, на выходе мы получаем 2-й столбец матрицы.
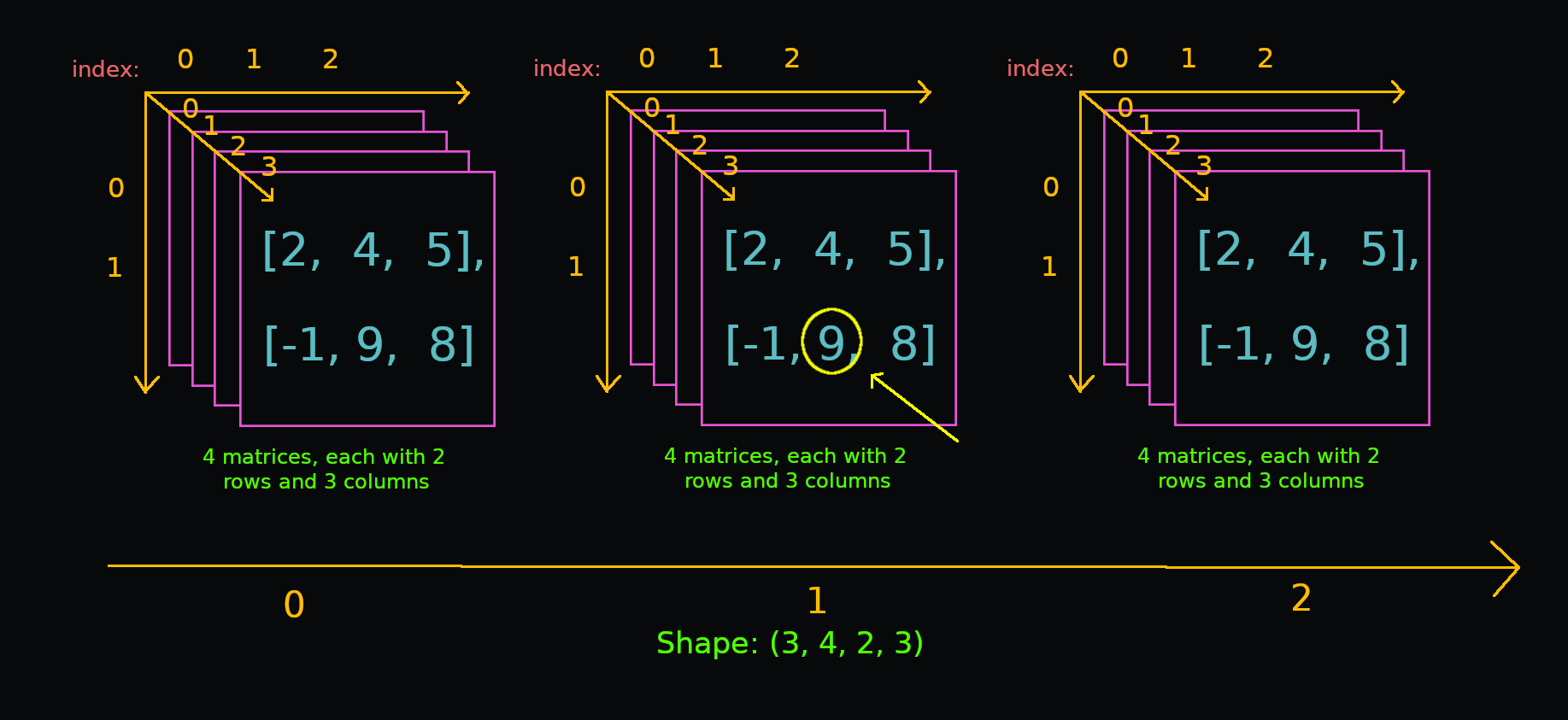
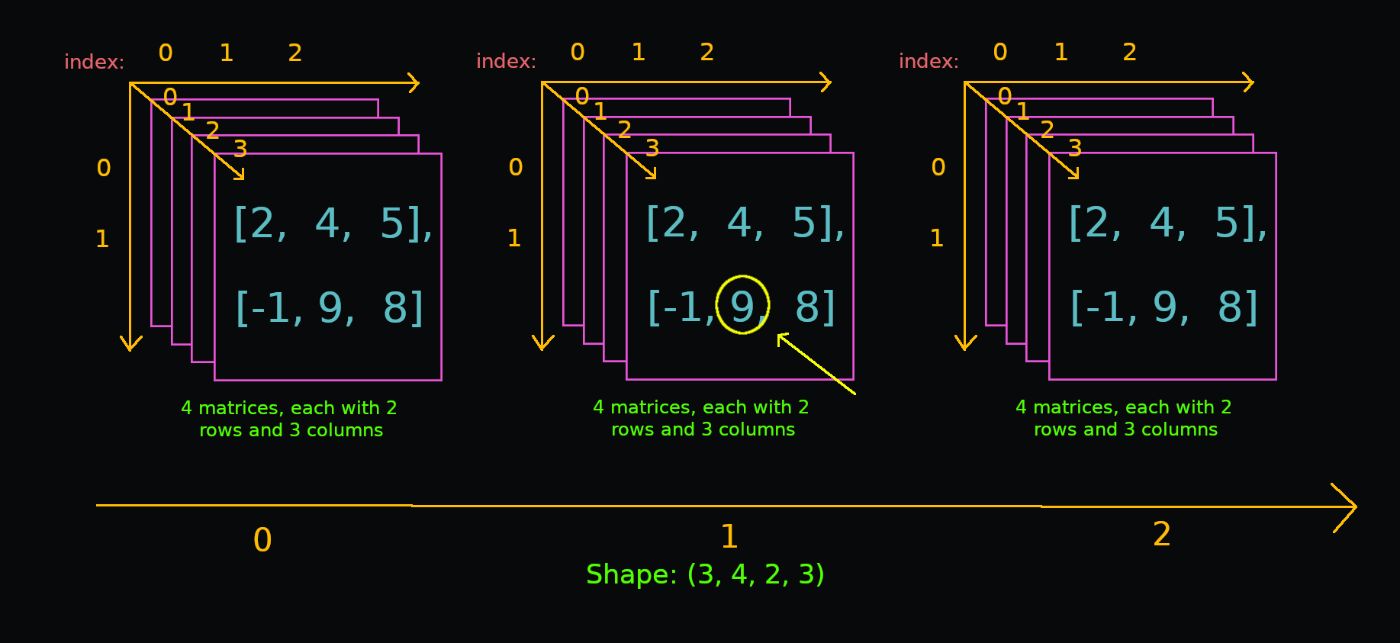
Пример: индексирование в 4D-массиве
Допустим, мы хотим получить доступ к обведенным значениям. Он расположен во 2-м столбце 2-й строки 2-й строки последней матрицы второго трехмерного массива*. Это много, так что не торопитесь.
Вот как получить к нему доступ:
```питон
обр[2, -1, 1, 1]
Python против NumPy
В начале поста я сказал, что вычисления в NumPy выполняются чрезвычайно быстро по сравнению с обычным кодом Python. Давайте посмотрим разницу.
Мы создадим два списка с 10 миллионами чисел от 0 до 9 999 999, добавим их поэлементно и измерим время, которое на это потребуется. Мы преобразуем оба списка в массивы NumPy и сделаем то же самое.
```питон
импортировать numpy как np
время импорта
l1 = список (диапазон (10000000))
l2 = список (диапазон (10000000))
сумма = []
тогда = время.время()
для i в диапазоне (len (l1)):
sum.append(l1[i] + l2[i])
print(f"Только с Python: {time.time() - then: .2f}s")
массив1 = np.массив(l1)
массив2 = np.массив(l2)
тогда = время.время()
сумма = обр1 + обр2
print(f"С NumPy: {time.time() - затем: .2f}s")
Выход:
Только с Python: 2,30 с
С NumPy: 0,14 с
В этом случае NumPy был в 16 раз быстрее, чем необработанный Python.
Оригинал