
Модель для добычи блокчейна в условиях состязания
2 июля 2025 г.Таблица ссылок
Аннотация и 1. Введение
1.1 Связанная работа
Предварительные
2.1 Системная модель
2.2 Цель эгоистичной добычи
2.3 Процессы принятия решений Маркова
Эгоистичная горнодобывающая атака
3.1 Обзор
3.2 Формальная модель
3.3 Формальный анализ
3.4 Ключевые функции и ограничения
Экспериментальная оценка
Заключение, подтверждение и ссылки
A. NAS Mining Цели
B. Системы эффективных доказательств
C. Доказательство теоремы 3.1
2 предварительные
2.1 Системная модель
Мы определяем формальную модель для систем блокчейна, которую мы рассмотрим на протяжении всей этой работы. Модель описывает, как проходит добыча блоков и параметризована несколькими параметрами. Различные значения параметра, затем дают рост формальных моделей для блокчейнов на основе POW, Postake или Post Protocols. Мы предполагаем, что шахтеры в протоколе блокчейна либо состязательны, либо честны. Все честные шахтеры следуют за назначенным протоколом, тогда как состязательные шахтеры работают (то есть ресурсы пула) вместе в коалиции.
Система модели.Мы предполагаем, что добыча блоков проходит в дискретных временных шагах, как во многих моделях POW [17, 24] и Postake [9]. Для майнера, которому принадлежит фракция 𝑝 ∈ [0, 1] общих ресурсов в блокчейне, и которая может добывать до 𝑘> 0 блоков на любом заданном шаге, мы определяем (𝑝, 𝑘)-минимальный следующим образом: вероятность майнинга блока на данном временном шаге пропорциональна 𝑝 · 𝑘, и максимальное число блоков, которые доступны для мономенного монтинг. Можно думать о 𝑘 как о некоторых дополнительных ограничениях на количество блоков, на которых может добывать майнер в любой момент времени, например, Из -за количества VDF, которые они владеют в посте. Следовательно, (𝑝, 1) -ming соответствует майнингу в блокчейнах на основе POW, (𝑝, 𝑘) -mining для 𝑘 <∞ для майнинга в блокчанах на основе пост с 𝑘 VDFS и (𝑝, ∞) -mining для майнинга в блокчейнах на основе почтовой работы.
Состязательная и вещательная модель.Пусть 𝑝 ∈ [0, 1] обозначает долю ресурсов в цепочке, принадлежащей состязательной коалиции. Мы предполагаем, что состязательная коалиция участвует в (𝑝, 𝑘)-Mining, а честные шахтеры участвуют в (1-𝑝, 1)-мининге, где единственное блокирование, которые на шаге честных шахтеров на любое время-самый последний блок в самой длинной общественной цепочке. Когда есть галстук, то есть две самые длинные цепи сплетничают через сеть, честные шахтеры будут добывать в цепочке, которая сначала сплетничится с ними. В таких ситуациях 𝛾 ∈ [0, 1] обозначает вероятность переключения, то есть вероятность того, что честные шахтеры перейдут на цепь противника.
2.2 Цель эгоистичной добычи
Качество цепиПолем Качество цепи является мерой количества честных блоков в любом последовательном сегменте блокчейна. Говорят, что протокол блокчейна удовлетворяет качеству (𝜇, ℓ) -Chain, если для какого-либо сегмента цепи длины ℓ доля честных блоков в этом сегменте, по крайней мере, 𝜇 [16].
Эгоистичная горнодобывающая цель. Пусть 𝜎 обозначает стратегию состязательной добычи. Цель эгоистичной добычи, которую мы анализируем в нашей работе, является ожидаемый относительный доход противника. Формально, пусть Revenuea и доход обозначают количество состязательных и честных блоков в основной цепи соответственно. Ожидаемый относительный доход (Errev) противника в соответствии с стратегией 𝜎 определяется как
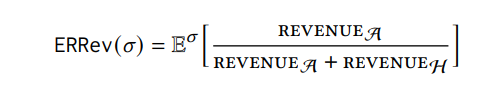
Обратите внимание, что качество цепи блокчейна в рамках стратегии добычи состязания 𝜎 составляет просто 1 - Errev (𝜎), следовательно, наша эгоистичная цель майнинга отражает ожидаемое изменение качества цепи.
2.3 Процессы принятия решений Маркова
Как упомянуто в разделе 1, мы сократим проблему вычисления оптимальных стратегий эгоистичной майнинга для ожидаемого относительного дохода цели по решению MDP с целями среднего платежника. В дальнейшем мы вспоминаем необходимые представления о MDP и формально определяем цели среднего платежа. Для конечного набора 𝑋 мы используем D (𝑋) для обозначения набора всех распределений вероятностей по 𝑋.
Марковский процесс принятия решений.Процесс принятия решений Марков (MDP) [26] - это кортеж M = (𝑆, 𝐴, 𝑃, 𝑠0) где
• 𝑆 является конечным набором состояний, причем 𝑠0 ∈ 𝑆 является начальным состоянием,
• 𝐴 - конечный набор действий, перегруженный для указания для каждого состояния 𝑠 ∈ 𝑆 Набор доступных действий 𝐴 (𝑠) ⊆ 𝐴 и
• 𝑃: 𝑆 × 𝐴 → D (𝑆) - это функция перехода, предписывающая каждому (𝑠, 𝑎) ∈ × × 𝐴 распределение вероятностей по состояниям преемников.
Стратегия в М - это рецепт выбора действия, учитывая историю состояний и действий, то есть это функция 𝜎: (𝑆 × 𝐴) ∗ × 𝑆 → D (𝐴). В целом, стратегия может использовать рандомизацию и память. Позиционная стратегия не использует ни рандомизацию, ни память, то есть это функция 𝜎: 𝑆 → 𝐴. Мы обозначаем по σ и σ 𝑝 набор всех стратегий и всех позиционных стратегий в M. Учитывая стратегию 𝜎, он индуцирует меру вероятности p 𝜎 [·] в M с соответствующим оператором ожидания e 𝜎 [·].
Цель среднего платьяПолем Авознаграждение функцияВ M является функция 𝑟: 𝑆 × 𝐴 × 𝑆 → R, которая для каждого тройного состояния состояния прописывает реальную вознаграждение. Учитывая MDP M, функцию вознаграждения 𝑟 и стратегия 𝜎, мы определяемсредняя платья𝜎 по отношению к 𝑟 через
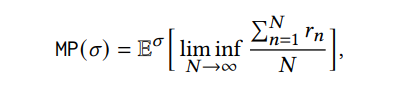
где 𝑟𝑛 = 𝑟𝑛 (𝑠𝑛, 𝑎𝑛, 𝑠𝑛+1) - награда, понесенная на шаге 𝑛.
Проблема MDP средней платы состоит в том, чтобы вычислить максимальную среднюю платежную плату, которую может достичь стратегия в MDP. Классический результат в анализе MDP заключается в том, что всегда существует позиционная стратегия 𝜎 ∗, которая достигает максимального среднего платежа в MDP, то есть 𝜎 ∗ ∈ σ 𝑝 такова, что mp (𝜎 ∗) = max𝜎 ∈σ 𝑝 mp (𝜎) = sup𝜎 ∈σ mp (𝜎 𝜎 𝜎 𝜎 𝜎 𝜎 𝜎 𝜎) [26]. Кроме того, оптимальная позиционная стратегия и средняя плата, которую она достигает, могут быть эффективно рассчитаны в полиномиальное время [15, 26].
Авторы:
(1) Krishnendu Chatterjee, IST Австрия, Австрия (Krishnendu.chatterjee@ist.ac.at);
(2) Амирали Эбрагимзаде, Технологический университет Шарифа, Иран (ebrahimzadeh.amirali@gmail.com);
(3) Мехрдад Карраби, Ист Австрия, Австрия (Mehrdad.karrabi@ist.ac.at);
(4) Krzysztof Pietrzak, IST Австрия, Австрия (Krzysztof.pietrzak@ist.ac.at);
(5) Мишель Йео, Национальный университет Сингапура, Сингапур (mxyeo@nus.edu.sg);
(6) ðorđe žikelić, Сингапурский университет управления, Сингапур (dzikelic@smu.edu.sg).
Эта статья есть
Оригинал
